Логарифмическая линейка

Логарифмическая линейка – устройство, предназначенное для упрощения и ускорения работы с логарифмическими таблицами. Использование логарифмической линейки значительно упрощало операции умножения, деления, возведение в степень, извлечения корня и расчет тригонометрических и логарифмических функций. Различного вида логарифмические линейки широко использовались вплоть до начала восьмидесятых годов, пока небыли вытеснены электронными калькуляторами.

Содержание

1. История создания логарифмической шкалы.

Первую попытку упростить и ускорить работу с логарифмическими таблицами предпринял Эдмунд Гюнтер, профессор астрономии Грэшемского колледжа. Он разработал шкалу, состоящую из нескольких отрезков, располагающихся параллельно на деревянной или медной пластине. На каждый отрезок наносились деления, соответствующие логарифмам чисел или тригонометрических величин.

Рассмотрим пример построения логарифмической шкалы. Возьмем за основу отрезок АВ (рисунок ниже) и примем его за единицу. Следовательно, его можно принять за lg 10, так как lg 10 = 1; Теперь рассчитаем длины отрезков, соответствующих десятичным логарифмам чисел 1,2,…9, c точностью до тысячных долей:

Нанесем эти отрезки на шкалу, учитывая, что отрезок АВ = 1:

Для вычисления с помощью этой шкалы необходимо определить сумму или разность длин от начала шкалы до логарифмов исходных чисел. Далее находим логарифм, соответствующий полученной длине, и по его значению определяем произведение или частное. Например, для умножения 2 на 4 надо сложить длину отрезка для числа 2 (0.301) с длинной отрезка для числа 4 (0.602). Далее находим значение, соответствующее длине отрезка 0.903. Это будет число 8. Таким образом, 2*4 = 8. Обычно такая шкала использовалась вместе с двумя циркулями, позволяющими быстро и точно определять длину результирующего отрезка.

Описание логарифмической шкалы Эдмунд Гюнтер опубликовал в 1620 году, так же в этой книге были опубликованы таблицы логарифмов синусов и котангенсов. Изобретение Гюнтера пользовалось большой популярностью и описывалось во многих книгах. Так, например, описание логарифмической шкалы встречается в книге французского механика Н. Биона «Конструкция и применение математических инструментов», опубликованной в 1723 году. Шкала, описанная в этой книге, имела длину 600 мм и ширину 37. Она состояла из шести частей, предназначавшихся для операций с числами, синусами, тангенсами, синусами-верзусами (sin ver a = 1 – cos a), синусами и тангенсами малых углов, синусами и тангенсами румбов. Так же на шкале предусматривались участки для работы с равномерными величинами – «линия меридиана» и «линия равных частей».

2. История создания логарифмической линейки.

Логарифмическая шкала Гюнтера являлась прародителем логарифмической линейки и подвергалась многократным доработкам. Так в 1624 году Эдмунд Уингейт издал книгу, в которой описал модификацию шкалы Гюнтера, позволяющую легко возводить числа в квадрат и в куб, а также извлекать квадратные и кубические корни. Для этого Уингейт поместил две шкалы, построенные в масштабе 1:2, на одной прямой и три шкалы в масштабе 1:3 – на другой. Перенося с помощью измерительного циркуля отрезки с обычной шкалы на шкалу с масштабом 1:2 или 1:3 и наоборот, можно возводить числа в квадрат или в куб и извлекать квадратные или кубические корни.

Дальнейшие усовершенствования привели к созданию логарифмической линейки, однако, авторство этого изобретения оспаривают два ученых Уильям Отред и Ричард Деламейн.

Впервые о своем изобретении Отред рассказал в 1630 году своему ученику и другу Уильяму Фостеру, учителю математики из Лондона. На тот момент Отред изготовил два типа логарифмических линеек – прямоугольную и круглую. Эти изобретения настолько поразили Фостера, что он уговорил передать ему описание изобретения для последующей публикации.

Осенью этого же года Отред рассказал об изобретении круговой логарифмической линейки своему бывшему ассистенту и учителю математики Ричарду Деламейну, который в ответ на рассказ заявил: «Подобное изобретение сделал и я!» и в этом же 1930ом году опубликовал книгу «Граммелогия, или Математическое кольцо», в которой описал круговую логарифмическую линейку и правила ее использования.

Линейка Деламейна содержала до 13 шкал и состояла из вращающегося внутри кольца круга. Так же на линейке располагался указатель, который передвигался вдоль радиуса, облегчая использование инструмента. В книге так же описывалась методика гравировки таких линеек и способы проверки их точности.

Книга Фостера и Отреда, посвященная описанию круглой логарифмической линейки, была издана в Лондоне только в 1632 году и называлась «Круги пропорций». Линейка, описанная в этой книге, содержала восемь шкал (одна шкала была равномерная, а семь остальных – шкалы логарифмов чисел, синусов и тангенсов), выгравированных на медной пластинке. Для облегчения счета на пластинке закреплялись два указателя (см. рисунок справа).

В следующей книге Фореста «Дополнение к использованию инструмента, называемого Кругами Пропорций», изданной в 1633 году, описывалась прямоугольная логарифмическая линейка Отреда. Она состояла из двух частей, на каждой из которой была нанесена логарифмическая шкала. При вычислении эти части линейки зажимались левой рукой, и правой рукой одна из частей сдвигалась относительно другой.

Авторы логарифмических линеек оспаривали первенство изобретения. Так Деламейн обвинял Отреда в воровстве, утверждая, что он не изобрел круговую линейку, а все сведения о ней почерпнул из его (Деламейна) книги. В ответ на подобные заявления Отред подробно описал историю своего изобретения и заметил, что оно было сделано около 12 лет назад. Кто из них прав так и не удалось выяснить. Видимо придется признать, что изобретение логарифмической линейки было сделано независимо друг от друга Уильямом Отредом и Ричардом Деламейном.

Примерно в те же годы Томасом Брауном была разработана плоская спиральная логарифмическая линейка, позволяющая, благодаря увеличению длины шкалы, повысить точность вычислений. Однако, это изобретение не получило широкой известности и вскоре было забыто. Вновь этот тип логарифмических линеек был изобретен в 1748 году Джорджем Адаме. Линейка Адаме размещалась на медной пластинке диаметром 305 мм и имела 10 витков шкалы.

Примерно 1650 году Милбурн предложил способ увеличения длины шкалы логарифмической линейки путем нанесении спиралевидной шкалы на боковую поверхность цилиндра.

В 1654 году англичанин Роберт Биссакер разработал прямоугольную логарифмическую линейку, состоящую из трех частей длинной 60 см, закрепленных параллельно друг другу. Две внешние части были неподвижно закреплены с помощью медных оправ, а третья (движок) свободно передвигалась между ними. Каждой шкале на неподвижных частях соответствовала аналогичная шкала на движке. Причем шкалы были на обоих сторонах логарифмической линейки.

Независимо от Роберта Биссакера аналогичную структуру линейки разработал в 1657 году Сет Патридж, учитель математике из Лондона.

Следующее усовершенствование линейки произвел Томас Эверард. Во-первых, он применил на практике идеи Уингента, расположив на линейке двойные и тройные шкалы для возведения чисел в квадрат и куб, извлечения квадратного и кубического корней.

Во-вторых, он отметил на шкалах особые точки – числа, наиболее часто встречающиеся при расчетах:

— сторона квадрата, вписанного в круг диаметра 1 (0,707);

— сторона квадрата, равновеликого кругу диаметра 1 (0,886);

— длина окружности с диаметром 1 (3.14);

— объем стандартного галлона вина в кубических дюймах (231);

— объем стандартного бушеля солода (2150,42);

— объем стандартного галлона эля (282).

Основное предназначение линейки Эверарда было определение объема сосудов. Универсальная линейка была разработана в 1779 году Джейсом Уаттом, шотландским изобретателем-механиком.

Джеймс Уатт в то время занимался разработкой паровых машин и для их расчета пользовался логарифмическими шкалами, нанесенными на линейки. Подобные линейки были широко известны, однако, их точность оставляла желать лучшего. Мистер Уатт и мистер Соутерн разработали удобное расположение логарифмических шкал для универсального использования и пригласили опытнейших специалистов своего времени для градуировки первого образца. Копии этого образца были переданы мастерам, работающим над паровой машиной.

В 1850 году девятнадцатилетний французский офицер Амедей Маннхейм создал прямоугольную логарифмическую линейку, ставшую прообразом современных линеек и обеспечивающую точность до трех десятичных знаков. Этот инструмент он описал в книге «Модифицированная вычислительная линейка», изданной в 1851 году. В течение 20-30 лет эта модель выпускалась только во Франции, а затем ее стали изготавливать в Англии, Германии и США. Вскоре линейка Маннхейма завоевала популярность во всем мире.

Логарифмическая линейка долгие годы оставалась самым массовым и доступным прибором индивидуального вычисления, несмотря на бурное развитие вычислительных машин. Естественно, она обладала небольшой точностью и скоростью решения по сравнению с вычислительными машинами, однако, на практике большинство исходных данных были не точные, а приближенные величины, определенные с той или иной степенью точности. А, как известно, результаты вычислений с приближенными числами будут всегда приближенные. Этот факт и высокая стоимость вычислительной техники позволили Логарифмической линейке просуществовать практически до конца 20 столетия.

3. Устройство логарифмической линейки.

Рассмотрим логарифмические линейки, используемые во второй половине 20 века в России. Стандартная логарифмическая линейка состояла из трех, покрытых белым целлулоидом, частей: корпуса (M,N), движка (Q) и бегунка (Б). На корпусе линейки наносилось шесть шкал длиной по 25 см каждая. Длина шкалы в 25 см позволяла получить результаты с точностью до четырех значащих цифр с ошибкой, не превосходящей единицы последнего знака.

На движке так же было нанесено шесть неравномерных шкал длиной 25 см, по три с лицевой и обратной сторон.

Бегунок представлял собой прямоугольную рамку со стеклом, на середине которого нанесена тонкая черта – указатель. Бегунок удерживался на линейке зацепляясь краями рамки. Между бегунком и линейкой устанавливалась пружинка, помогающая свободно перемещаться бегунку и удерживаться ему на линейке.

На обратной стороне линейки приводились справочные данные: математические и физические константы, коэффициенты линейного расширения, модули упругости, удельные веса тел и другие данные.

Рассмотрим назначение шкал линейки.

Шкала А служит для вычисления квадратов чисел, откладываемых на шкале D. Так же можно с помощью шкал А и В вычислять квадратные корни чисел.

Шкала В точно такая же, как шкала А. На этих шкалах нанесены отрезки, пропорциональные (m/2)*lg X. Цена наименьшего деления на участках от 1 до 2, от 2 до 5, от 5 до 10, от 10 до 20, от 20 до 50, от 50 до 100 равна соответственно 0.02, 0.05, 0.1, 0.2, 0.5 и 1.

Шкала L – равномерная. На ней отложены мантиссы (дробная часть десятичного логарифма) логарифмов шкалы D. Наименьшее деление этой шкалы соответствует 0.002, а метки, обозначенные цифрами 1,2,3,4. читаются как 0.1, 0.2, 0.3, 04…

Шкалы D и С называются основными. На них нанесены отрезки, пропорциональные m*lg X, при Х изменяемом от 1 до 10. Значение наименьших делений этих шкал на участке от 1 до 2 означает 0.01, на участке от 2 до 4 они означают 0.02, на участке от 4 до 10 – 0.05.

Шкала R – это шкала обратных значений. Она представляет собой шкалу С (D), но в перевернутом виде. Таким образом, метка 10 этой шкалы будет на левом конце, а 1 – на правом. На этой шкале любой отрезок P от начала шкалы равняется 250-250* lg p = 250* lg (1/p).

Шкалы Sin, S&T и Tg используются при вычислениях с тригонометрическими функциями. Отрезки на этих шкалах пропорциональны следующим функциям:

Для шкалы синусов (Sin): y = k ( lg sin Vs + 1 ),

Для шкалы синусов и тангенсов (S&T): y = k [ lg 1/2( sin V + tg V ) +2],

Для шкалы тангенсов (Tg): y = k ( lg tg Vt + 1 ),

Следует помнить, что каждая метка (риска) на шкалах линейке имеет не одно определенное значение, а всякое другое, которое может быть получено умножением этого значения на 10 в любой степени. То есть, числа … 1525, 152.5, 15.25, 1.525, 0.1525 … будут расположены в одном месте логарифмической линейки.

4. Работа с логарифмической линейкой.

С помощью логарифмической линейки можно производить умножение, деление, возведение в степень и извлечение корней, определять натуральные значения тригонометрических функций заданных углов и по заданным натуральным значениям тригонометрических функций находить соответствующие им углы, определять логарифмы и антилогарифмы чисел, находить логарифмы тригонометрических функций и производить различные вычисления.

Рассмотрим подробно правила выполнения перечисленных выше операций с помощью логарифмической линейки и начнем с умножения и деления.

4.1. Умножение и деление.

Умножение и деление с помощью линейки основывается на свойстве логарифмов:

lg X*Y = lg X + lg Y lg X/Y = lg X – lg Y

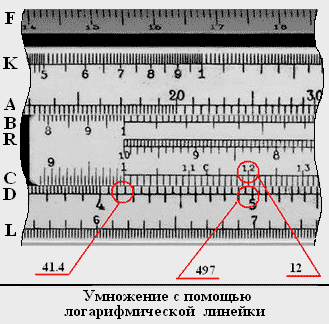
Следовательно, операция умножения сводится к сложению соответствующих отрезков на логарифмических шкалах C и D, а операция деления – к вычитанию этих отрезков. Рассмотрим пример, в котором требуется вычислить X = 41.4 x 12 = 496,8:

1. Ставим указатель бегунка на деление 41.4 на шкале D.

2. Передвигаем движок вправо так, чтобы крайняя левая цифра шкалы C (1) была под указателем бегунка.

3. Ставим указатель бегунка на деление 12 на шкале C.

4. По указателю бегунка считываем число на шкале D (497).

5. Приблизительный результат умножения 497.

Рассмотрим деление на примере y = 5.15/1.31 = 3.931…:

1. Устанавливаем указатель бегунка на деление 5.15 шкалы D.

2. Перемещаем движок логарифмической линейки влево до совпадения указателя бегунка с делением 1.31 шкалы С.

3. Устанавливаем указатель бегунка на левую крайнюю цифру шкалы С (1).

4. По указателю бегунка считываем число на шкале D (393).

5. Приблизительный результат деления будет 3.93.

4.2. Возведение в степень и извлечение корня.

Для возведения в квадрат или в куб числа М устанавливают указатель бегунка на деление шкалы D, соответствующее числу М. По указателю бегунка на шкале А считывают квадрат числа М, а на шкале К – куб числа М. При этом необходимо вручную учитывать порядок результата.

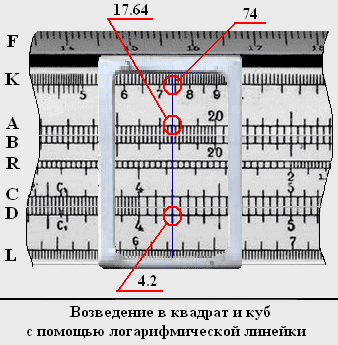
Рассмотрим пример возведения числа 42 в куб и квадрат с помощью логарифмической линейки:

1. Устанавливаем бегунок на деление 4.2 шкалы D.

2. По указанию бегунка считываем число на шкале А (17.64).

4. Приблизительный результат возведения числа 42 в квадрат будет 17.64*10 2 = 1764.

5. По указанию бегунка считываем число на шкале К (74).

6. Определяем порядок результата возведения в куб. В этом случае n = 1, m = 3, следовательно, порядок результата будет 1*3 = 3.

7. Приблизительный результат возведения числа 42 в куб будет 74*10 3 = 74000.

Извлечение корня – действие, обратное возведению в степень, поэтому для того, чтобы извлечь квадратный корень из числа устанавливают указатель бегунка на деление, соответствующее этому числу на шкале А, а результат извлечения смотрят по указателю бегунка на шкале D. Для извлечения кубического корня указатель устанавливают по шкале К, а результат опять же будет на шкале D. Так же, как и при возведении в степень, порядок результата необходимо рассчитывать вручную.

4.3. Работа с логарифмами.

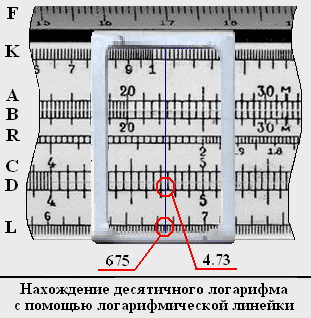
Для нахождении десятичного логарифма числа необходимо указатель бегунка установить на деление шкалы D, соответствующее этому числу. И по указателю бегунка на шкале L определить мантиссу (дробная часть) логарифма. Затем спереди приписать к ней характеристику (целая часть) логарифма. Рассмотрим пример нахождения десятичного логарифма числа 473 (lg 473 = 2.67486…):

1. Устанавливаем указатель бегунка на деление шкалы D, соответствующее числу 473. В нашем случае это будет деление 4.73.

2. Определяем значение мантиссы на шкале L по указателю бегунка (675).

4. Приблизительный результат вычисления десятичного логарифма числа 473 будет 2.675.

Для нахождения числа по заданному десятичному логарифму (потенцирование) устанавливают указатель бегунка на деление шкалы L, соответствующее мантиссе логарифма. По указателю бегунка определяют число, соответствующее мантиссе. Далее вручную определяют порядок результата, исходя из характеристики логарифма.

Рассмотрим пример определения числа, заданного десятичным логарифмом 2.675:

1. Устанавливаем указатель бегунка на деление шкалы L, соответствующее мантиссе заданного десятичного логарифма (675).

2. Определяем по указателю бегунка значение на шкале D (4.73).

4. Приблизительный результат потенцирования: 4.73*10 2 = 473.

4.4. Тригонометрические расчеты.

Логарифмические шкалы Sin, S&T и Tg позволяют производить разнообразные действия над формулами, содержащими тригонометрические функции. Однако, эти шкалы предназначались только для работы с синусами и тангенсами, поэтому при работе с косинусами и котангенсами было необходимо предварительно выразить их через синусы и тангенсы по формулам:

ctg a = 1/tg a, для а от 0 0 до 45 0 ;

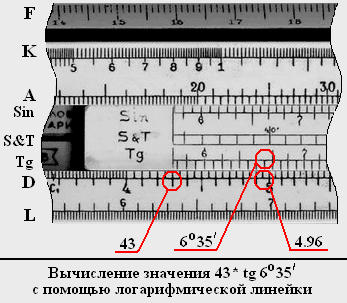
Рассмотрим на примерах методы работы на логарифмической линейке при вычислении тригонометрических функций. Для начала вычислим значение 43*tg6 0 35` = 4.9625…:

1. Устанавливаем указатель бегунка на деление 4.3 шкалы D.

2. Перемещаем движок логарифмической линейки влево до совпадения указателя бегунка с началом шкалы Tg.

3. Устанавливаем указатель бегунка на деление 6 0 35` шкалы Tg.

4. По указателю бегунка считываем ответ со шкалы D. В нашем примере это будет примерно 4.96.

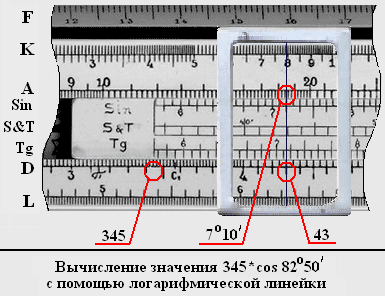
Аналогичные действия необходимо предпринять и при работе с синусами и косинусами. Рассмотрим пример 345*cos 82 0 50` = 43.0408…:

1. Преобразуем косинус в синус: 345*cos 82 0 50` = 345*sin 7 0 10`.

2. Устанавливаем указатель бегунка на деление 3.45 шкалы D.

3. Перемещаем движок логарифмической линейки влево до совпадения указателя бегунка с началом шкалы Sin.

4. Устанавливаем указатель бегунка на деление 7 0 10` шкалы Sin.

5. По указателю бегунка считываем ответ со шкалы D. В нашем случае это будет примерно 43.

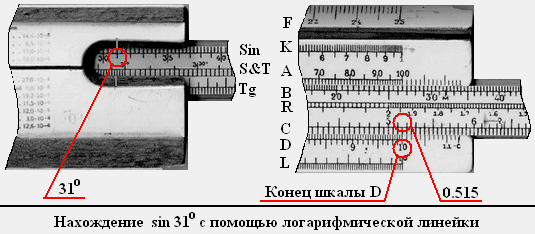
Если же под верхний штрих правого выреза установить, например, 31 0 шкалы Sin, то на шкале С (напротив правого крайнего штриха (цифра 10) шкалы D) будет значение sin 31 0 (примерно 0.515).

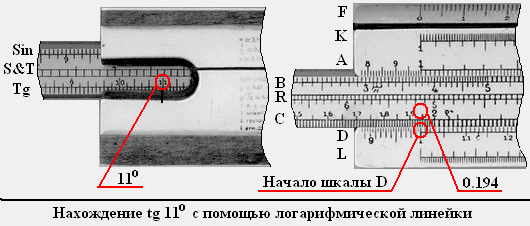
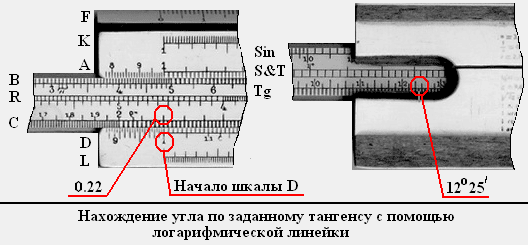
Так же с помощью логарифмической линейки можно находить углы по значениям синуса или тангенса. Рассмотрим пример нахождения угла, которому соответствует tg a = 0.22:

1. Находим на шкале С значение заданного тангенса (0.22).

2. Совмещаем найденное деление шкалы С с началом шкалы D.

Для нахождения угла по заданному синусу (например, sin a = 0.56) совмещаем деление шкалы С, соответствующее синусу (0.56), с концом шкалы D. Переворачиваем линейку и на шкале Sin в правом вырезе напротив верхнего штриха считываем значение искомого угла (примерно 34 0 ).

Стоит помнить, что при определении угла по значению тригонометрической функции, необходимо вручную учитывать в какой четверти находится искомый угол.

Часто при расчетах требуется переводить углы из градусов в радианы. Для этих целей на линейке предусмотрена специальная отметка 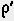. Рассмотрим использование отметки на примере перевода 36 0 12` в радианы:

1. Выражаем заданный угол в минутах (36 0 *60+12` = 2172`).

2. Устанавливаем бегунок на деление 2.172 шкалы D.

3. Подводим под указатель бегунка штрих шкалы С, отмеченный знаком .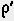

4. Считываем ответ на шкале D напротив конца шкалы C (примерно 0.632 рад).

Рассмотрим перевод угла из радиан в градусы на примере 0.35 рад:

1. Устанавливаем бегунок на деление 3.5 шкалы D.

2. Подводим под указатель бегунка конец шкалы С.

3. Устанавливаем бегунок на деление шкалы С, отмеченное символом .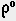

4. По указателю бегунка со шкалы D считываем ответ (примерно 1.2).

5. Ответ считан в минутах без учета порядка. Переведем ответ в градусы и учтем порядок: 1.2/60 = 0.02. С учетом порядка ответ будет примерно 20 градусов.

5. Виды логарифмических линеек.

Часто на логарифмические линейки наносили дополнительные шкалы со значениями функций часто употребляемых на практике, например, в электротехнических, геодезических и других расчетах. Большое распространение имели и дисковые логарифмические линейки. Ниже приведены различные виды логарифмических линеек.

На логарифмических линейках закончим обзор домеханического этапа и перейдем к следующему этапу истории развития ЭВМ – Механическому этапу.

Источник

Линейка логарифмическая – забытое счетное устройство из прошлого?

История создания

Линейкой пользовались аж в древнем мире. Геологи при проведении раскопочных работ на руинах Помпеи нашли деревянные дощечки, внешне очень схожие с обыкновенной линейкой.

В 1793 году Французская Академия приняла за 1 сантиметр сорокамиллионную часть меридиана, проходящего через Париж, а сантиметр разделили на 10 частей, назвав каждую часть — миллиметр. Академики создали эталонный метр из платины. Эталонный метр — это линейка шириной 25 миллиметров, длиной 1 метр, которая является самой точной линейкой и по которой изготавливают другие метрические линейки. Эталонный метр хранится в Международном бюро мер и весов во Франции.

В Россию линейки попали из Франции после Отечественной войны 1812 года. И только в 1899 году по инициативе русского ученого Дмитрия Ивановича Менделеева стали использовать метрическую систему мер, после чего был налажен выпуск линеек.

История логарифмической линейки

Большинство видело логарифмическую линейку (или счётную линейку) только на картинке или в фильмах, таких как «Титаник» (1997 год), «Этот остров Земля» (1955 год) и «Аполлон-13» (1995 год). Если Вы являетесь поклонником «Звёздного пути», то должны знать, что Мистер Спок в нескольких эпизодах пользуется логарифмическими линейками «Jeppesen CSG-1» и «B-1».

Однако было время, когда инженеры ходили не с калькуляторами или мобильными телефонами, а логарифмическими линейками на поясе. Логарифмическая линейка «Pickett» полетела на Луну вместе с космонавтами, а линейка от «K&E» сделала возможным создание атомной бомбы.

Логарифмические линейки являются частью математики и истории. Они не подвержены влиянию электромагнитных импульсов, а, значит, способны пережить Апокалипсис, который нам все пророчат. В случае с логарифмическими линейками, как и многими другими вещами в этой жизни, действует правило: чем больше, тем лучше.

Логарифмическая линейка была разработана английским математиком Уильямом Отредом в XVII веке. Она сохраняла свою популярность среди людей, которые всерьёз занимались математикой, вплоть до начала 1970-х годов. На самом деле идея выполнения различных вычислений при помощи линейки в то врем не была новой.

Ранее Эдмунд Гюнтер разработал сектор с таким же делением, как и у логарифмической линейки, но чтобы с помощью него решить какую-либо проблему, Вам необходим был отдельный набор делительных циркулей. Прибор Отреда представлял собой круговую логарифмическую линейку. Один из его учеников, Ричард Деламейн, утверждал, что также изобрёл логарифмическую линейку. Оба мужчины обвиняли друг друга в воровстве идей.

Современные учёные считают, что они одновременно создали круговую логарифмическую линейку. Деламейн первым публично сообщил о своём изобретении, однако Отред, по всей видимости, завершил разработку логарифмической линейки раньше, чем его ученик.
Обычная логарифмическая линейка была создана Отредом примерно в 1650 году.

Теория логарифмической линейки

Логарифмические линейки связаны с открытием логарифмов Непером. Логарифмы играли важную роль в мире докомпьютерной математики. Давайте рассмотрим в качестве примера десятичный логарифм. Если 10 возвести в квадрат, получится 100. Следовательно, логарифм 100 равен 2. Если Вы возведёте 10 в пятую степень, то получите 100000. Отсюда, логарифм 100000 равен 5. Полученные цифры не обязательно должны быть целыми числами. Так, к примеру, логарифм 200 равен 2,3.

Таблица логарифмов

Если бы Вы тратили много времени на вычисления, то непременно создали бы таблицу чисел и их логарифмов. Вопрос: зачем? Ответ простой. Предположим, Вы захотели умножить два числа – 200 и 100. Это достаточно просто сделать, не прибегая ко всяким хитростям. Вы записываете на листке бумаги «200×100» и умножаете каждую цифру. При помощи логарифмов сделать это намного легче.

Логарифм 200 равен 2,301, а логарифм 100 – 2. Сумма логарифмов 200 и 100 составляет 4,301 (2,301+2). Если Вы возведёте 10 в степень 4,3, то получите не совсем точный ответ (19998,6), поскольку мы округлили логарифм 200. Очевидно, чем больше цифр в Вашей таблице, тем лучше.

Это не совсем удачный пример. Но если Вам нужно умножить 7329 на 8115, то зная логарифмы этих чисел (3,8650 и 3,9093 соответственно), выполнить данное вычисление Вам будет очень легко. Возведите 10 в степень 7,7743, и Вы узнаете правильный ответ – 59470282 (на самом деле 59474835, но, опять же, очень близко).

Подвижные таблицы

Каким образом это связано с логарифмической линейкой? Логарифмическая линейка представляет собой эффективную таблицу логарифмов, выполненную из дерева, пластика или металла. Отметки наносятся на поверхность на основании логарифма числа, однако обозначаются реальными цифрами, то есть расстояние между 0 и 1, к примеру, намного больше, чем расстояние между 8 и 9.

Давайте рассмотрим принцип пользования логарифмической линейкой на простом примере: 2×3. Сдвиньте шкалу С таким образом, чтобы единица оказалась над цифрой 2 на фиксированной шкале D.

Если Вы имеете дело с большими числами, сначала уменьшите их в n-ное количество десятков раз, а после мысленно увеличьте во столько же полученный результат. К примеру, чтобы вычислить произведение чисел 20 и 30, Вам необходимо сначала уменьшить их в 10 раз, а после в 100 раз увеличить полученный результат.

Деление и прочие операции

Деление работает почти так же, однако основано на вычитании. Если Вы сдвинете шкалу С таким образом, чтобы цифра 3 оказалась над 6 на фиксированной шкале D, то сможете под 1 на шкале С увидеть ответ 2 (шкала D). Не запутаться в числах Вам поможет прозрачный пластиковый движок с тонкой линией посередине. В некоторых линейках даже есть небольшое увеличительное стекло, позволяющее лучше рассмотреть отметки на шкале.

Получение правильного ответа

В отличие от калькулятора, логарифмическая линейка, как правило, требует, чтобы Вы имели некоторое представление об ответе, чтобы интерпретировать результаты. Также Вы должны быть в состоянии увидеть разницу между, скажем, 7,3, 7,35 и 7,351. Вот почему чем больше, тем лучше.

Обычная логарифмическая линейка имеет длину около 25 сантиметров. Карманные линейки были короткими, но непрактичными. Также существовали огромные логарифмические линейки, предназначенные для использования в классе (длина некоторых из них достигала 2 метров 15 сантиметров). Для более точных вычислений инженеры пользовались линейками, по форме напоминающими цилиндр. Они были эквивалентом логарифмических линеек длиной до 10 метров.

Выше изображена логарифмическая линейка Отиса Кинга, которая соответствовала линейке длиной 170 сантиметров, однако легко умещалась в кармане. С виду она очень похожа на телескоп. На самом же деле это логарифмическая линейка со шкалой, нанесённой по спирали вокруг инструмента. На линейке Отиса Кинга было больше цифр, чем на обычной логарифмической линейке, однако вычисления, производимые с её помощью, зачастую оказывались не совсем точными.

Как начать коллекционировать логарифмические линейки и где их взять?

Многие думают, что логарифмические линейки трудно коллекционировать, однако на самом деле это довольно легко и недорого. В своё время они были широко распространены, однако после изобретения калькулятора и компьютера вмиг стали никому не нужны. Если постараться, то можно найти людей, у которых сохранились бывшие в употреблении или абсолютно новые логарифмические линейки.

Сайт eBay – место, где Вы, как показывают результаты поиска, сможете найти более 3000 логарифмических линеек. Также их можно приобрести по дешёвке в местных магазинах. Часто люди не понимают, для чего нужны логарифмические линейки, поэтому только рады избавиться от них. Кроме того, если люди узнают, что Вы коллекционер, они могут просто так подарить Вам логарифмические линейки, которые некогда принадлежали их дальним родственникам. Им будет приятно знать, что Вы их сохраните.

Если Вы решили купить логарифмическую линейку, убедитесь, что у неё работает шкала С и не запотевает прозрачный движок. Их ремонт или замена – весьма кропотливый труд. Также избегайте линеек со следами коррозии или выцветшими отметками. Их можно восстановить, но это требует немало сил и времени. В Интернете можно найти советы, как правильно чистить различные линейки.

Если Вы приобрели логарифмическую линейку, то должны помнить, что она, как и любая другая вещь, требует особого ухода. Чтобы её подвижные части хорошо работали, протирайте их полиролью для мебели (если линейка деревянная). Раньше люди смазывали железные логарифмические линейки вазелином. Важно также постоянно поддерживать логарифмическую линейку в чистоте и следить за тем, чтобы грязь не попадала под движок.

Также не следует оставлять линейку под прямыми солнечными лучами. Кроме того, старайтесь избегать использования мыла, воды и других веществ, которые могут повредить Вашу линейку.
Логарифмические линейки когда-то были своего рода компьютерами и, возможно, заменят нам современные ПК, когда придёт Апокалипсис.

Устройство

Линейка логарифмическая (стандартная) изготавливалась из плотной древесины, стойкой к истиранию. Для этого в промышленных масштабах использовалось грушевое дерево. Из него изготавливался корпус и движок – планка меньшего размера, монтируемая во внутреннем пазе. Ее можно перемещать параллельно основанию.

Бегунок изготавливался из алюминия или стали со смотровым окошком из стекла или пластика. На него нанесена тонкая вертикальная линия (визир). Бегунок двигается по боковым направляющим и подпружинивается стальной пластинкой. Корпус и движок облицованы светлым целлулоидом, на котором тиснением нанесены шкалы. Их деления заполнены типографской краской.

Разновидности

Стандартная линейка логарифмическая имеет длину измерительной шкалы 25 см. Выпускался еще карманный вариант длиной 12,5 см и устройство повышенной точности 50 см. Существовало деление линеек на первый и второй сорта в зависимости от качества исполнения. Внимание уделялось четкости наносимых штрихов, обозначений и вспомогательных линий. Движок и корпус должны были быть ровными и идеально подогнаны друг к другу. Изделия второго сорта могли иметь незначительные царапины и точки на целлулоиде, но они не искажали обозначений. Также мог присутствовать незначительный люфт в пазах и прогиб.

Существовали и другие карманные (похожие на часы диаметром 5 см) варианты устройства – логарифмическая дисковая (типа «Спутник») и круговая (КЛ-1) линейки. Они отличались и конструкцией, и меньшей точностью измерений. В первом случае для установки чисел на замкнутых круговых логарифмических шкалах использовалась прозрачная крышка с линией-визиром. Во втором – механизм управления (две вращающиеся ручки) был смонтирован на корпусе: одной управлялся дисковый движок, другая управляла стрелкой-визиром.

Логарифмическая линейка

Логарифмическая линейка — аналоговое вычислительное устройство, позволяющее выполнять несколько математических операций, в том числе умножение и деление чисел, возведение в степень (чаще всего в квадрат и куб), вычисление квадратных и кубических корней, вычисление логарифмов, потенцирование, вычисление тригонометрических и гиперболических функций и некоторые другие операции. Если разбить вычисление на три действия, то с помощью логарифмической линейки можно возводить числа в любую действительную степень и извлекать корень любой действительной степени.

Стандартная линейка имела длину 30 см, что было удобно для геометрических работ с форматом А4. При этом логарифмические шкалы имели длину 25 см, на концах обычно наносились их обозначения. Реже встречались линейки малого размера со шкалами длиной 12,5 см и большого размера — со шкалами длиной 50 см. Выпускались также круговые логарифмические линейки (логарифмические круги), преимущество которых заключалось в их компактности. До появления карманных калькуляторов этот инструмент служил незаменимым расчётным орудием инженера.

Построение правильного шестиугольника

Типы линеек

В течение длительного времени линейки изготавливались из различных материалов и в различных размерах. Линейки обычно производят из пластика или дерева, реже из металлов. Пластмассы также использовались с момента их изобретения; их можно отливать в форму с помощью маркировки длины, а не писать.

Металл используется для более долговечных линеек для использования в мастерской; иногда металлическая кромка встроена и в деревянную настольную линейку, чтобы сохранить её при использовании для прямолинейной резки. 30-см линейка полезна в черчении. Более короткие линейки удобны для хранения в малых пространствах. В некоторых случаях необходимы более длинные линейки, например, 46 см.

Используются также жесткие деревянные или пластиковые палочки длиной 1 ярд и измерительные палочки длиной 1 метр в качестве однозначной меры длины. Классически для крупных проектов использовались длинные измерительные стержни, замененные рулеткой, колесным землемером или лазерными дальномерами.

Линейка для черчения букв

Настольные линейки используются для трех основных целей: для измерения, для помощи в черчении прямых линий и в качестве прямой направляющей для резки и с помощью лезвия. Практичные линейки по краям имеют метки расстояния.

Тканевая рулетка

Гибким инструментом измерения длины, который не обязательно является прямым в использовании, является тканевая рулетка. Длина рулетки калибруется в дюймах и сантиметрах. Используется для измерений вокруг твердого тела, например, для измерения талии человека, а также линейных измерений, например, внутренней стороны ноги. Когда она не используется, сворачивается, занимая мало места.

Правило сокращения предусматривает более крупные деления, чем стандартные меры, для обеспечения усадки отливок из металла. Также может называться как правило сжатия.

Для измерения пикселей на экране компьютера или мобильного телефона можно использовать программу-линейку, также называемой линейкой экрана.

Угольники

В геометрии и картографии линейка используется только для проведения прямых линий, измерение расстояния по линейке считается грубым из-за наличия погрешности от параллакса вносимой толщиной линейки. Для более точного измерения применяют измерительный циркуль, раствор которого затем прикладывают к линейке.

Линейка поперечного масштаба (ЛПМ-1) предназначена для нанесения и определения расстояний на топографических картах и планах.

Логарифмическая линейка в XXI веке

Часы Breitling Navitimer.

Логарифмические линейки широко использовались для выполнения инженерных расчётов примерно до начала 1980-х годов, когда они были вытеснены калькуляторами.

Однако в начале XXI века логарифмические линейки получили второе рождение в наручных часах: следуя моде, производители некоторых марок (среди которых Breitling, Citizen, Orient) выпустили модели со встроенной логарифмической линейкой, выполненной в виде вращающихся колец со шкалами вокруг циферблата. Производители обычно называют такие устройства «навигационная линейка».

Их достоинство — можно сразу, в отличие от микрокалькулятора, получить информацию, соответствующую табличной форме представления (например, таблицу расхода топлива на пройденное расстояние, перевода миль в километры, подсчёт пульса, определение скорости поезда и тому подобное). Однако в большинстве случаев логарифмические линейки, встроенные в часы, не оснащены шкалами для вычисления значений тригонометрических функций.

Немного фактов

В средние века монахи, которые были самым грамотным слоем населения того времени, использовали для этого тонкие свинцовые пластинки. В ряде европейских стран и в Древней Руси для работ по черчению использовали металлические прутья, которые в летописях описаны как «шильцы» или «правильца».

Все описанные приспособления были далеко не самыми удобными, и так кажется сейчас, когда в нашем распоряжении есть достаточно удобная линейка, которая может быть любой формы и длины. Но в тот момент альтернативы не было. Люди использовали то, что имели, чертили при помощи дощечек и железа, потому что сравнить было попросту не с чем.

Такое существо, как человек, устроено таким образом, что постоянно старается стремиться ко всему новому, совершенствовать то, что уже есть. Именно так постепенно усовершенствовали даже линейку. Кто может знать – возможно, через какое-то время у нас будут только умные лазерные линейки-карандаши, и будет достаточно одного взмаха, чтобы чертеж был готов.

И люди будут удивляться даже тогда: неужели было время, когда предыдущее поколение использовали стандартную деревянную/металлическую/пластмассовую линейку? Какие же они древние! Но на данный момент линейка нам нужна, и это факт.

Если копнуть не просто глубже, но еще и шире

…, то линейки бы могло и не быть, если бы не был придуман метр (мера измерения). В 1789 году во Франции, как уже было упомянуто, стали развиваться действия революции. Может показаться, а каким тут боком будет выходить линейка? Но революция стала своеобразным толчком, катализатором. Ученым поступило задание о том, что требуется ввести обновленную систему мер.

В тот момент во Франции заменяли все старое на новое, в целом, как и во всем мире. В тот момент заменяли календарь, наименование месяцев, государственное устройство, деньги, и даже систему мер это не обошло стороной. И тогда 8 мая 1790 года (в некоторых источниках указано 8 апреля) был принят Декрет о реформе мер (принимало его Учредительное Национальное Собрание).

В тот момент была собрана комиссия, в составе которой было множество ученых. Комиссия представила проект о том, чтобы принять в качестве метра одну сорокамиллионную долю от протяженности меридиана земли. Введение подобной единицы измерения в системе мер во Франции перешло со временем все границы, и это стала международная мера. Метр внедрился в каждую страну и стал международной мерой.

Но все это было после, а сначала подобную систему мер официально не захотело принимать Английское Королевское общество, наверное, не желали напрягаться. Англичане приняли решение наблюдать со стороны, и справедливо полагали, что если действительно что-то выйдет, то они примут это, и будут использовать для своих целей, а если не выйдет, то терять будет нечего, и позориться не придется. Умный ход.

Тогда в гордом одиночестве французы начали точное измерение длины меридиана земли. Такой работой руководили лучшие из лучших академиков. Замеры производили в революционное время, а это сильно усложнило процесс, и саму группу пару-тройку раз арестовывали из-за недоразумений.

Ценой огромных усилий работа была окончена, и вот, за новую единицу длины приняли точно измеренную сорокамиллионную часть географического меридиана (а его длина составляет 40 000 км), и как раз один из них проходил через Париж. Французские академики измерили его дугу на протяженности от Барселоны до Дюнкерка. Как видите, линейка – интересная вещь, если знать, какая скрывается история за ее созданием.

Источник