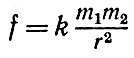охарактеризуйте основные положения методики обучения математике приведите примеры педкампус
Глава II. Основные положения преподавания математики
1. О содержании математических курсов
Как это ни странно, уже само понимание предмета математики, а значит, его содержание и расстановка в нем акцентов, вызывает разногласие. Мы будем исходить из следующего основного положения.
Положение первое. В курсе математики изучаются математические модели.
Как уже говорилось, объектами изучения в математике являются не реальные явления, а абстрактные логические объекты и структуры, у которых описан ряд отношений между их элементами (будем их коротко, как и прежде, называть математическими моделями), не размерные величины, а безразмерные. Математика изучает соотношения между элементами математических моделей, количественные и качественные связи между ними. Для математики важна не природа рассматриваемых объектов, а лишь имеющиеся между ними соотношения. Одна и та же математическая модель может описывать (с определенным приближением) свойства очень далеких друг от друга по своему конкретному содержанию реальных явлений. Так, например, формула
может описывать и закон Ньютона притяжения масс и закон Кулона притяжения электрических зарядов. Величины масс и зарядов, фигурирующие в этих законах, измеряются в разных единицах, имеют разную размерность. В математической же формуле соответствующие этим законам математические операции (в данном случае умножение и деление) производятся по правилам действия над числами, независимо от того, значениями каких физических величин они являются.
Из сформулированного положения следует, что смысл математического понятия не зависит от области его дальнейшего применения, в частности, не зависит от специализации студента, которому разъясняется это понятие.
При этом следует подчеркнуть различие смысла и содержания математического понятия как такового и конкретного явления, для описания которого оно используется, например, понятия производной векторной функции и понятия скорости механического движения, понятия интеграла и понятия работы и т. п.
Сущность математики должна находить свое отражение при обучении математике прежде всего в разъяснении истинного смысла изучаемых математических понятий.
Это утверждение, кажущееся многим бесспорным, тем не менее часто оспаривается. Некоторые считают, что те, кто интересуется математикой не самой по себе, а лишь математическими методами исследования конкретных задач, т. е. приложениями математики, должны обучаться специальной математике, а не той, которой занимаются сами математики. На самом деле такой специальной математики не существует. Смысл теоремы Пифагора или формулы конечных приращений Лагранжа не зависит от того, кто их использует: инженер или научный работник, прикладник или чистый математик. От будущей специальности студента зависну лишь содержание и объем курса математики, отбор математических понятий и фактов, отбор методов, общность и детализация изложения, подбор примеров, иллюстрирующих применение изучаемых математических понятий и методов к решению прикладных задач.
Не случайно в настоящее время наблюдается ярко выраженная упоминавшаяся выше тенденция сближения университетского и высшего технического образования на основе более общего подхода к изучаемым предметам. Современные темпы развития науки и техники таковы, что в силу быстрого изменения конкретных условий работы делается не выгодным готовить узких специалистов. Сейчас все больше потребность в специалистах, которые могут быстро ориентироваться при изменении ситуации, способны правильно оценивать происходящие изменения, приводящие иной раз к качественно совершенно новым явлениям. Эти качества прививаются не узко специальным образованием, а широким общим образованием университетского типа. Уже сейчас во многих передовых высших учебных заведениях, готовящих специалистов по современной науке и технике, математические (а также физические, химические и др.) курсы изучаются по одинаковой программе, не зависящей от будущей специальности студента (например, физической, химической, аэродинамической и т п.).
Много говорится и о том, что учить математике инженеров надо своими особыми методами, не так, как это делают математики. Этот вопрос мы рассмотрим позже, когда будем обсуждать вопросы методики преподавания.
Все сказанное здесь предполагает, безусловно, что рассматриваемые математические понятия изучаются для их дальнейшего использования при математических методах исследования тех или иных вопросов. В случае же, когда знакомятся с математическими понятиями лишь с целью использования их для описания конкретного явления, часто нет нужды разбираться в смысле используемого математического понятия, и можно ограничиться знакомством с ним на интуитивном уровне. На этом вопросе мы также остановимся подробнее ниже, когда будем обсуждать пятое положение.
Охарактеризуйте основные положения методики обучения математике приведите примеры педкампус
Задание 1
Какие информационно-коммуникационные технологии (ИКТ) Вы считаете наиболее эффективными в педагогической практике? Какие ИКТ Вы находите наименее приемлемыми в социальной педагогике? Ответ аргументируйте.
Задание 2
Раскройте основные общенаучные принципы и подходы методологии педагогики, применимые в практической работе социального педагога. Приведите примеры их реализации.
Задание 3
Опишите познавательные психические процессы, сопровождающие процесс обучения.
Задание 4
Охарактеризуйте социально-педагогические технологии работы социального педагога.
Задание 5
Изложите основные положения современной теории обучения и воспитания.
Добрый день! Помогите, пожалуйста)
Задание 1
Какие информационно-коммуникационные технологии (ИКТ) Вы считаете наиболее эффективными в педагогической практике? Какие ИКТ Вы находите наименее приемлемыми в социальной педагогике? Ответ аргументируйте.
Задание 2
Раскройте основные общенаучные принципы и подходы методологии педагогики, применимые в практической работе социального педагога. Приведите примеры их реализации.
Задание 3
Опишите познавательные психические процессы, сопровождающие процесс обучения.
Задание 4
Охарактеризуйте социально-педагогические технологии работы социального педагога.
Задание 5
Изложите основные положения современной теории обучения и воспитания.
Добрый вечер, помогите, пожалуйста.
Задание 1
Какие информационно-коммуникационные технологии (ИКТ) Вы считаете наиболее эффективными в педагогической практике? Какие ИКТ Вы находите наименее приемлемыми в социальной педагогике? Ответ аргументируйте.
Задание 2
Раскройте основные общенаучные принципы и подходы методологии педагогики, применимые в практической работе социального педагога. Приведите примеры их реализации.
Задание 3
Опишите познавательные психические процессы, сопровождающие процесс обучения.
Задание 4
Охарактеризуйте социально-педагогические технологии работы социального педагога.
Задание 5
Изложите основные положения современной теории обучения и воспитания.
Лекция. Методы обучения математике
Ищем педагогов в команду «Инфоурок»
Методы обучения математике
Цель: рассмотреть и охарактеризовать методы обучения математике
Методом обучения называют способ упорядоченной взаимосвязанной деятельности преподавателя и обучаемых, направленной на решение задач образования.
Метод обучения – это способ совместной деятельности учителя и учащихся, направленные на решение задач обучения.
Метод обучения – это способ организаций учебно-познавательной деятельности ученика с заранее определенными задачами, уровнями познавательной активности, учебными действиями и ожидаемыми результатами для достижения дидактических целей.
Прием – это элемент метода, его составная часть, разовое действие, отдельный шаг в реализации метода или модификация метода, в том случае, когда метод небольшой по объему или простой по структуре.
Одной из важных задач обучения является формирование у школьников познавательной самостоятельности, а значит, актуальными становятся методы познания, позволяющие, с одной стороны, осуществлять обучение школьников, включая их в процесс исследования, приобщая к исследовательской деятельности, с другой, вооружать их методами, необходимыми для самостоятельного познания.
Одним из наиболее универсальных математических методов познания является метод математических моделей (математическое моделирование).
Математическая модель – это описание какого-либо класса явлений реального мира на языке математики. Метод моделирования дает возможность применять математический аппарат к решению практических задач. Понятия числа, геометрической фигуры, уравнения, неравенства, являются примерами математических моделей. К методу математического моделирования в учебном процессе обращаются при решении любой задачи с практическим содержанием. Чтобы решить такую задачу математическими средствами, ее поэтапно переводят на язык математики, переходя от словесной модели к графической, а затем и к символической. Последняя модель и является математической моделью ситуации описанной в задаче. В процессе математического моделирования широко используются кодирование ситуации и декодирование построенной модели, абстракции, обобщения.
Разумеется, в конкретном опыте т и п обозначают определенные числа. Поэтому полученное равенство является лишь одной из посылок, с помощью которых уже другим методом (индукцией) получают общий закон коммутативности сложения натуральных чисел: « т + п = п + т для любых натуральных чисел т и п ».
Важно отметить, что с помощью эмпирических методов (наблюдения, опыта, измерений) выполняется лишь начальный этап работы по математическому описанию реальных ситуаций. Получаемый математический материал (интуитивные понятия, гипотезы, совокупности математических предложений) подлежит дальнейшей обработке уже другими методами
Сравнение и аналогия – логические приемы мышления, используемые как в научных исследованиях, так и в обучении в качестве метода.
С помощью сравнения выявляется сходство и различие сравниваемых предметов, т. е. наличие у них общих и различных свойств.
Например, сравнение треугольника и четырехугольника раскрывает их общие свойства: наличие сторон, вершин, углов, столько же вершин и углов, сколько сторон. Устанавливается и различие: у треугольника три вершины (стороны), у четырехугольника – четыре.
Сравнение приводит к правильному выводу, если выполняются следующие условия:
1) сравниваемые понятия однородны;
2) сравнение осуществляется по таким признакам, которые имеют существенное значение.
Рассуждение по аналогии имеет следующую общую схему:
Заключение по аналогии является лишь вероятным (правдоподобным), а не достоверным. Поэтому аналогия, как правило, не является доказательным рассуждением, т. е. рассуждением, которое может служить доказательством. Однако в обучении, как, впрочем, и в науке, аналогия часто полезна тем, что она наводит нас на догадки, т. е. служит эвристическим методом. В обучении же математике не менее важно, чем учить доказывать, это учить догадываться, что именно подлежит доказательству и как найти это доказательство.
Часто та или иная последовательность в изучении учебного материала обосновывается возможностью использования аналогии в обучении. Например, изучение вычислительных приемов в курсе математики начальных классов опирается на сходство приемов вычислений.
В практике обучения математике аналогия все еще ис-пользуется недостаточно. Иногда высказываются опасения, что с помощью аналогии мы можем прийти к ложным заключениям.
Однако не следует опасаться возникновения ложных заключений по аналогии. Необходимо лишь считать их гипотезами (предположениями). Ошибки, допускаемые в процессе поиска, исследования, вполне правомерны, так как чаще всего поиск ведется способом «проб и ошибок». Нередко учитель не дает учащимся, отвечающим на вопросы учителя, ошибаться. В этом отражается тот факт, что учебная деятельность учащихся в этом случае является лишь репродуктивной деятельностью, а в такой деятельности ошибки недопустимы. Воспроизводить следует безошибочно. В продуктивной же, творческой деятельности ошибки неизбежны. Такого рода ошибками являются и те, которые появляются в результате применения аналогии в процессе поиска. Они являются составной частью метода проб и ошибок. Важно, чтобы учащиеся в поиске правильных ответов сами могли находить ошибочность возникающих в этом процессе предположений. Этому, разумеется, надо их учить.
Обобщение и абстрагирование – два логических приема, применяемые почти всегда совместно в процессе познания.
Обобщение – это мысленное выделение, фиксирование каких-либо общих существенных свойств, принадлежащих только данному классу предметов или отношений.
Абстрагирование – это мысленное отвлечение, отделение общих, существенных свойств, выделенных в результате обобщения, от прочих несущественных или различных свойств рассматриваемых предметов или отношений и отбрасывание (в рамках нашего изучения) последних.
Когда мы говорим «несущественные свойства», то имеем в виду несущественные с математической точки зрения. Один и тот же предмет может изучаться, например, физикой или математикой. Для физики существенны одни его свойства, для математики другие. Математика изучает лишь форму, размеры, расположение предмета.
Из приведенного краткого разъяснения вытекает, что абстрагирование не может осуществляться без обобщения, без выделения того общего, существенного, что подлежит абстрагированию.
Обобщение и абстрагирование неизменно применяются в процессе формирования понятий, при переходе от представлений к понятиям.
Под обобщением понимают переход от единичного к общему, от менее общего к более общему, а под конкретизацией понимают обратный переход – от более общего к менее общему, от общего к единичному.
Если обобщение используется при формировании понятий, то конкретизация используется при описании конкретных ситуаций с помощью сформированных ранее понятий.
Рассмотрим переход от единичного к общему, Например, формирование понятия «квадрат» на раннем этапе обучения начинается с показа множества предметов, отличающихся друг от друга формой, размерами, цветом, материалом, из которого они сделаны. Дети, после того как им показывают на одну из этих фигур и говорят, что это квадрат, безошибочно отбирают из множества фигур все те, которые имеют такую же форму, пренебрегая различиями, в размерах, цвете, материале. Здесь выделение из множества предметов подмножества производится по одному еще недостаточно проанализированному признаку – по форме. Дети еще не знают свойств квадрата, они распознают его только по форме. Такое распознавание встречается у детей 4-5 лет. Дальнейшая работа по формированию понятия квадрат состоит в анализе этой формы с целью выявления ее свойств. Учащимся предлагается путем наблюдения найти, что есть общего у всех отобранных фигур, имеющих форму квадрата, чем они отличаются от остальных. Устанавливается, что у всех квадратов 4 вершины и 4 стороны. Но у некоторых фигур, которые мы не отнесли к квадратам, тоже 4 вершины и 4 стороны. Оказывается, у квадрата все стороны равны и все углы прямые.
В развивающих системах обучения широко используется метод проблемного изложения.
Метод проблемного изложения состоит из следующих приемов:
1) создание проблемной ситуации;
2) постановка проблемы (учебной задачи);
3) поиск решения проблемы (ход решения и его логика, возможные и действительные затруднения и противоречия);
4) математическая запись решения проблемы ;
5) обобщение нового знания;
6) обобщение способа деятельности.
Эвристическая беседа или частично-поисковый метод.
Метод получил название частично-поискового потому, что учащиеся не всегда могут самостоятельно решить сложную учебную проблему от начала и до конца. Заключается в организации активного поиска решения выдвинутых в обучении (или самостоятельно сформулированных) познавательных задач под руководством педагога, поскольку не всегда еще могут самостоятельно решить сложную проблему. Знания же учащиеся добывают самостоятельно, отвечая на поставленные вопросы учителя или разрешая проблемные задания. Роль учителя: не сообщение или изложение знаний, а организация поиска новых знаний при помощи разнообразных средств. Учащиеся решают проблемные ситуации, анализируют, сравнивают, обобщают, приходят к познанию нового. Процесс мышления приобретает продуктивный характер, но при этом поэтапно направляется и контролируется педагогом или самими учащимися. Эвристическая беседа состоит из следующих методических приемов:
1) создание проблемной ситуации;
2) формулирование проблемы учителем или учащимися;
3) организация поиска решения проблемы : учитель задает вопросы и дает задания поискового характера, учащиеся отвечают, выполняют задания;
4) математическая запись учащимися решения проблемы;
5) формулировка учащимися выводов;
6) обобщение учащимися знаний и способов действия.
Приведем пример использования данного метода на этапе введения новых знаний при изучении раздела «Устные вычисления». Поскольку дети еще только учатся способам познавательной деятельности, их внимание следует обратить на использование возможных вспомогательных учебных средств (раздаточного материала, рисунков, схем и т. д.). Трудность состоит в том, чтобы найти, как использовать этот материал для решения проблемы, для подтверждения своего предположения.
Этот метод, в отличие от предыдущих методов, предполагает полную самостоятельную творческую деятельность учащихся. Даже при его простых вариантах он предполагает готовность ученика к целостному самостоятельному решению проблемы, к поиску и приобретению новых знаний, новых способов деятельности. Этот метод имеет следующие функции:
1) он является основным методом обучения опыту творческой деятельности и формирования черт творческой деятельности;
2) организует творческое усвоение знаний, т.е. учит применять уже известные знания для решения проблемных задач и добывать новые в результате такого решения;
3) обеспечивает овладение методами научного познания;
4) является условием формирования интереса, потребности в творческой исследовательской деятельности.
Постановка учебной задачи принадлежит учащимся. Роль учителя сводится к оперативному управлению процессом решения поставленной проблемы. После анализа материала, постановки проблем и задач и краткого устного или письменного инструктажа обучаемые самостоятельно изучают литературу, средства для достижения результата, ведут наблюдения, измерения, выполняют другие действия поискового характера. Инициатива, самостоятельность, творческий поиск, проявляются в исследовательской деятельности наиболее полно. Методы учебной работы непосредственно перерастают в методы научного исследования. Данный метод можно использовать только после того, как ранее уже были использованы методы проблемного изложения материала и частично-поисковый (эвристическая беседа). Исследовательский метод состоит из приемов:
1) создание проблемной ситуации;
2) формулирование проблемы (учебной задачи);
3) поиск решения проблемы, выдвижение гипотез;
4) доказательство или опровержение гипотезы;
5) символическая запись выводов и их формулирование;
Проблемная ситуация, способы еѐ создания
Создание проблемной ситуации есть предпосылка и форма предъявления учащимся учебной задачи. Учебная деятельность содержит в себе планомерное и последовательное создание учителем проблемных ситуаций и включение учащихся в решение этих проблемных ситуаций. «Явления, обозначаемые понятием «проблемная ситуация», включает три главных компонента: а) необходимость выполнения такого действия, при котором возникает познавательная потребность в новом, неизвестном отношении, способе или условии действия; б) неизвестное, которое должно быть открыто в возникшей проблемной ситуации; в) возможности учащегося в выполнении поставленного задания, в анализе условий и открытии неизвестно. Ни слишком трудное, ни слишком легкое задание не вызовут проблемной ситуации». Проблемная ситуация возникает тогда, когда ученик наталкивается на некоторое противоречие, на что-то непонятное, неизвестное. Проблемная ситуация – средство организации проблемного обучения, это «препятствие», «интеллектуальная трудность», вызывающая познавательную потребность учения и создающая внутренние условия для активного усвоения новых знаний и способов деятельности.
М.И. Махмутов выделяет четыре типа проблемных ситуаций:
1) если учащиеся не знают способа решения поставленной задачи, у них недостаточно знаний для объяснения нового факта;
2) когда ученики сталкиваются с необходимостью использовать ранее усвоенные знания в новых практических условиях;
3) если имеется противоречие между теоретически возможным путем и практической осуществимостью данного способа;
4) когда учащиеся сталкиваются с противоречием между практически достигнутым результатом и его теоретическим обоснованием.
Учитель создает проблемную ситуацию, направляет учащихся на ее решение, организует поиск решения. Таким образом, ребенок становится в позицию исследователя, и, как результат, у него образуются новые знания, он овладевает новыми способами действия. Трудность управления проблемным обучением состоит в том, что возникновение проблемной ситуации – акт индивидуальный, поэтому от учителя требуется использование дифференцированного и индивидуального подхода. Проблемную ситуацию создает не всякий вопрос, задача или противоречие. Если на тот или иной вопрос или задачу у ученика имеется готовый ответ, здесь не требуется по существу никаких мыслительных усилий, кроме припоминания и воспроизведения уже известных знаний. Познавательная же проблема характеризуется тем, что выводит ученика за пределы имеющихся у него знаний. При этом в ней есть что-то неизвестное, требующее поиска, мыслительной деятельности. В зависимости от содержания учебного материала, возрастных особенностей учащихся выделяют различные способы создания проблемной ситуации:
1. Способ аналогий. В этом случае мы опираемся на имеющийся у учащихся житейский опыт или же актуализируем ранее полученные знания для решения новых задач. Например, по какому правилу подобраны выражения в каждом столбике? Составь по тому же правилу выражения 3-го столбика
2. Индуктивный, аналитико-синтетический способ. Учащиеся самостоятельно исследуют явления и факты и делают необходимые научные выводы. Например, догадайся! По какому правилу записаны выражения в каждом столбике? Вычисли их значения. Дополни записи третьего столбика.
3. Выдвижение проблемного вопроса. Этот прием используется тогда, когда для решения проблемы и овладения новыми знаниями нужно творчески применить какой-то ранее изученный принцип или закономерность. Например, при изучении табличных случаев умножения 9 возможно задание такого вида. Можешь ли, не вычисляя значений выражений ответить на вопрос: «Какие равенства верные, а какие неверные?»
4. Сообщение парадоксального факта, выдвижение гипотез, предположений. Учитель: Все суммы делятся на 4.
5. Сообщение противоположных точек зрения на один и тот же факт. Методы проблемного обучения могут сопровождаться подчеркиванием противоречивых положений, заключенных в содержании учебного материала, и их объяснении учащимися. Например, как можно рассуждать, вычисляя значение произведений: 37·2; 38·2; 39·2? Различные виды рассуждений:
1) 37·2=37+37=74, тогда 38·2=76, 39·2=78
2) 37·2=(30+7)·2=30·2+7·2=60+14=74, тогда 38·2=(30+8)·2=30·2+8·2=60+16=76
3) 37·2=37+37=74, значит 2·37=74; 38·2=2·38=74+2=76, 39·2=78
Какой поиск решения наиболее рациональный?
Способы создания проблемных ситуаций. Назовем некоторые из них:
1. Проблемная ситуация возникает, когда учитель преднамеренно сталкивает жизненные представления учащихся с фактами, для объяснения у школьников не хватает знаний, жизненного опыта.
2. В школьной практике широкое применение получили проблемные ситуации, возникающие при несоответствии известного и требуемого способа действия. Учащиеся сталкиваются с противоречиями, когда их побуждают выполнять новые задачи старыми способами.
3. Проблемные ситуации можно создать, побуждая учащихся к сравнению, сопоставлению фактов, явлений.
4. Для активизации мыслительной деятельности учащихся исключительное значение имеют проблемные ситуации, созданные в результате столкновения мнений самих учащихся.
Таким образом, при использовании проблемных ситуаций, создается осознанное затруднение учащегося, преодоление которого требует творческого поиска, заставляет ученика мыслить, искать выход, рассуждать, переживать радость от правильно найденного решения, что способствует возникновению интереса к изучаемому, эффективности процесса обучения математики.
1. Цели и задачи обучения, уровень обучения, который необходимо достигнуть.
2. Содержание и методы определенной науки вообще и предмета, темы в частности.
3. Количество и сложность учебного материала.
4. Учебные возможности школьников (возрастные особенности, уровень подготовленности, сформированность учебных навыков, учебная тренированность и выносливость, особенности классного коллектива).
5. Возможности учителя (опыт, уровень подготовленности, знание типичных ситуаций процесса обучения).
6. Применение методов на предыдущих уроках.
7. Тип и структура занятия и др.
Кратко рассмотрим использование методов на каждом этапе изучения темы.
Подготовительная работа обеспечивает необходимые условия для успешного усвоения материала всеми учащимися класса. На этой ступени можно использовать как метод беседы, так и метод самостоятельной работы с последующим обобщением.
При ознакомлении с новым материалом типа сведений (правила порядка выполнения арифметических действий в выражениях, ознакомление с терминами, с некоторыми приемами вычислений), во время инструктажа учеников по использованию инструментов (линейки, циркуля и т.п.) и в других подобных случаях используется метод объяснения .
Изложение материала должно быть четким, доступным, непродолжительным по времени. При этом по мере необходимости используются наглядные пособия – наглядный метод.
При ознакомлении учащихся с математическими понятиями (число, арифметическое действие и др.), с теоретическими знаниями типа закономерностей (свойства арифметических действий, связи между компонентами и результатами действий и т.п.) чаще всего используется метод беседы. Система упражнений в этом случае должна вести детей от частных фактов к общему выводу, к «открытию» той или иной закономерности, т. е. здесь целесообразна эвристическая беседа, обеспечивающая индуктивный путь рассуждения.
При ознакомлении с новым материалом индуктивным путем учитель, проводя беседу, предлагает учащимся ряд упражнений. Учащиеся выполняют их, затем, анализируя, выделяют существенные стороны формируемого знания, в результате чего делают соответствующий вывод, т.е. приходят к обобщению.
К системе упражнений предъявляется ряд требований.
1. Система упражнений должна обеспечивать наглядную основу формируемого знания.
2. Упражнения надо подбирать так, чтобы, анализируя их, учащиеся смогли бы выделить все существенные стороны формируемого знания. Для этого подбираются упражнения так, чтобы сохранялись существенные стороны, а несущественные изменялись.
В начальном обучении наиболее эффективен индуктивно-дедуктивный метод, когда от рассмотрения частных случаев (задач, выражений) осуществляется переход к общим выводам и правилам, а затем на основании общих положений осмысливаются другие частные факты. Например, индуктивным путем формируется понятие о виде задачи: ученики решают ряд задач данного вида, выделяя в них существенное, типичное. Затем, встречая задачу, ученик при анализе ее содержания находит в ней те существенные признаки, которые характерны для задач этого вида, относит ее к данному виду и находит правильный способ ее решения.
В начальных классах иногда при ознакомлении с новым материалом используется метод самостоятельных работ: учащиеся самостоятельно выполняют упражнения и приходят к выводу, т.е. в приобретении знаний они используют исследовательский (проблемный) метод.
При закреплении полученных знаний широко используется метод самостоятельных работ. При этом полезно предлагать упражнения дифференцированно, учитывая возможности каждого из детей.
В начальном курсе математики также используется лабораторный (практический) метод. Данный метод преимущественно используется при ознакомлении учеников с величинами: длиной, массой, емкостью, временем, площадью, объемом и др., с их свойствами и способами измерения.
1. Дайте определение понятия «метод», «прием».
2. Назовите методы, применяемые при обучении математике.
3. Дайте характеристику проблемной ситуации.
4. Что необходимо учитывать при выборе методов обучения?