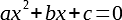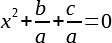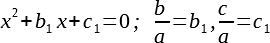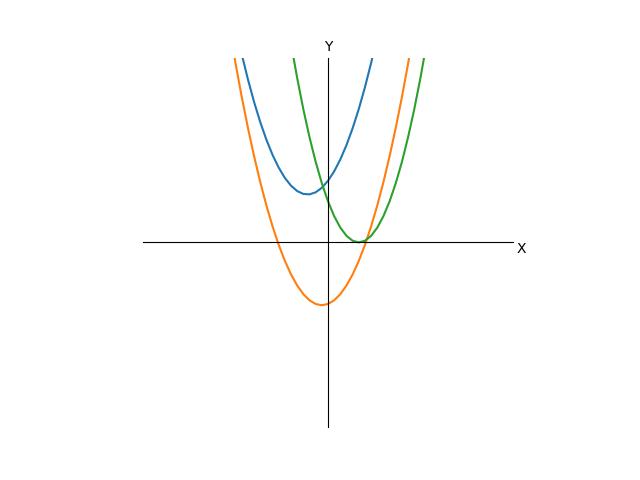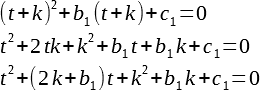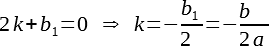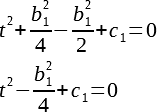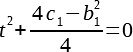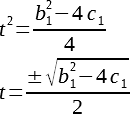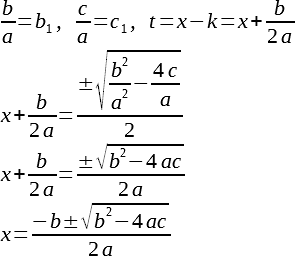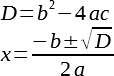зачем нужны квадратные уравнения
квадратные уравнения. зачем?
какие практические задачи обыватель может свести к квадратному уравнению?
Это смотря, что за обыватель.
Все задачи обывателя решит специализированное ПО в его мозговом импланте айфоне.
Обывателю не обязательно быть знакомым ни с азами биологии, ни с азами химии, ни с азами физики, ни с азами астрономии, ни с азами географии, геологии, истории, экономики, права, etc.
Нужно только уметь читать короткие фразы и тыкать грязным пальцем в иконки.
Но вот если ты хочешь воспитать не обывателя-потреблядину, а человека-творца, то квадратные уравнения станут ценной крупинкой в его картине мироздания.
Например задачи, в которых возникает теорема Пифагора
рассчёт траектории кинутого камня, например
эээ извелечение корня это всё таки очень частный случай.
или есть задача(практическая) с теоремой Пифагора в которой
сложные проценты, амортизация оборудования, катание с горки, стрельба навесом, прыжок с окна 🙂 примеры см в школьных учебниках физики и математики;
то что люди с психикой испорченной математикой сводят к дифурам, простые люди сводят по возможности к более понятным степенным уравнениям, причём даже не заморачиваются их формальным написанием..или забивают болт 🙂
рассчёт траектории кинутого камня, например
Не смеши. Когда ты на практике швыряешь камни, меньше всего ты думаешь об уравнениях. Тем более ты не думаешь о них, когда играешь в энгри бёрдз.
Квадратные уравнения для гуманитариев и школьников.
Ну вот, наконец настало время запилить первый свой познавательный пост.
Все в школе решали квадратные уравнения, там вам рассказывали про дискриминант, что два корня, и все такое, причем, скорее всего, в подробности не вдаваясь. Мне в какой-то момент стало интересно, а почему все так, а не иначе, откуда взялись эти дискриминанты, почему корней два, а не три или сколько-то еще. Вообще, я люблю представлять себя математиком древности, который открывает что-нибудь. Типа, вот раньше чего-то не было, а он взял и вывел. Как это могло происходить?
Конечно, я буду использовать современные достижения математики, которые, возможно, не были известны первооткрывателям тех же квадратных уравнений, но строгости это не уменьшает, поэтому такой подход меня устраивает.
Итак, что же такое квадратное уравнение? Это уравнение вида:
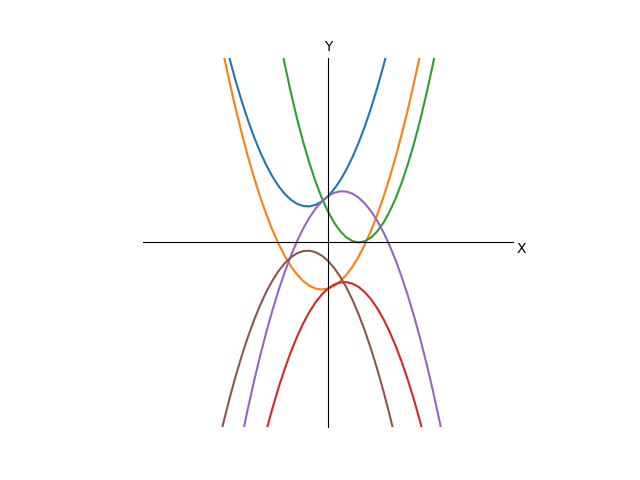
У нас тут общий случай, то-есть неизвестны конкретные значения констант, поэтому честно нарисовать график квадратичной функции сразу мы не можем. Сперва я хотел исследовать функцию всеми доступными методами(дабы аргументированно рисовать график), но потом решил, что, раз для нахождения решения нам нам хватит чисто арифметических действий, лучше не усложнять и не лезть в производные. Поэтому я решил нарисовать несколько графиков, неподходящие из которых мы будем отсеивать по мере продвижения к решению.
Итак, допустим, наша функция будет представлять собой один из графиков, пока мы не знаем, какой.
Теперь, попробуем как-нибудь изменить исходную функцию, чтобы она стала проще, но сохранила свойства исходной. У нас три константы, а это многовато, давайте попробуем избавиться от как можно большего их количества. Для начала, мы можем поделить все уравнение на a. а заведомо не равна нулю, так как если бы была равна, наше уравнение превратилось бы в простое линейное, которое, будем считать, уже всем известно, как решать. Тогда у нас получится новое уравнение:
Чтобы не тащить возможное нагромождение дробей, мы назовем для краткости константы новыми именами, а уравнение преобразуется к виду:
А что там с графиком стало от такого преобразования? По сути, на правую часть уравнения это никак не повлияло, а функция слева сжалась(или растянулась, в зависимости от того, больше модуль а, чем единица, или меньше) пропорционально коэффициенту a к осиX, а если а было отрицательным, то еще и перевернулась вверх ногами. Самое важное здесь для нас то, что пересечение графиков с осью X вообще никак не изменилось, значит, искомое решение уравнения осталось тем же самым. Кроме того, теперь мы можем быть точно уверены, что у новой функции «рога» направлены вверх, ведь х в квадрате теперь с положительным коэффициентом, а значит, при больших по модулю значениях х, как не трудно догадаться, этот член будет положительным и будет расти быстрее, чем оставшиеся два члена.
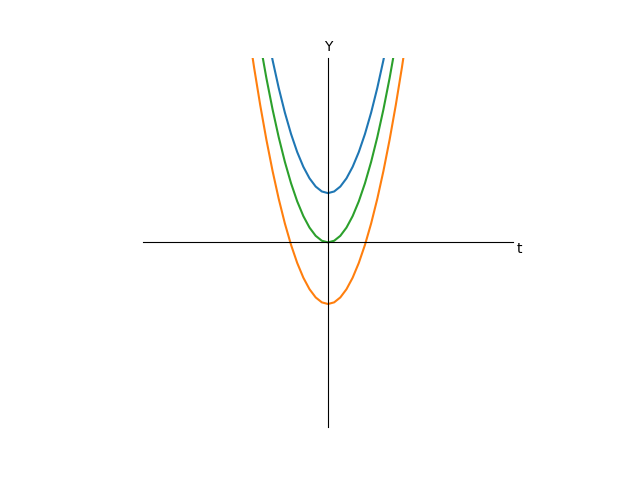
Теперь наши графики буду выглядеть как-то так, мы убрали из них все те, что рогами вниз:
Все внимание на коэффициент перед t в первой степени. Благодаря тому, что мы можем k выбрать произвольно, мы можем сделать так, чтобы этот коэффициент стал равным нулю, а значит, t в первой степени исчезнет из уравнения, и оно еще упростится!
Подставим найденное k в предыдущее выражение, упростим, получим:
Как видно, переменная t осталась только в виде квадрата без коэффициентов, все остальное ушло в одну константу. Но что вообще это преобразование делает с графиком? Оно просто-напросто сдвигает график влево на расстояние k(если k положительное, и в вправо в противном случае). Стало быть, если у нас было пересечение с нулем, то оно и останется, но сдвинется в какую-то сторону, а если не было, то его и не появится. Можно заметить, что если мы поменяем t на -t, то ничего не изменится(квадрат аннигилирует минус), значит, функция стала четной, отражение графика функции от оси Y ничего не меняет, следовательно, преобразование, которое мы сделали, превращает график в симметричный относительно оси Y, причем все линии одинаковые, за исключением того, что находятся на разной высоте.
Рассмотрим повнимательнее последнее выражение, его можно переписать в виде:
Очевидно, что так как t в квадрате может быть только неотрицательным, то минимум функции достигается при t=0. Следовательно, если второе слагаемое(а можно считать, что только его числитель) положительно, то функция до нуля не достанет и решений уравнения, стало быть, нет. Это случай синей кривой на графике. Если нам так повезло, что что слагаемое равно нулю, то очевидным единственным решением будет 0, это зеленая кривая. Если же слагаемое отрицательно, то существуют какие-то решения, это оранжевая кривая. Это три случая, имеют принципиальную разницу, все остальное многообразие возможных уравнений сводится к этим трем. Теперь разберемся, сколько же там корней. Выразим t из последнего выражения(будем считать, что обратную функцию для квадрата мы знаем):
Но мы нашли какое-то t, а нам ведь надо найти х. Для этого, выполним все преобразования, которые мы сделали над уравнением, теперь уже над его решением в обратном порядке, а именно просто подставим все то, что мы назаменяли:
Ой, а что это у нас тут под корнем такое знакомое. Да это же дискриминант!
Ну вот, собственно, и все, решение получено. Хотел еще про правила Виета написать, но, думаю не стоит, пост и так большой, а правила эти весьма просты.
Исследовательская работа «Квадратные уравнения»
Ищем педагогов в команду «Инфоурок»
Муниципальное бюджетное общеобразовательное учреждение
«Сергачская средняя общеобразовательная школа №3»
Квадратные уравнения: от истоков к современности
Выполнила ученица 8 «а» класса
Никулина Анастасия, 14 лет
Руководитель: Маслова Елена Владимировна
3. Способы решения квадратных уравнений …………………………… ….10-15
С квадратными уравнениями мы знакомы из школьного курса алгебры. В учебнике алгебры 8 класса под редакцией С.А.Теляковского нам представляют квадратные уравнения, как уравнения второй степени. Предлагаются некоторые способы решения квадратных уравнений, а также решение задач с помощью квадратных уравнений. Но к сожалению, о применении уравнений на практике в учебнике ничего не сказано.
На уроке нам учитель сообщила, что есть и другие способы решения квадратных уравнений и можно для каждого вида уравнений выбрать эффективный способ. Я решила самостоятельно изучить способы решения квадратных уравнений, которых нет в учебнике, а также выяснить имеют ли применение в жизни квадратные уравнения.
Цель работы: Расширить свои знания о квадратных уравнениях
Познакомиться с историей появления и развития квадратных уравнений
Используя дополнительную литературу, изучить способы решения, которых нет в учебнике
Узнать применение квадратных уравнений в жизни
Объект исследования : квадратные уравнения
Предмет: исследования квадратных уравнений
Актуальность темы: Теория уравнений занимает ведущее место в алгебре и математике в целом. Сила теории уравнений в том, что не только имеет теоретическое значение для познания естественных законов, но и служит практическим целям. Большинство жизненных задач сводится к решению различных видов уравнений, и чаще это уравнения квадратного вида.
Гипотеза: Предполагаю, что квадратные уравнения можно решить многими способами, и они находят своё применение в жизни человека
Есть ли иные способы решения квадратных уравнений отличные от тех, что предложены в учебнике и зачем нам в жизни нужны квадратные уравнения
1 . Странички истории
Квадратные уравнения в Древнем Вавилоне
Много лет назад возникла необходимость решать уравнения второй степени. Потребность обусловлена нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей эры вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.
При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные. Вот, к примеру, одна из его задач.
Задача «Найти два числа, зная, что их сумма равна 20, а произведение – 96».
или же 100 – х 2 =96, х 2 =4
Ясно, что, выбирая в качестве неизвестного полу разность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения.
Квадратные уравнения в Индии
Задачи на квадратные уравнения встречаются уже в астрономическом трактате «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:
В уравнении (1) коэффициенты, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.
В Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму. Вот одна из задач знаменитого индийского математика XII в. Бхаскары. «Стая обезьян забавляется: восьмая часть всего числа их в квадрате резвится в лесу, остальные двенадцать кричат на вершине холмика. Скажите мне, сколько всех обезьян?»
После извлечения квадратного корня получаем: x – 32 =16.
Квадратные уравнения в Европе XII-XVII в.
Формы решения квадратных уравнений по образцу Аль-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202г. итальянским математиком Леонардом Фибоначчи. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел.
Эта книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из этой книги переходили почти во все европейские учебники XIV-XVII вв. Общее правило решения квадратных уравнений, приведенных к единому каноническому виду х 2 + bx = c при всевозможных комбинациях знаков и коэффициентов b, c, было сформулировано в Европе в 1544 г. М. Штифелем.
Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.
Истоки алгебраических методов решения практических задач связаны с наукой древнего мира. Как известно из истории математики, значительная часть задач математического характера, решаемых египетскими, шумерскими, вавилонскими писцами-вычислителями (XX—VI вв. до н. э.), имела расчетный характер. Однако уже тогда время от времени возникали задачи, в которых искомое значение величины задавалось некоторыми косвенными условиями, требующими, с нашей современной точки зрения, составления уравнения или системы уравнений. Первоначально для решения таких задач применялись арифметические методы. В дальнейшем начали формироваться начатки алгебраических представлений. Например, вавилонские вычислители умели решать задачи, сводящиеся с точки зрения современной классификации к уравнениям второй степени. Был создан метод решения текстовых задач, послуживший в дальнейшем основой для выделения алгебраического компонента и его независимого изучения.
Это изучение осуществлялось уже в другую эпоху сначала арабскими математиками (VI—Х вв. н. э.), выделившими характерные действия, посредством которых уравнения приводились к стандартному виду приведение подобных членов, перенос членов из одной части уравнения в другую с переменой знака. А затем европейскими математиками Возрождения, в итоге длительного поиска создавшими язык современной алгебры, использование букв, введение символов арифметических операций, скобок и т. д. На рубеже XVI—XVII вв. алгебра как специфическая часть математики, обладающая своим предметом, методом, областями приложения, была уже сформирована. Дальнейшее ее развитие, вплоть до нашего времени, состояло в совершенствовании методов, расширении области приложений, уточнении понятий и связей их с понятиями других разделов математики.
Аль – Хорезми — арабский учёный, который в 825 г. написал книгу «Книга о восстановлении и противопоставлении». Это был первый в мире учебник алгебры. Он также дал шесть видов квадратных уравнений и для каждого из шести уравнений в словесной форме сформулировал особое правило его решения.
В трактате Хорезми насчитывает 6 видов уравнений, выражая их следующим образом:
1. «Квадраты равны корням», т.е. ах 2 = вх.
2. «Квадраты равны числу», т.е. ах 2 = с.
3. «Корни равны числу», т.е. ах = с.
4. «Квадраты и числа равны корням», т.е. ах 2 + с = вх.
5. «Квадраты и корни равны числу», т.е. ах 2 + вх = с.
Разберём задачу аль – Хорезми, которая сводится к решению квадратного уравнения. «Квадрат и число равны корням.» Например, один квадрат и число 21 равны 10 корням того же квадрата, т.е. спрашивается, из чего образуется квадрат, который после прибавления к нему 21 делается равным 10 корням того же квадрата?» х 2 + 21 = 10х
Франсуа Виет — французский математик, сформулировал и доказал теорему о сумме и произведении корней приведённого квадратного уравнения.
Искусство, которое я излагаю, ново или по крайней мере было настолько испорчено временем искажено влиянием варваров, что я счел нужным придать ему совершенно новый вид . Франсуа Виет
Виет Франсуа (1540-13.12. 1603) родился в городе Фонтене ле-Конт провинции Пуату, недалеко от знаменитой крепости Ла-Ро-шель. Он был широко образованным человеком. Знал астрономию и математику и все свободное время отдавал этим наукам.Главной страстью Виета была математика. Он глубоко изучил сочинения классиков Архимеда и Диофанта, ближайших предшественников Кардано, Бомбелли, Стевина и других. Виета они не только восхищали, в них он видел большой изъян, заключающийся в трудности понимания из-за словесной символики: Почти все действия и знаки записывались словами, не было намека на те удобные, почти автоматические правила, которыми мы сейчас пользуемся. Нельзя было записывать и, следовательно, начать в общем виде алгебраические сравнения или какие-нибудь другие алгебраические выражения. Каждый вид уравнения с числовыми коэффициентами решался по особому правилу. Поэтому необходимо было доказать, что существуют такие общие действия над всеми числами, которые от этих самих чисел не зависят. Виет и его последователи установи, что не имеет значения, будет ли рассматриваемое число количеством предметов или длиной отрезка. Главное, что с этими числами можно производить алгебраические действия и в результате снова получать числа того же рода. Значит, их можно обозначать какими-либо отвлеченными знаками. Виет это и сделал. Он не только ввел свое буквенное исчисление, но сделал принципиально новое открытий, поставив перед собой цель изучать не числа, а действия над ними. Такой способ записи позволил Виету сделать важные открытия при изучении общих свойств алгебраических уравнений. Не случайно за это Виета называют «отцом» алгебры, основоположником буквенной символики.
2. Способы решения квадратных уравнений
1. СПОСОБ : Разложение левой части уравнения на множители
2. СПОСОБ : Метод выделения полного квадрата
3. СПОСОБ : Решение квадратных уравнений по формуле
4. СПОСОБ : Графическое решение квадратного уравнения
5. СПОСОБ : Решение уравнений с использованием теоремы Виета
Все вышеперечисленные способы подробно разобраны в учебнике, поэтому на них я не буду останавливаться. Разберём ещё несколько способов.
6. СПОСОБ : Решение уравнений способом «переброски»
Рассмотрим квадратное уравнение ах 2 + bх + с = 0, где а ≠ 0.
Умножая обе его части на а, получаем уравнение а 2 х 2 + аbх + ас = 0.
Решим уравнение 2х 2 — 11х + 15 = 0.
Решение. « Перебросим» коэффициент 2 к свободному члену и сделав замену получим уравнение у 2 — 11у + 30 = 0.
Согласно обратной теореме Виета
7. СПОСОБ: Свойства коэффициентов квадратного уравнения
Пусть дано квадратное уравнение ах 2 + bх + с = 0, а ≠ 0
1. Если a+ b + с = 0 ( т.е. сумма коэффициентов уравнения равна нулю), то х 1 = 1, х 2 = c/а
Решим уравнение 132х2 + 247х + 115 = 0
8. СПОСОБ: Решение квадратных уравнений с помощью циркуля и линейки
При этом возможны три случая
1) Радиус окружности больше ординаты центра, окружность пересекает ось Ох в двух точках
2) Радиус окружности равен ординате центра, окружность касается оси Ох в точке
3) Радиус окружности меньше ординаты центра, окружность не имеет общих точек с осью абсцисс, в этом случае уравнение не имеет решения.
Проведем окружность радиуса S A, где А (0;1)
9. СПОСОБ : Геометрический способ решения квадратных уравнений
В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведем ставший знаменитым пример из «Алгебры» ал-Хорезми.
Решим уравнение х 2 + 10х = 39.
В оригинале эта задача формулируется следующим образом: «Квадрат и десять корней равны 39».
Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD, достраивая в углах четыре равных квадрата, сторона каждого их них 2,5, а площадь 6,25.
х 2 + 10х числом 39, получим, что S = 39 + 25 = 64, откуда следует, что сторона квадрата ABCD, т.е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим
Преобразуя уравнение, получаем
10. СПОСОБ: Решение уравнений с использованием теоремы Безу
Теорема Безу и её следствие рассматриваются в старших классах. Смысл состоит в том, что нужно подставить в уравнение вместо неизвестной все целые делители свободного члена уравнения, и поделить столбиком наш трехчлен на (х- а), где а – найденный корень. Затем разложить на множители и найти остальные корни. Приведу пример:
Разделим р (х) на (х-1)
3. Жизнь по «параболе»
Школьном курсе алгебры мы знакомимся с квадратными уравнениями и уравнениями, сводящимися к квадратным. Однако они применяются не только для решения более сложных уравнений. Мы встретим квадратные уравнения в экономических дисциплинах, в различных программах для обработки звука и видео, а также в векторной графике.
Многие обучающиеся даже не догадываются, что график квадратичной функции, парабола, встречается в разных областях нашей жизни. Приведу несколько примеров.
При разбеге прыгуна для максимально четкого попадания на планку отталкивания и высокого полета используют расчеты, связанные с параболой. Подобные расчеты нужны и при метании снаряда. Дальность полета объекта зависит от квадратного уравнения. Даже беговая дорожка стадиона, параболической формы, для плавного прохождения дистанции.
Мы с удовольствием наблюдаем красивейшее оптическое явление – радуга. Еще ученые древности задавались вопросом формы радуги. Она полукруглая. Форма радуги определяется формой капель воды, в которых преломляется солнечный свет. А форма капли- круглая.
Даже струя воды, выбрасываемая из фонтана принимает форму параболы.
Дельфины – прекрасные создания. Они сопровождают суда и начинают выпрыгивать из воды, демонстрируя при этом движение по параболе.
Человечество прошло длинный путь от незнания к знанию, непрерывно заменяя на этом пути неполное и несовершенное знание все более полным и совершенным.
В ходе выполнения своей исследовательской работы я считаю, что с поставленной целью и задачами я справилась, мне удалось узнать о квадратных уравнениях гораздо больше, чем в школьном курсе алгебры. Мне было интересно узнать о различных способах решения квадратных уравнений, а также узнать где же они применяются. Способов решения квадратных уравнений очень много. Я изучила 10 способов решения квадратных уравнений. Надо отметить, что не все они удобны для решения, но каждый из них уникален. Некоторые способы решения помогают сэкономить время, что немаловажно при решении заданий на ГИА.
Подводя итоги, можно сделать вывод, что гипотеза моя подтвердилась. Квадратные уравнения играют огромную роль в математике. Эти знания могут пригодиться нам на протяжении всей жизни, и я думаю, что мою презентацию можно использовать в учебном процессе, чтобы заинтересовать увлекающихся математикой школьников и просто тех детей, которые не видят смысла в квадратных уравнениях
6.Пресман А.А. Решение квадратного уравнения с помощью циркуля и линейки.М., Квант, №4/72. С.34.
7.Дидактические материалы по алгебре. М., Математика (приложение к газете «Первое сентября»), №№ 21/96, 10/97.
8.Баранова Е.А. Как увлечь школьников исследовательской деятельностью. Математика в школе / Е.А. Баранова, М.И.Зайкин// 2004. №2 – 80с.
9.Глейзер Г.И. История математики в школе. 7-8 классы. – М.: Просвещение, 1982.
10.Дробышев Ю.А. Изучение квадратных уравнений на основе историко – генетического метода /Ю.А. Дробышев // /. Математика в школе № 6 –2011.
11.С.А. Литвинова, и др. За страницами учебника математики 8-11 классы. – 2-е изд., дополненное – М.: Глобус, Волгоград: Панорама,2008.– c.76-82.
12.Макарычев Ю. Н. Алгебра: учебник для 8 класса общеобразовательных учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под редакцией С. А. Теляковского. – 11-е издание – М.: Просвещение, 2003. – 238 с.