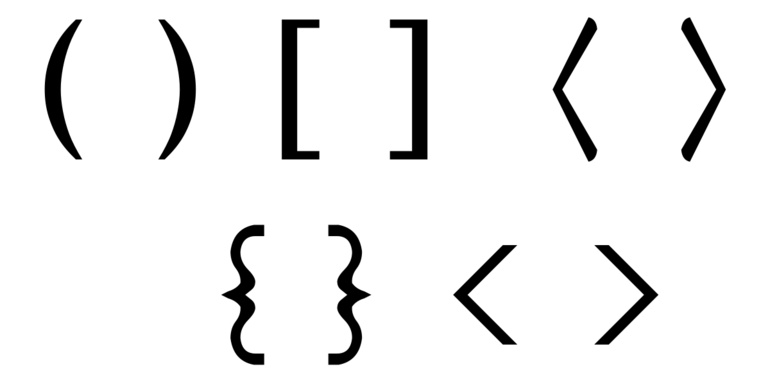зачем нужны фигурные скобки
Как и когда ставить текст в скобках. Правила русского языка
Скобки – парный знак препинания, который выполняет выделительную функцию. Различают круглые, квадратные, фигурные и угловые скобки. Копирайтеры в своей работе чаще всего ставят круглые скобки. Рассмотрим более подробно варианты использования скобок в тексте.
Вставные конструкции со скобками
Круглые скобки необходимы, если в предложении содержатся вставные конструкции. Такие конструкции могут находиться только в середине или в конце предложения и обычно заключаются в скобки. Этот знак препинания является рекомендованным, может заменяться запятыми или тире.
Скобки ставят, если надо уточнить значение отдельных слов, дать попутное указание, разъясняющее смысл фразы, или вставить замечание, дополняющее высказывание. Приведем примеры основных значений вставных конструкций:
Конкретизация в маркированных списках, прайс-листах: Штукатурка (выравнивание стен). Монтаж пластикового уголка (наружного, внутреннего).
Пояснение отдельных слов: Рекомендации по профилактике эмоционального выгорания предоставил Иванов И.И. (доктор медицинских наук, член-корреспондент РАН).
Пояснение основного содержания: Ключевая задача рекламы товара – максимально отличаться от конкурента (выступать как опознавательный знак) и быть узнаваемой потребителями.
Дополнение смысла высказывания: Нужна постоянная практика и знание правил копирайтинга (часть их Вы уже изучили).
Выражение эмоций автора текста: Каждый человек обязан (я подчеркиваю – обязан!) заботиться о своем физическом и психическом здоровье.
Скобки при оформлении цитат
Если требуется после цитаты указать источник цитирования или фамилию автора, то эта информация заключается в скобки. Приведем примеры.
Верховный суд указал, что «цитирование производится для иллюстрации, подтверждения или опровержения высказывания автора» (Определение ВС РФ № 78-ГОЗ-77 от 05.12.2003).
«Клиент получает ту рекламу, которую он заслуживает!» (Огилви Д. Откровения рекламного агента). Заглавие источника отделяется точкой от фамилии автора и не заключается в кавычки.
Сочетание скобок и других знаков
Важно помнить, что перед скобкой (открывающей или закрывающей) никогда не ставится знак препинания: запятая, двоеточие, точка с запятой, тире. Эти пунктуационные знаки уместны после закрывающей скобки.
Возьмите на заметку! Не используйте предложения с двойными скобками. Если внутри одной вставной конструкции надо вставить еще одну, то внешнее (первое вводное предложение) выделяется скобками, а внутреннее – при помощи тире.
Скобки редко встречаются в тексте и поэтому привлекают внимание читателей. Всегда помните, что и как ставить в скобки.
<> (Фигурные скобки)
Фигурные скобки <> (также называются просто «скобки») – важный элемент языка программирования С. Они используются в нескольких различных конструкциях, приведенных ниже, и это может иногда сбивать с толку начинающих.
Открывающая скобка «<» должна всегда сопровождаться закрывающей скобкой «>«. Это условие, известное как парность (симметричность) фигурных скобок. Arduino IDE (интегрированная среда разработчика) включает подходящий инструмент для проверки парности скобок. Достаточно выделить скобку, или даже поставить курсор сразу же за скобкой, как будет подсвечена её логическая пара.
Сейчас эта возможность работает с ошибкой, так как IDE часто ищет (некорректно) скобку в тексте, который «закомментирован».
Начинающие программисты или программисты, перешедшие на Си с Бейсика, часто считают использование фигурных скобок сбивающим с толку или пугающим. В конце концов, одни и те же фигурные скобки заменяют оператор RETURN в подпрограммах (функциях), оператор ENDIF в условных циклах и оператор NEXT в циклах FOR.
Поскольку использование фигурных скобок столь многогранно, хорошей практикой программирования будет печатать закрывающую фигурную скобку сразу после того, как напечатана открывающая скобка, когда вставляется конструкция, для которой нужно использовать фигурные скобки. Затем возвращаем курсор в позицию между фигурными скобками и начинаем вводить операторы. Ваши скобки всегда будут парными и не лишат вас душевного равновесия.
Непарные скобки могут часто приводить к скрытым, непонятным ошибкам компиляции, которые сложно отследить в большой программе. Из-за их разного использования, скобки также невероятно важны в синтаксической правильности программы и перемещение скобки на одну или две строки часто приводят к значительному воздействию на логику программы.
Скобки в математике
Вы будете перенаправлены на Автор24
Скобки в математике играют очень важную роль: с помощью них задаётся порядок действий с выражением, обозначаются границы промежутков и необходимость выполнения какого-либо действия над выражением. Также с помощью скобок обозначаются вектора и матрицы и действия с множествами.
Использование круглых скобок в математике
Круглые скобки в математике встречаются наиболее часто, и они используются для множества целей.
Первое применение.
С помощью круглых скобок устанавливается порядок действий для вычисления алгебраического выражения. Выражение, которое стоит в скобках, вычисляется первым, за ним следует вычисление всех остальных.
В случае же если в выражении скобок много и одна находится внутри другой — первыми вычисляются скобки с максимальной глубиной вложенности.
Второе применение.
Третье применение.
Круглые скобки также используются для обозначения действий, которые необходимо совершить над всем выражением, стоящим в скобках. Под действием здесь имеются в виду возведение в степень, взятие производной или вычисление подинтегрального выражения.
$(x+2)^2; \int_1^5 (x^2+5x)dx; f’(x)= (5x^2 + 1)’$
Четвёртое применение.
Пятое применение.
Готовые работы на аналогичную тему
Пятое применение.
Квадратные скобки в математике
Что же означают квадратные скобки в математике и для чего они используются?
Квадратные скобки в математике встречаются реже чем круглые, но всё же их можно встретить довольно часто.
Первое применение.
Квадратные скобки иногда используются при записи выражений наряду с круглыми для того, чтобы было проще различить скобки и, соответственно, задаваемый ими порядок действий. Часто с такой целью квадратные скобки используются для записи формул физики и других технических наук.
Второе применение.
Третье применение.
С помощью квадратной скобки записывают совокупности. Совокупности — это системы уравнений, для которых справедливы все множества решений для каждого уравнения, входящего в совокупность.
$\left [ \begin
Фигурная скобка в математике
Первое применение.
С помощью символа фигурной скобки обозначают систему уравнений, решением которой являются корни, подходящие для всех уравнений, включённых в систему.
Второе применение.
Третье применение.
Треугольные скобки
Общая характеристика
Главная задача знаков — описание этапов осуществляемых действий. Математическое уравнение или выражение имеет одиночную пару квадратных, фигурных и других скобок, а также может использовать их некоторое количество.
Значение и разновидности
Скобки — это парные знаки, используемые во всевозможных областях. Чтобы правильно выстроить фразу в русском языке, для понимания смысла текста в предложении они употребляются как знаки препинания. С начальных классов школы изучают основы этих знаков.
В расчетах первая из скобок считается открывающей, а вторая — замыкающей. Оба знака соответствуют друг другу, но также используются те, в которых открытие или закрытие не различается (косые /…/, прямые скобки |…|, двойные прямые ||…||. Раскрывать значение можно чаще всего в математике, физике, химии и остальных науках для указания важности выполнения операции в формулах. На компьютерной клавиатуре представлены все виды знаков препинания.
Разновидности:
Открытие круглых () произошло в 1556 году для подкоренного выражения. По правилу первым выполняется действие внутри знака, затем произведение или определение частного (деление), а в конце — суммирование и разница.
В Microsoft word, Excel включена электронная конфигурация этих знаков. Часто используемые виды скобок, следующие: (), [ ], < >(), [ ], < >. Также встречаются двойные, называемые обратными (]] и [ [) или > в виде уголка. Их использование является двойственным — с открывающейся и замыкающей скобочкой.
Основные цели квадратной скобки в математике:
Другие варианты расчета:
Квадратные скобки в математике обозначают, что действие выполняется последовательно. Эти знаки позволяют разграничить операции.
Треугольные актуальны в теории групп. Правило записи ⟨ a ⟩ n характеризует циклическую группу порядка n, сформированную элементом a.
Круглые (операторные) () используются в математике для описания первостепенности действий. Например, (1 +5)*3 означает, что нужно сначала сложить 1 и 5, а затем полученную величину перемножить на 3. Наряду с квадратными, используются для записи разных компонент векторов, матриц и коэффициентов.
На уроке математики преподаватель объясняет, как раскрыть скобки в уравнении для последующего решения. Фигурная одинарная < встречается при решении систем уравнений, обозначает пересечение данных, а [[ используется при их слиянии.
Одинарные или двойные выражения
Употребление [] происходит реже. Одно уравнение со скобками объединяет несколько значений или неравенств различных размеров. Для решения совокупности нужно выполнить любое условие. Конец, завершение действия замыкает закрывающий знак.
В персональных компьютерах, ноутбуках, нетбуках встроена кодировка Юникод, закрепленная не за левыми или правыми объединяющими знаками, а за открывающими и замыкающими, поэтому при воспроизведении печатного текста со скобочками в режиме «справа налево» каждый знак меняет внешнее направление на обратное.
Квадратные скобки в уравнении означают, что установлен порядок действий, задаются границы промежутков и необходимость выполнения действия над выражением. Двойные квадратные скобки необходимы для записи выражений наряду с круглыми для рационального порядка действий.
По правилам интервал [−a;+a] записывается в виде нестрогого неравенства −a≤x≤a, означающего, что x находится на промежутке от −a до a включительно.
В середине парного знака с отделяющей точкой или запятой указываются два числа — наименьшее, затем большее, ограничивающие интервал. Круглая скобочка, прилегающая к цифре, означает невключение числа в промежуток, а квадратная — добавление.
В некоторых учебных пособиях для вузов встречаются расшифровки числовых интервалов, в которых вместо круглой скобочки (применяется обратная квадратная скобка ], и наоборот. В обозначениях запись ]0, 1[ равносильна (0, 1).
Открытая квадратная скобка (символ [) значит, что совокупность представляет систему уравнений разных размеров, для которых справедливы все множества решений для каждого уравнения, входящего в общее задание. Например, [x+11=2yy2−12=0
Прежде чем решать задачу или выполнять задание, нужно правильно определить принципы действий. В некоторых случаях скобочки могут быть не нужны, а иногда их обязательно нужно поставить.
Прочие знаки
Для математических, алгебраических и прочих расчетов важно знать различие обобщающих знаков. От правильности вычислений зависит итоговый результат.
Удобство записи системы уравнений
Применение фигурных знаков относится к представлению совмещения множеств. При решении системы с фигурной скобкой уравнения пересекаются, а [] объединяет их.
фигурные скобки
Смотреть что такое «фигурные скобки» в других словарях:
фигурные скобки — Скобки в виде «<>«. [http://www.morepc.ru/dict/] Тематики информационные технологии в целом EN braces … Справочник технического переводчика
Скобки — У этого термина существуют и другие значения, см. Скобки (значения). Сюда перенаправляются запросы 🙂 и некоторые другие, начинающиеся с двоеточия. О них см. статью смайлик. ( ) Название символа Скобки Юникод U+0028 29 HTML … Википедия
скобки — (Square brackets, Parantheses, Angle brackets, Braces) Парные знаки препинания. Бывают квадратные, круглые, угловые (ломаные), фигурные (парантезы). Применяются в формульном наборе и для выделений в тексте … Шрифтовая терминология
скобки — парный знак препинания для выделения отдельных слов или частей предложения, содержащих пояснения к основному тексту. В математике употребляются для обозначения порядка выполнения математических действий. Различают скобки круглые ( ),… … Энциклопедический словарь
Скобки — парный выделительный знак препинания, имеющий различное начертание: (), [], <>, <>, //. С. употребляются для выделения слов, словосочетаний и предложений, содержащих добавочные замечания и пояснения к осн. части текста. Квадратные, ломаные… … Российский гуманитарный энциклопедический словарь
Угловые скобки — Сюда перенаправляются запросы 🙂 и некоторые другие, начинающиеся с двоеточия. О них см. статью смайлик. Скобки парные знаки, используемые в различных областях. Различают: круглые () скобки; квадратные [ ] скобки; фигурные < >скобки; угловые… … Википедия
brace — Фигурные скобки (Brace) Парные знаки препинания [точка, запятая, двоеточие, тире, многоточие и т.д.]. Скобки, имеющие сложную изогнутую форму. Фигурные скобки чаще всего употребляются в математических формулах, где они обычно объединяют… … Шрифтовая терминология
Математические обозначения — Список используемых в математике специфических символов можно увидеть в статье Таблица математических символов Математические обозначения («язык математики») сложная графическая система обозначений, служащая для изложения абстрактных… … Википедия
фигурный — прил., употр. сравн. часто конструкции, вещи 1. Фигурной конструкцией называют такую конструкцию, предмет и т. п., которые имеют сложные очертание, форму, украшены множеством декоративных деталей. Фигурный мост. | Фигурная мебель. | Фигурный… … Толковый словарь Дмитриева
Си (язык программирования) — У этого термина существуют и другие значения, см. Си. Запрос «Язык программирования Си» перенаправляется сюда; см. также другие значения. Си Класс языка: процедурный Тип исполнения: компилируемый Появился в: 1969 1973 Автор( … Википедия