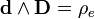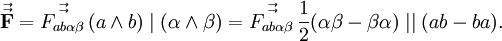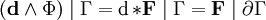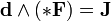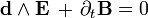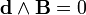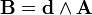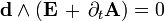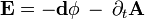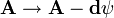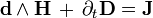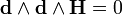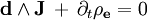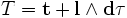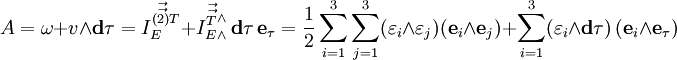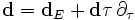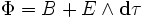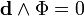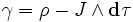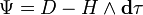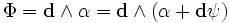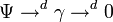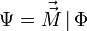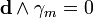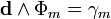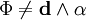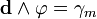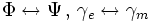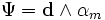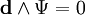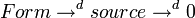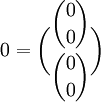зачем нужны дифференциальные формы

Классическая механика: о диффурах «на пальцах»

Введение

В этой статье я продолжаю тему цифровой обработки сигналов. В ней я постараюсь простым языком рассказать о концепции игровой механики (физики) с использованием подхода на основе дифференциальных уравнений. В будущем я собираюсь оценить действительно ли реализация такого подхода приведет к резкому увеличению вычислительной нагрузки. В рамках этой статьи не получится — слишком большой объем. В этой я собираюсь описать назначение коэффициентов, входящих в математическую модель динамического объекта, описать их физический смысл, т.е. их влияние на поведение динамического объекта.
Начнем пожалуй…

Физический смысл

Динамика в картинках

Чтобы наглядно показать влияние коэффициентов дифф. уравнения на поведение динамического объекта решил построить графики переходного процесса при ступенчатом (step response) и импульсном (impulse response) входных воздействиях. Всего представлено 6 групп графиков (по одной группе для каждого коэффициента). Графики построены в пакете Octave (v. 3.4) с установленным пакетом «Signal Processing».
Итак, в качестве исходной возьмем модель вида:
=========================================
>>> w = tf([1 1],[1 1 1])

Transfer function «w» from input «u1» to output…

Continuous-time model.
=========================================


Код «w = tf([1 1],[1 1 1])» в символьном виде имеет вид:
>>> w = tf([b0 b1],[a0 a1 a2])
На скриншотах внизу-справа — примерное время стабилизации (коридором стабильности считаем ± 5% от заданной величины).

Попробуем поиграться с коэффициентом жесткости a2.
>>> w1 = 0.1*tf([1 1],[1 1 0.1])
y1: (s + 1)/(s^2 + s + 0.1)

>>> w2 = 10*tf([1 1],[1 1 10])
y1: (s + 1)/(s^2 + s + 10)
Примечание: пришлось подшаманить с коэффициентами усиления, чтобы результирующий коэффициент усиления был равен единице.


Что видно на графиках? Слева-направо представлены графики для w, w1 и w2, соответственно. Графики w1 более плавные и медленнее достигают установившегося значения. Графики w2 имеют более колебательный характер, но быстрее достигают установившегося значения. Вывод: жестче пружина — больше колебаний, но короче переходный процесс.

Попробуем поиграться с демпфированием (а1).
>>> w1 = tf([1 1],[1 0.25 1])
y1: (s + 1)/(s^2 + 0.25s + 1)

>>> w2 = tf([1 1],[1 2 1])
y1: (s + 1)/(s^2 + 2s + 1)


Сразу вывод: больше вязкость — быстрее затухают колебания.

Попробуем поиграться с инерцией (а0).
>>> w1 = tf([1 1],[0.1 1 1])
y1: (s + 1)/(0.1s^2 + s + 1)

>>> w2 = tf([1 1],[2 1 1])
y1: (s + 1)/(2s^2 + s + 1)


Вывод: меньше масса чугуняки — меньше болтанки и короче переходный процесс.

Перейдем к правой части и поиграемся с b1.
>>> w1 = 10*tf([1 0.1],[1 1 1])
y1: (10 s + 1)/(s^2 + s + 1)

>>> w2 = 0.25*tf([1 4],[1 1 1])
y1: (0.25 s + 1)/(s^2 + s + 1)


Вроде бы разница еле заметна, если смотреть на графики Step Response. Но на графиках Impulse Response хорошо виден эффект этого коэффициента. Если он равен единице, то график импульсного переходного процесса начинается с единицы (на самом деле он выходит из нуля, но не суть важно — второе значение в графике еденица). График w1 «начинается» со значения 10 (обратная величина от 0.1), а график w2 — начинается со значения 0.25 (обратное к 4). Таким образом, коэффициент b1 можно «обозвать» коэффициентом эффективности управления (входного воздействия).

И напоследок вкусненькое — игры с коэффициентом b0. Это хитрый коэффициент, потому и сравнение будет не таким как было выше. Чтобы показать его эффект придется варьровать несколько коэффициентов.
>>> w1 = tf([6 1],[1 1 1])
y1: (6 s + 1)/(s^2 + s + 1)

>>> w2 = tf([6 1],[1 3 1])
y1: (6 s + 1)/(s^2 + 3 s + 1)


Чем отличаются друг от друга w1 и w2? У w2 в три раза больше коэффициент демпфирования. В результате получаем интересные выводы. Графики w1 и w2 раньше пересекают уровень установившегося значения чем дефолтный график. Однако график w1 сохраняет форму дефолтного с его колебательностью, а график w2 за счет увеличенного демпфирования более сглаженный. Таким образом, играясь с форсированием и демпфированием мы можем заставить даже чугунный утюг порхать по рингу как бабочка без колебаний туда-сюда.

На правах PS

В данной статье я рассматривал лишь положительные значения коэффициентов. Их положительность — необходимое условие устойчивости мат. модели. Однако можно попробовать поиграться и с отрицательными значениями. Неустойчивой системой также можно управлять. Вспомните о самолетах пятого поколения (например, наш Беркут). Обратная стреловидность крыла — это неустойчивый планер, но зато высокая маневренность. Автоматика способна скорректировать эту неустойчивость и при этом, когда нужно, закладывать крутые виражи.
Если получится, состряпаю игрушку, с которой можно будет наглядно увидеть все эти эффекты.

Источник

СОДЕРЖАНИЕ

Примеры

Примеры в малых размерах

которые представляют реальный интерес. Формула для внешней производной d здесь имеет вид

Теорема градиента утверждает, что 1-форма точна тогда и только тогда, когда линейный интеграл формы зависит только от концов кривой, или, что то же самое, если интеграл вокруг любой гладкой замкнутой кривой равен нулю.

Аналогии с векторным полем

Концепции консервативных и несжимаемых векторных полей обобщаются до n измерений, потому что градиент и дивергенция обобщаются до n измерений; curl определяется только в трех измерениях, поэтому концепция безвихревого векторного поля не обобщается.

Лемма Пуанкаре

ведет к идентичности

Пример : в двух измерениях лемма Пуанкаре может быть доказана непосредственно для замкнутых 1-форм и 2-форм следующим образом.

Формулировка как когомологии

Используя сжимающие гомотопии, подобные тем, которые использовались при доказательстве леммы Пуанкаре, можно показать, что когомологии де Рама гомотопически инвариантны.

Применение в электродинамике

Таким образом, векторный потенциал соответствует однообразной форме потенциала А → <\ displaystyle <\ vec >>

> 0>

(Здесь постоянная магнитная проницаемость вакуума.) μ 0 <\ displaystyle \ mu _ <0>>

Источник

СОДЕРЖАНИЕ

История

Концепция

Интеграция и ориентация

которая является отрицательной величиной интеграла той же дифференциальной формы на том же интервале, когда используется противоположная ориентация. То есть:

Это придает геометрический контекст соглашениям об одномерных интегралах, согласно которым знак меняется при изменении ориентации интервала на противоположную. Стандартное объяснение этого в теории интегрирования одной переменной состоит в том, что, когда пределы интегрирования находятся в противоположном порядке ( b ), приращение dx отрицательно в направлении интегрирования.

Мультииндексная нотация

Внешняя производная

Дифференциальное исчисление

Первой идеей, ведущей к дифференциальным формам, является наблюдение, что ∂ _v f ( p ) является линейной функцией от v :

Смысл этого выражения дается путем вычисления обеих сторон в произвольной точке p : в правой части сумма определяется « поточечно », так что

поэтому найти такое f будет невозможно, если только

где ∧ определяется так, что:

Внутренние определения

По универсальному свойству внешних степеней это эквивалентно чередующемуся полилинейному отображению :

Внешняя алгебра может быть вложена в тензорную алгебру с помощью отображения чередования. Карта чередования определяется как отображение

Операции

Помимо сложения и умножения с помощью скалярных операций, которые возникают из структуры векторного пространства, существует несколько других стандартных операций, определенных для дифференциальных форм. Наиболее важными операциями являются внешнее произведение двух дифференциальных форм, внешняя производная одной дифференциальной формы, внутреннее произведение дифференциальной формы и векторного поля, производная Ли дифференциальной формы относительно векторного поля и ковариантная производная дифференциальной формы по векторному полю на многообразии с заданной связностью.

Внешний продукт

Антисимметрия, присущая внешней алгебре, означает, что когда α ∧ β рассматривается как полилинейный функционал, он является альтернированным. Однако, когда внешняя алгебра вложила подпространство тензорной алгебры с помощью отображения альтернирования, тензорное произведение α ⊗ β не является альтернированным. Существует явная формула, описывающая внешний вид продукта в этой ситуации. Внешний вид продукта

Риманово многообразие

Структуры векторных полей

Внешний дифференциальный комплекс

Откат

Интеграция

Интеграция в евклидовом пространстве

Интеграция по цепочкам

Предположим, что φ определяется формулой

Тогда интеграл в координатах можно записать как

Интеграция с использованием разделов единства

Интеграция по волокнам

Обозначим эту форму через

Затем ( Dieudonne 1972 ) доказывает обобщенную формулу Фубини ошибка harv: цель отсутствует: CITEREFDieudonne1972 ( справка )

определяется предметом интерьера

Теорема Стокса

Эта теорема также лежит в основе двойственности между когомологиями де Рама и гомологиями цепей.

Связь с мерами

Течения

Приложения в физике

Используя упомянутые выше определения, уравнения Максвелла могут быть очень компактно записаны в геометрических единицах как

Приложения в геометрической теории меры

Источник

Дифференциальные формы в электродинамике

Дифференциальные формы в электромагнетизме

Содержание

Граф Десшампа

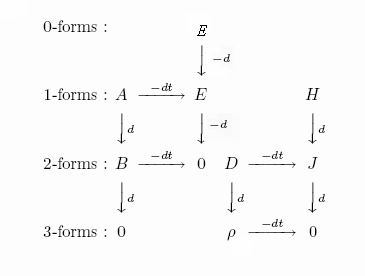
Уравнения Максвелла-Фарадея и Максвелла-Ампера с использованием дифференциальных форм в трёх измерениях, следуя Десшампу, можно изобразить в виде графа

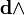
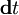
где обозначает внешнее дифференцирование формы по метрическому пространству, а — дифференцирование формы по времени. Знак минус обозначает, что дифференциал суммируется с обратным знаком.

Например, уравнения Максвелла — Ампера (сформулированные впервые Хевисайдом) можно получить из правого графа Десшампа, если записать выражения для J и D.

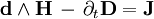
Для получения выражений, надо просуммировать (с учётом знака) все входящие стрелки (то-есть, соответствующие им дифференциалы) выбранной физической величины.

Дифференциальные формы в электродинамике

Максвелловская электродинамика весьма изящно формулируется на языке дифференциальных форм. Рассмотрим 2-форму Фарадея, соответствующую тензору электромагнитного поля:

Эта форма является формой кривизны тривиального главного расслоения со структурной группой U(1), аналогичная ситуация — лишь с другой группой — возникает в любой калибровочной теории. 3-форма тока имеет вид

или, что тоже самое (это выражение является обобщением теоремы Гаусса и теоремы Стокса):

В этих обозначениях уравнения Максвелла в геометрических единицах могут быть очень компактно записаны как

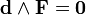
где * — оператор Ходжа (он же звёздочка Ходжа или просто звёздочка). Подобным образом может быть описана геометрическая структура любой калибровочной теории.

2-форма 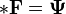также называется 2-формой Максвелла.

Обобщённый граф уравнений Максвелла для дифференциальных форм в трёхмерном пространстве

Запишем уравнения Максвелла в терминах дифференциальных форм для трёхмерного пространства. В дополнительной горизонтальной графе 2 показаны номера дифференциальных форм для трёхмерного пространства. Первая половина системы уравнений Максвелла называется уравнения Максвелла-Фарадея. При записи уравнений с использованием дифференциальных форм векторный оператор набла заменяется на операцию внешнего произведения по пространству. Для 1-формы E, которая представлена векторной физической величиной, эта операция есть . Для 2-формы В та же самая операция является . Получается уравнение для 2-формы:

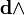
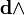
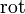
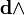
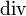
Все физические величины записаны в единицах системы СИ. Из теорема де Рама|теоремы де Рама следует: 2-форма В локально может быть представлена через 1-форму A:

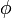
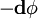
Используя снова теорему де Рама, мы определяем скалярный потенциал электрического поля 0-форму . Приравниваем выражение в скобках в последней формуле и напряжённость электрического поля, следовательно есть:

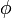
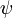
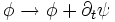
Представление полей в терминах векторного магнитного потенциала и скалярного электрического потенциала неоднозначно, так как потенциалы A и могут отличаться на любую скалярную функцию .

,

Такое условие называется условием Лоренца. Эти уравнения не зависят от природы электромагнитной среды.

Вторая половина так называемых уравнений Максвелла (впрочем сформулированных в таком виде Хевисайдом) называется уравнения Максвелла-Ампера. Вектор H заменяем на 1-форму H. Вектор D на 2-форму D. Тогда в нотации дифференциальных форм:

В правых частях этих выражений находятся плотности. J 2-форма плотности электрического тока или плотность магнитного потенциала. 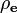3-форма плотность заряда или плотность кванта электрического поля. Применим операцию внешнего произведения по пространственной физической величине к уравнению для 2-формы. Тогда с учётом

Все выражения которые приведены выше можно представить в виде графа Десшампа (который приведён выше).

Обобщённый граф уравнений Максвелла для дифференциальных форм в четырёхмерном пространстве-времени

Запишем 1-форму для четырёхмерного времени-пространства.

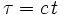
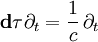
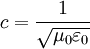
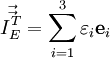
Запишем дифференциальный оператор Минковского для четырёхмерного пространства (пространство-время).

.

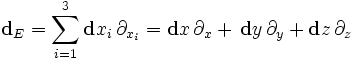
Тогда уравнения Максвелла-Фарадея сведутся в одно выражение:

Запишем 3-форму источников для уравненений Максвелла-Ампера

Запишем 1-форму 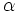для четырёхмерного потенциала электромагнитного поля (используем теорему де Рама, лемму Пуанкаре).

где 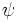0-форма или скалярная функция.

Приведём граф Десшампа для четырёхмерного пространства-времени.

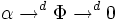
Запишем материальное уравнение для среды.

где 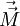— двухэлементный тензор(diadics).

Магнитные источники

Магнитный источник состоит из четырёхмерной 2-формы магнитного тока J_m и четырёхмерной 3-формы плотности магнитного заряда ρ_m :

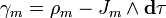
По теореме де Рама магнитный четыре ток можно представить через вторую форму:

При постоянных магнитных источниках не может быть выражена через 1-форму для четырёхмерного потенциала электромагнитного поля (используем теорему де Рама, лемму Пуанкаре):

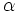
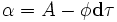
В случае электрических и магнитных источников имеем:

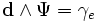
Или что тоже самое:

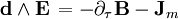
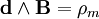
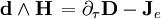
Четыре 2-Формы и Четыре источники (3-формы) взаимно заменяемы (можно трансформировать одно в другое):

При исчезающих электрических источниках ( γ_e = 0 ) Ψ может быть выажена через магнитный четыре потенциал:

Выражения для суперформ

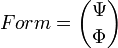
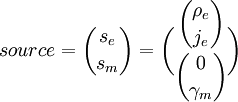
История

В статье 1981 года Десшамп [2] помещает два графа (DAG) для электромагнитных дифференциальных форм и описание аппарата дифференциальных форм. Оба графа взаимосвязи дифференциальных форм Дешампа полностью содержится в Системе Физических Величин Плотникова Н. А. Теоремы Стокса и Гаусса, а так же операции с дифференциальными формами различного порядка так же описаны в публикации Плотникова Н. А. от 1978 года.

В 2004 году Ismo V. Lindell [3] публикует книгу с подробным описанием аппарата дифференциальных форм и его применения к теории электромагнитного поля. Эта работа — отличное и глубокое введение в современный язык теории электромагнитного поля. Книга Ismo V. Lindell содержит последние результаты автора по исследованию сред со сложными электромагнитными свойствами. Ismo V. Lindell значительно развил аппарат математического описания физических процессов электромагнитного поля.

Примечания

Литература

См. также

Полезное

Смотреть что такое «Дифференциальные формы в электродинамике» в других словарях:

Дифференциальная форма — порядка или форма кососимметрическое тензорное поле типа на касательном расслоении многообразия. Дифференциальные формы были введены Эли Картаном в начале XX века. Формализм дифференциальных форм оказывается удобен во многих разделах… … Википедия

Внешний дифференциал — Дифференциальная форма порядка k или k форма кососимметрическое тензорное поле типа на касательном расслоении многообразия. Дифференциальные формы были введены Картаном в начале XX века. Формализм дифференциальных форм оказывается удобен во… … Википедия

Внешняя производная — Дифференциальная форма порядка k или k форма кососимметрическое тензорное поле типа на касательном расслоении многообразия. Дифференциальные формы были введены Картаном в начале XX века. Формализм дифференциальных форм оказывается удобен во… … Википедия

Внутренняя производная — Дифференциальная форма порядка k или k форма кососимметрическое тензорное поле типа на касательном расслоении многообразия. Дифференциальные формы были введены Картаном в начале XX века. Формализм дифференциальных форм оказывается удобен во… … Википедия

Замкнутая форма — Дифференциальная форма порядка k или k форма кососимметрическое тензорное поле типа на касательном расслоении многообразия. Дифференциальные формы были введены Картаном в начале XX века. Формализм дифференциальных форм оказывается удобен во… … Википедия

Ковектор — Дифференциальная форма порядка k или k форма кососимметрическое тензорное поле типа на касательном расслоении многообразия. Дифференциальные формы были введены Картаном в начале XX века. Формализм дифференциальных форм оказывается удобен во… … Википедия

Уравнения Максвелла — Классическая электродинамика … Википедия

Вариационные принципы — Принципами механики называются исходные положения, отражающие столь общие закономерности механических явлений, что из них как следствия можно получить все уравнения, определяющие движение механической системы (или условия её равновесия). В ходе… … Википедия

Вариационные принципы механики — Принципами механики называются исходные положения, отражающие столь общие закономерности механических явлений, что из них как следствия можно получить все уравнения, определяющие движение механической системы (или условия её равновесия).… … Большая советская энциклопедия

ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ — Принципами механики наз. исходные положения, отражающие столь общие закономерности механич. явлений, что из этих положений как следствия можно получить ур ния, определяющие движения механич. системы (или условия её равновесия). В механике… … Физическая энциклопедия

Источник