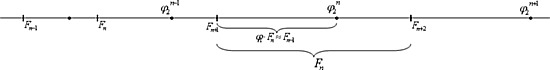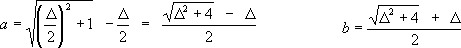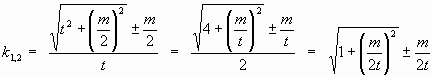зачем нужно среднее геометрическое

Среднее геометрическое

Что такое Среднее геометрическое?

Среднее геометрическое – это среднее значение набора продуктов, расчет которого обычно используется среднее арифметическое работает с самими значениями.

Ключевые моменты

Формула для среднего геометрического

Понимание среднего геометрического

Например, вычисление среднего геометрического можно легко понять с помощью простых чисел, таких как 2 и 8. Если вы умножите 2 и 8, а затем извлечете квадратный корень (степень ½, поскольку имеется только 2 числа), ответ будет 4. Однако когда чисел много, их труднее вычислить, если не использовать калькулятор или компьютерную программу.

Краткая справка

Чем длиннее временной горизонт, тем более критичным становится сложное сложение и тем более подходящим является использование среднего геометрического.

Основное преимущество использования среднего геометрического состоит в том, что не нужно знать фактические инвестированные суммы; расчет полностью сосредоточен на самих цифрах возврата и представляет собой сравнение «яблок с яблоками» при рассмотрении двух вариантов инвестирования за более чем один период времени. Среднее геометрическое всегда будет немного меньше среднего арифметического, которое является простым средним.

Как рассчитать среднее геометрическое

Чтобы рассчитать сложные проценты с использованием среднего геометрического дохода от инвестиций, инвестору необходимо сначала рассчитать проценты в первом году, которые составляют 10 000 долларов, умноженные на 10%, или 1000 долларов. На второй год новая основная сумма составляет 11000 долларов, а 10% от 11000 долларов составляют 1100 долларов. Новая основная сумма теперь составляет 11000 долларов плюс 1100 долларов, или 12100 долларов.

На третий год новая основная сумма составляет 12 100 долларов, а 10% от 12 100 долларов составляют 1210 долларов. По прошествии 25 лет 10 000 долларов США превращаются в 108 347,06 долларов США, что на 98 347,05 долларов США больше первоначальных инвестиций. Более короткий путь состоит в том, чтобы умножить текущую основную сумму долга на единицу плюс процентную ставку, а затем поднять коэффициент до числа сложенных лет. Расчет: 10 000 долларов США

Источник

Когда применять среднее геометрическое: ключевые примеры

Что такое среднее геометрическое?

В статистике среднее геометрическое вычисляется путем возведения произведения ряда чисел до значения, обратного общей длине ряда. Среднее геометрическое наиболее полезно, когда числа в серии не независимы друг от друга или если числа имеют тенденцию к большим колебаниям.

Применение среднего геометрического наиболее распространено в бизнесе и финансах, где оно часто используется при работе с процентами для расчета темпов роста и доходности портфеля ценных бумаг.Он также используется в некоторых индексах финансовых и фондовых рынков, таких какгеометрический индекс линии ценностиFinancial Times.

Понимание среднего геометрического

Темпы роста

Среднее геометрическое используется в финансах для расчета средних темпов роста и называется совокупным годовым темпом роста. Рассмотрим акции, которые вырастают на 10% в первый год, падают на 20% во второй год, а затем вырастают на 30% в третий год. Среднее геометрическое значение скорости роста рассчитывается следующим образом:

В доходности портфеля

Среднее геометрическое обычно используется для расчета годовой доходности портфеля ценных бумаг. Рассмотрим портфель акций, который вырастает со 100 до 110 долларов в первый год, затем снижается до 80 долларов во второй год и поднимается до 150 долларов в третий год. Затем доходность портфеля рассчитывается как (150 долл. США / 100 долл. США) ^ (1/3) = 0,1447 или 14,47%.

В фондовых индексах

Среднее геометрическое также иногда используется при построении фондовых индексов.Многие из индексов Value Line, публикуемыхFinancial Times, используют среднее геометрическое.  В этом типе индекса все акции имеют равный вес, независимо от их рыночной капитализации или цен. Индекс рассчитывается путем взятия среднего геометрического пропорционального изменения цены каждой акции в составе индекса.

Корни в геометрии

Среднее геометрическое было впервые концептуализировано греческим философом Пифагором Самосским и тесно связано с двумя другими классическими средствами, прославившимися им: средним арифметическим и средним гармоническим.

Среднее геометрическое также используется для наборов чисел, где значения, умноженные вместе, являются экспоненциальными. Примеры этого явления включают процентные ставки, которые могут быть привязаны к любым финансовым инвестициям, или статистические ставки при росте населения.

Источник

Зачем нужно среднее геометрическое

…Однако давайте оглянемся на уже известное. Поговорим о среднем геометрическом. Разберемся в его отношениях. Ведь не случайно, наверное, оно постоянно возникает в нашем путешествии по Саду «Золотой пропорции». И оно же, возможно, нас выведет к какой-то теме. Здесь всё взаимосвязано, мы знаем…

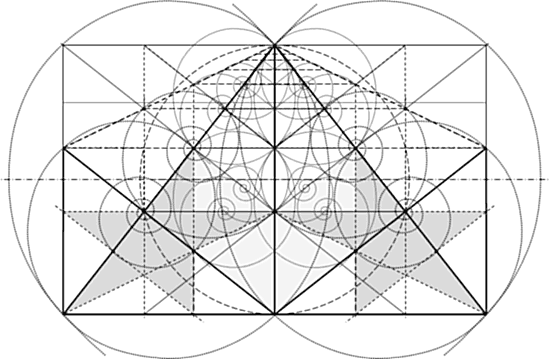
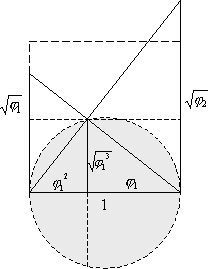
Посмотрите этот рисунок одной величины, как средне-геометрической. А в комментарии к нему становится понятен общий геометрический смысл.

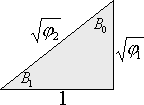
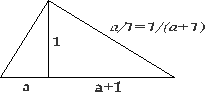
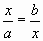
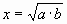
Или вот такой рисунок справа. Им задается квадратное уравнение для а= j ₁. Здесь b=a+1 и или . Как видите, здесь основная связь – средне-геометрическая…

Давайте посмотрим на ряд значений, образующих какую-то последовательность; посмотрим буквально – то есть «геометрически». Отложенные на линии величины чисел образуют «шкалу».

Любая шкала показывает характер изменения какого-то параметра. Если в природе происходит нарастание какого-то параметра, то оно происходит, обычно, равномерно по отношению к предыдущим значениям, то есть в определенном равномерном отношении, равномерном произведении. Изменение параметра по показательной функции будем называть «природной шкалой». То есть природная шкала – это какая-то показательная функция (экспонента) – для реальных значений какого-то параметра. Или по другому, природная шкала, как шкала значений показательной функции «y=a x », есть некая логарифмическая спираль. Логарифмическая спираль – образ природной шкалы. Беря логарифм от такой реальной природной шкалы, мы получаем для себя шкалу равномерного суммирования (x=log_aa x ).

Существует общая особенность нашего восприятия – логарифмическая шкала над реальным миром. Основанием восприятия громкости является «10», основанием для высоты звука – «2», основанием восприятия яркости – «

2,5»… Возьмем произвольную физическую шкалу степенных отрезков (a n ). Интересно отметить, что такая шкала степенных отрезков (a n ) заворачивается в логарифмическую спираль так, что эти отрезки размещаются между ортогональными осями (т.е. в ритме 90 ° ).

На нижнем рисунке сверху представлена некая «природная шкала» с коэффициентом j ₂ между соседними значениями. Штрихами на общей оси «закреплены» также члены ряда Фибоначчи «1-1-2-3».

На ней воочию видно, что шкала степенных значений j ₂ сдвинута по отношению шкалы ряда Фибоначчи так, что ее отметки (ее числа) делят целочисленный промежуток между отметками шкалы Фибоначчи по Золотой пропорции.

По «k» последовательным членам такой шкалы нам интересно знать их среднее геометрическое. Беря эти значения при возрастающем количестве последовательных членов (k), мы получим некий ряд.

Итак, общая формула среднего геометрического «природной шкалы»: 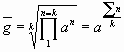. (Посмотрите на выражение степени. Это среднее арифметическое и является средним в логарифмической шкале, производной от нашей «природной».) И ниже представлена таблица, интересующей нас зависимости для средне-геометрического « g ».

Каждое следующее значение среднего геометрического отличается в Ц a. Наше a= j ₂ (или j ₁). На верхних рисунках мы видели постоянное «гуляние» по нему именно этих табличных выражений. То есть в сетке углов «B₀-B₁» постоянно (везде и всюду на углах B₀ и B₁) порождаются средние геометрические величины.

В тексте «О взаимообратных числах» была такая общая формула для выражения отношений, подобных Золотой пропорции:

Здесь D є m/t и, как известно, D =k₂–k₁. А для ЗП D =1. То есть ЗП возникает в отношениях отрезков со своим средним геометрическим, когда оно равно разности отрезков: 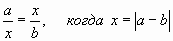. Из этой формулы заменой получается интересное уравнение: a 2 – 3ab + b 2 = 0, – с единственным решением в виде двух значений ЗП: j ₂ и j ₁ для «a» или «b».

Отношения ЗП – это особый случай среднего геометрического. И у нее свой треугольник Золотой пропорции – второй от начала этого текста. Но вот «Золотой треугольник» все же не он… (Им является или 1-ый, или равнобедренный с углом 36 ° в вершине.)

Построим таблицу разных значений «а» и «b» при условии, что их среднее геометрическое равно «1».

(Интересное соотношение из таблицы: .)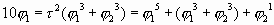

Данные этой таблицы помогают построить нижний левый рисунок. Для сравнения эти же треугольники построены на одной гипотенузе на правом рисунке.

Посмотрите на красивый левый рисунок с одинаковым средним геометрическим. В нем вырисовывается сторонами «b», как ограничивающими касательными, некая кривая. Что же за кривую (какой формулы) образуют эти большие стороны треугольников, как касательные к ней, так что она (кривая) формируется в их множестве минимальными ординатами для каждого «х»? Оформим математически этот сформулированный вопрос.

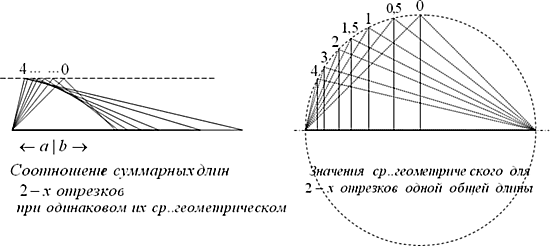
Это условие для всех «b» можно выразить так (через общее значение для ординаты):

.

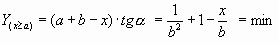
Возьмем производную и приравняем к «0» (для связи с минимальным значением):

.

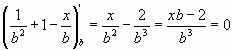
Получаем условие минимального значения функции: bx=2.

(Интересно то, что данную зависимость можно найти простым рассуждением, идя по исходному рисунку от треугольника (из множества) с b=1.)

Тогда можно составить уравнение: .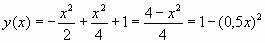

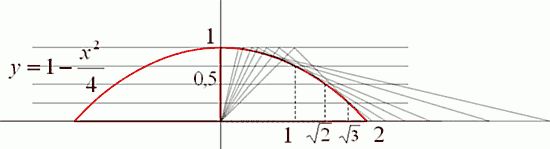
И построить точный график.

Какой может быть здесь связь с ЗП, которая связана одним своим коренным свойством (ab=1) со средним геометрическим? Эти отношения связаны с «четверками» или с «квадратами половинок». В этом структурное сходство с формулой Золотой пропорции:

.

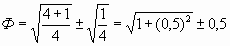
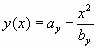
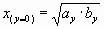
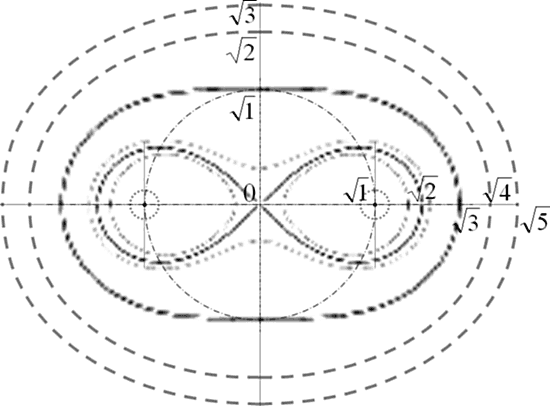
При этом в самом общем виде для параболы всегда выполняется такое среднее геометрическое соотношение: .

Мне же вспомнились овалы Кассини, формула (коэффициент) которых есть средне-геометрическое их радиус-векторов. Причем эта величина для каждого отдельного овала — постоянная…

Овалы Кассини меняют свою форму из-за изменения значения произведения радиус-векторов. Пограничные для разных типов овалов имеют таким произведением определенные значения относительно расстояния «а» между фокусами и центром. Лемниската – первая граничная кривая, срединная между эллипсовидными с «талией» и парными отдельными яйцевидными овалами (стремящимися к 2-м окружностям вокруг полюсов); ее r_{1 Ч} r₂=a 2 . Следующим граничным овалом за лемнискатой является овал с горизонтальными участками; его r_{1 Ч} r₂=( Ц 2 Ч a) 2 , отметка горизонтального участка y=a, максимальная абсцисса X_max= Ц 3 Ч a. Будем называть (при «а», отнесенном к «1») «коэффициентом овала» 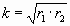, являющееся средним геометрическим радиус-векторов. Для лемнискаты k= Ц 1, для 2-го граничного овала k= Ц 2. Посмотрите на это семейство овалов Кассини.

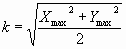
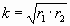
Из рисунка видно, что в овалах Кассини соотношение размеров по ортогональным осям строится «на квадратных корнях». Но это только часть видимого. Взаимосвязь через квадратный корень становится еще убедительнее в следующем выражении: . Здесь «k» – это по определению овалов то самое среднее геометрическое радиус-векторов: .

Приведем 3 формулировки этого интересного свойства (или правила) овалов Кассини.

Коэффициент овала равен квадратному корню из полу-суммы квадратов наибольших значений X и Y (точек пересечения с осями).

Коэффициент овала равен среднему квадратичному «габаритных» значений по X и Y.

Коэффициент овала равен равнобедренному катету от гипотенузы, проведенной между точками пересечения с осями X и Y.

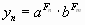
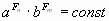
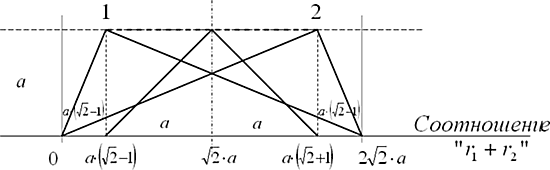
Кстати, в тексте «Гармония звуков..» был определен класс дискретных функций: , где F_n,m – числа Фибоначчи. Тогда здесь можно выделить класс линий . Овалы Кассини – это a 1 Ч b 1 = c. Не менее интересно было бы исследовать образы и других подобных линий-функций …

Мы можем построить на этой постоянной величине схему, в которой будет видно изменение и соотношение (пределы) радиус-векторов. Например, для лемнискаты (где ).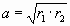

То есть множество прямоугольных треугольников, располагаясь вершинами на отрезке 1 ё 2, образует на основании проекциями катетов соотношение «r₁+r₂». Три треугольника на рисунке соответствуют (задают) по порядку крайней левой точке, центральной точке и крайней правой точке (на оси X).

Так что же за тайна в среднем геометрическом? Почему она так часто присутствует там, где гармония? Может быть этот треугольник Золотой спирали расставит все точки… (Он же — в овалах Кассини.) И это соотношение 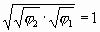… Этот треугольник – основа Золотого пространства, формируемого Золотыми спиралями.

Золотое пространство с-троит-ся на среднем геометрическом!

Остается, правда, один вопрос. Все наши «работающие» средние геометрические – это радикалы от 2-х элементов. Почему? И еще добавка к этому: в верхней таблице значений средне-геометрического по нескольким последовательным элементам природной шкалы эти значения вычисляются квадратным радикалом… Так все-таки, что причастно гармонии: квадратный радикал или любые средние геометрические. Для нее безразлична «мерность» или как-то она связана с «площадными» мерами.

Кстати, насчет квадратного корня. Евгений Скляревский, например, подсчитал, что получение точного значения Золотой пропорции по формуле приближения в виде бесконечных вложенных радикалов из «1» происходит быстрее в 1 1 /₃, чем по формуле бесконечной цепной дроби…

Текст закончился многоточием; вопросы остались. По прошествии времени я отправил его Виктору Белянину. К тому моменту Виктор успел системно изложить свои взгляды по истории Золотой пропорции. Ответ на мое «послание» не заставил себя ждать. В нем главной по теме была следующая фраза: «Сергей, ты пишешь, что я невольно сопоставляю ЗП и геометрическую прогрессию. Нет, я говорю о геометрической пропорции, а не о геометрической прогрессии. Это «две большие разницы»». И разговор получил продолжение.

Вроде бы обосновали физики, что материальный мир мог быть только 3-х мерным. Так все-таки случайна или нет «2-х мерность» гармонии в 3-х мерном мире.

Кстати, определение «деление отрезка в среднем и крайнем отношении» сформулировано Пачоли или Платоном? (Пары элементов любой пропорции так и называются: средние и крайние.) Если Платоном, то ведь построение геометрической пропорции на целостном отрезке и есть Золотое сечение… А?! Или он говорил только о величинах (числах)? Тогда получается, что, перейдя на отрезки, Пачоли и вышел на Золотое сечение…

И тогда: феномен ЗП превратился в явление, когда Кеплер первый (вроде бы) показал связь ЗП и аддитивного ряда… И ведь он же (вроде бы) привел привычное нам алгебраическое выражение для ЗП. У Пачоли оно было другое. Если все так, то прозрение ЗП – заслуга Пачоли (как и бух.учет), а научное осознание и победное шествие ЗП начинается с Кеплера.

1. Геометрическая пропорция: b 2 =ac. Непрерывная пропорция: a/b=b/c=c/d=d/e=. Называть геометрическую пропорцию непрерывной пропорцией не всегда корректно!

Далее. Прежде чем говорить, что у Платона есть геометрическая прогрессия, надо выяснить существовало ли тогда это понятие, строили ли тогда спирали (первую спираль построил, кажется, Архимед, живший значительно позже Платона). А просто так приписывать древним то, что нам хочется — это ошибка. Против этого я и выступаю, чтобы очищать ЗС от выдумок. Опираться надо на античные тексты, мыслить их категориями и их понятиями, а не сочинять что-либо в кабинетной тиши.

2. А кто тебе сказал, что гармония 2-х мерна? А трехмерной гармонии нет?

3. «Деление отрезка в среднем и крайнем отношении» сформулировано Евклидом.

4. Платон нигде (!) никаких (!) построений на целостном отрезке не выполняет! Не сочиняй! А если знаешь, где он это делает, то укажи мне это место.

5. «Величины» и «числа» в Древней Греции — это не одно и тоже! То, что можно было делать с величинами, никогда греки не делали с числами. Этому посвящены очень обширные статьи.

Помилуй. Да, я просто рассуждаю, причем для тебя. Рассуждаю от нынешнего уровня. И ничего не приписываю древним.

Я смотрю, не в тон попал. Теперь для сближения — по порядку.

(На 1). Не настаиваю. Но в отношении непрерывной пропорции взял из справочника.

Там она точь-в-точь геометрическая. Ты как бы более прав. Но согласимся, что геометрическая — это 1 звено цепочки непрерывной.

(На 2). Пропускаю. Без комментариев здесь. Хорошо бы при встрече.

(На 3). Евклид жил после Платона. Значит ЗC начинается с Евклида (неважно, как он это называл)… Или с древних архитекторов, которые использовали соответствующие меры-инструменты, хотя и не называли их термином, похожим на современный… Вообще, какой момент осмысления означает, что «принцип» осознан, то есть включен в общую систему знаний.

(На 4). Так я и не сочиняю, просто спрашиваю. Виктор, я вообще мало читал о ЗП у других авторов перед тем, как она меня увлекла.

(На 5). Этого я вообще не знаю. Я говорил от себя.

…Математика — вещь четкая.

(На 1). Все правильно. Если ты подразумеваешь в тексте одно звено, то надо писать геометрическая, если цепочку — то надо писать непрерывная. Должна быть строгая терминология. Я за это.

(На 3). «Евклид жил после Платона?»

Евклид жил после Платона спустя примерно 60-75 лет.

«Значит ЗC начинается с Евклида (неважно, как он это называл)».

ЗС с Евклида не начинается (так я считаю). Он решил задачу деления отрезка в крайнем и среднем отношении. Это был его промежуточный результат для других целей. Это совпадает с ЗС. Но того смысла в деление отрезка, который в это вкладываем мы, Евклид не вкладывал. Совпадение — да, смысл — нет. Прочти еще раз первую страницу моей статьи о Платоне.

(На 5). «Этого я вообще не знаю. Я говорил от себя».

Величины и числа в Древней Греции — это длинная история. Только краткий пример. Греки отрезок в пять единиц (величина) — делили пополам. Но число 5 они пополам не делили. Отношение 5:2 у них было, но дроби 5/2 у них не было.

Виктор, я хотел тебе привести для проверки фразу «Величина измеряется числом». После твоей ремарки надо сказать (дополнить), что «понимание величины и числа — самостоятельно и исторично».

Вообще, твоя статья «о Платоне и ЗП» мне очень нравится. Проникновение и в букву, и в дух (то есть в эпоху, в мировоззрение и т.д.) древних текстов, конечно необходимо, чтобы делать правильные выводы. И это интересно. И ты правильно делаешь. В книге (в отличие от статьи) же нужно меньше споров с современниками, это отвлекает.

История ЗП — тема благодарная. Хотя бы на моем примере. Я не углублялся в историю. Но надо подходить к ней именно так: разделяя, понимая и собирая вновь «дух и букву», смысл и текст.

Ты прав — надо четко разделять ЗП и ее историю, где много и много сказочного.

Никто до сих пор ее историей серьезно не занимался. Многие же увлеклись обаянием ЗП и насочиняли.

Два с лишним года копания в истории математики и философии привели меня к выводу, что нельзя сегодняшними мерками оценивать древних. Нельзя им приписывать из конъюнктурных соображений лишних знаний. Они не одно столетие (!) решали задачу х 3 = 2а 3 (удвоение куба). Сейчас это решается за минуту…

К этому времени мне уже получилось посмотреть «дискуссию» на тему истории ЗП на новосибирском сайте «a3d». Эмоциональное самовыражение, часто переходящее в стёб. Да это и неизбежно в формате, когда все сразу не скажешь… Конечно, эмоциональное заводит. И может служить катализатором дальнейших поисков и писаний. Лишь бы не остался турнирный «захлест». Но главное – уровень слышания оппонента и отношения друг к другу. А вот здесь и проблемы. И польза здесь от разговора – стремящаяся к нулю.

Как неприятно смотреть на такие «научные споры», где расчет идет на подавление оппонента, на уничтожение. Какая уж там истина; она становится сразу средством. В этой «политике» прикрываются неким «великим предметом спора» и делают свою позицию и себя присвоением его. А противника в споре (уже – противника) – выставляют противником самого «великого предмета». Политика…

Так получается и в споре об исторических аспектах Золотой пропорции. В этом разговоре очень важна четкость позиций. Спорят-то люди. ЗП здесь ни при чем. Важно четко разделить саму ЗП, ее историю, и тем более толкование истории.

Необходима книга, которая расчистит многое, связанное с Золотой пропорцией… Нужна книга о ЗП, в которой совершенно «по-олимпийски», без влияния эмоций и споров, кто-то попытается упорядочить и историю, и багаж знаний о ЗП. В том числе и в терминах.

В запале спора Виктор Белянин пишет так, что можно его представить противником просвещения. Если захотеть… Как и А.П. Стахов, я считаю необходимым привнесение ЗП в учебный процесс средней школы. Виктор по его словам тоже сторонник привнесения ЗП в школьный предмет по математике. «О ЗП необходимо писать в учебниках по математике! В учебниках, а не устраивать из нее шоу в виде отдельного предмета. Школьники и так перегружены мутью в разных предметах. Это я знаю, т.к. иногда для знакомых занимаюсь с их детьми по математике, химии и физике. ЗП — это красивая задача, но о ней достаточно рассказать на 1-2 уроках, а дальше каждый сам решит, углубляться в ее тему или нет. Такое мое мнение. Красивых задач в математике много, а гармония и красота не обязательно связаны с ЗП, скорее, может быть, даже, и не связаны. Это два таинства и разгадать их никогда не удастся, особенно с помощью чисел. Подойти близко можно, но разгадать по пифагорейски, с помощью чисел – никогда».

Здесь можно поставить очередное многоточие. Мое новое несогласие с Виктором здесь носит, очевидно, «вкусовой характер», оно бездоказательно. Оно построено на внутреннем ощущении и не имеет (пока) рациональных аргументов, приемлемых и убедительных для другой стороны. Набор (подборка) отдельных фактов в онтологическом осмыслении – это лишь «руда», а не кристаллы истины. Придёт время…

Источник