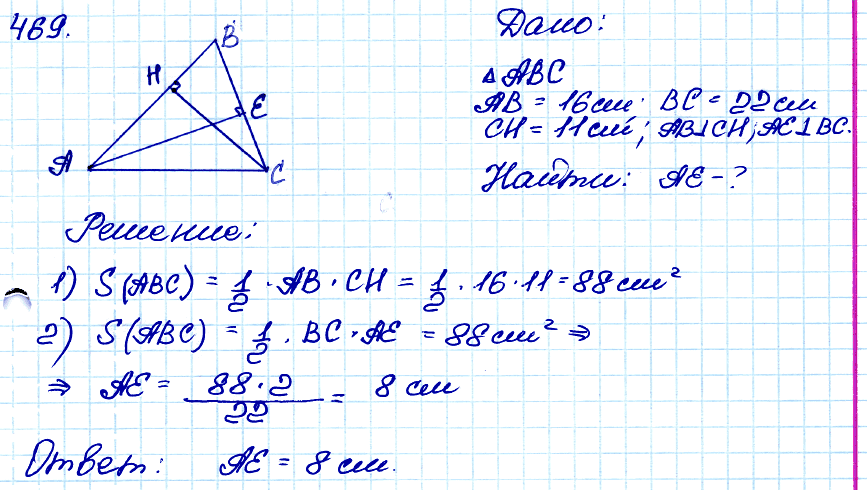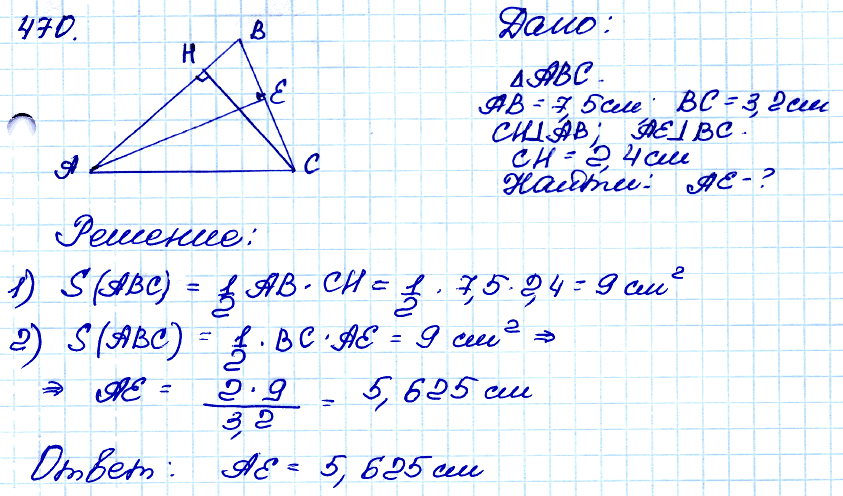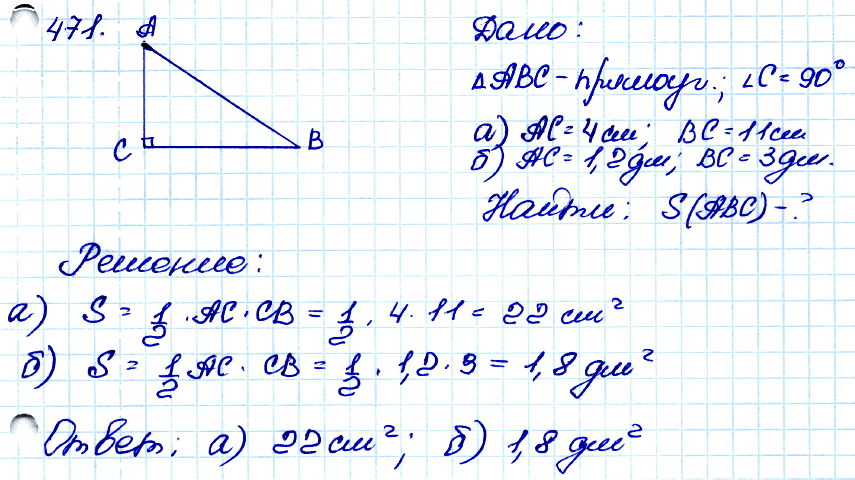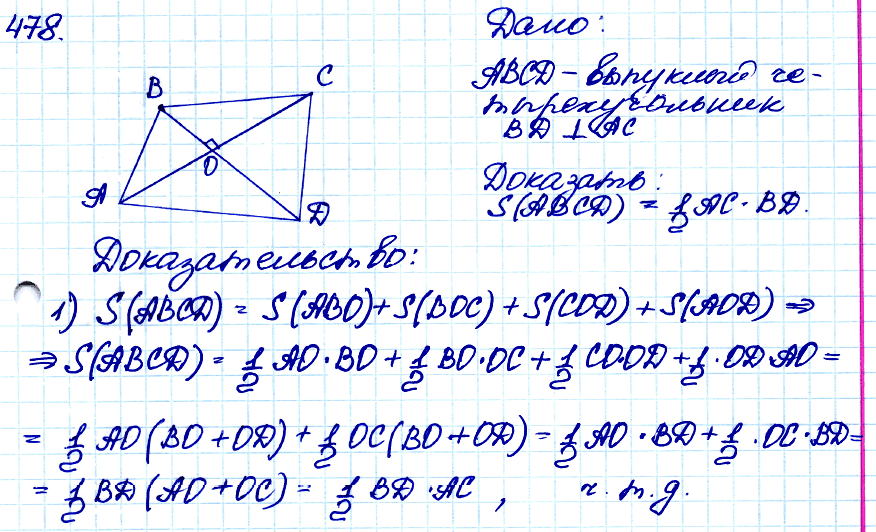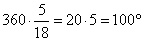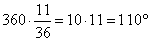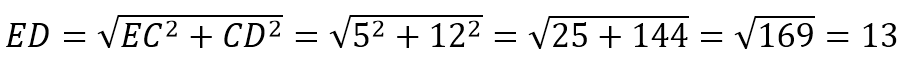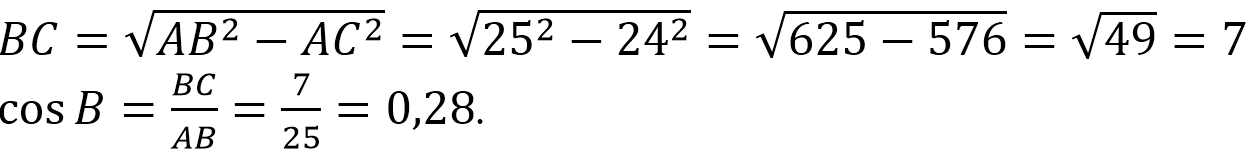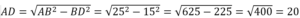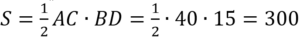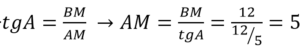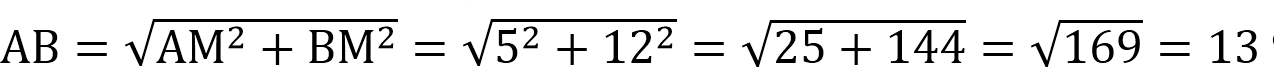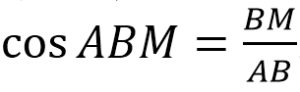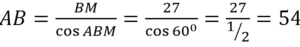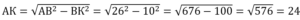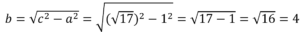Высоты треугольника равны 12 15 и 20 доказать что треугольник прямоугольный
Высоты, проведенные из вершин А, В и С треугольника АВС, равны 20, 15 и 12 соответственно?
Высоты, проведенные из вершин А, В и С треугольника АВС, равны 20, 15 и 12 соответственно.
А) Докажите, что треугольник АВС прямоугольный.
Б) Найдите длину биссектрисы треугольника, проведенной из вершины С.
В прямоугольном треугольнике две высоты совпадают с катетами, это 20 и 15.
Тогда гипотенуза c = (20 ^ 2 + 15 ^ 2) ^ (1 / 2) = 25, высота, опущенная на с Hc = ab / c = 12 данная в условии.
Искомаябиссектриса bc, проведенная извершины прямого угла C выражается известной формулой
bс = 2b * a * cos(π / 4) / (a + b) = 2 * 15 * 20 / 1, 41 * (15 + 20).
В треугольнике АВС углы А и В равны соответственно 45 градусов и 67 градусов?
В треугольнике АВС углы А и В равны соответственно 45 градусов и 67 градусов.
Найдите угол между биссектрисой и высотой, проведенными из вершины С.
Ответ дайте в градусах.
Катеты АС и ВС прямоугольного треугольника АВС относятся как 3 : 4 соответственно?
Катеты АС и ВС прямоугольного треугольника АВС относятся как 3 : 4 соответственно.
Найти высоту прямоугольного треугольника, проведенную из вершины прямого угла, если гипотенуза равна 20.
Решите пожалуйста?
Катеты АС и ВС прямоугольного треугольника АВС относятся как 6 : 8 соответственно.
Найдите высоту прямоугольного треугольника, проведенную из вершины угла, если гипотенуза равно 30.
Докажите, что треугольник АВС равнобедренный, и найдите высоту треугольника проведенную из вершины А.
Докажите что у равных треугольников авс и а1в1с1 биссектрисы, проведенные из вершин а и а1, равны?
Докажите что у равных треугольников авс и а1в1с1 биссектрисы, проведенные из вершин а и а1, равны.
Катеты АС и ВС прямоугольного треугольника АВС относятся как 6 : 8 соответственно?
Катеты АС и ВС прямоугольного треугольника АВС относятся как 6 : 8 соответственно.
Найдите высоту прямоугольного треугольника, проведенную из вершины прямого угла, если гипотенуза равна 30.
Докажите, что у равных треугольников АВС и А1В1С1 медианы, проведенные из вершин А и А1 равны?
Докажите, что у равных треугольников АВС и А1В1С1 медианы, проведенные из вершин А и А1 равны.
Высота и медиана, проведенные из вершины B треугольника АВС, делят угол на три равные части?
Высота и медиана, проведенные из вершины B треугольника АВС, делят угол на три равные части.
Найдите углы треугольника АВС.
Докажите, что треугольник равнобедренный, и найдите высоту треугольника проведенную из вершины А.
В треугольнике АВС углы А и С равны 20° и 60° соответственно?
В треугольнике АВС углы А и С равны 20° и 60° соответственно.
Найдите угол между высотой и биссектрисой, проведенными из вершины В.
Геометрия 8 класс Атанасян Задачи 459-482
Упражнения 459-482 из учебника «Геометрия 8 класс. УМК Атанасян» с ответами и решениями. Глава VI. Площадь. § 2. Площади параллелограмма, треугольника и трапеции (52. Площадь параллелограмма. 53. Площадь треугольника. 54. Площадь трапеции). Геометрия 8 класс Атанасян Задачи 459-482 + ОТВЕТЫ.
Нажмите на спойлер, чтобы посмотреть ответ на задание.
Геометрия Атанасян. Глава 6.
§ 2. Площади параллелограмма,
треугольника и трапеции
Задачи №№ 459-482:
Задача № 460. Диагональ параллелограмма, равная 13 см, перпендикулярна к стороне параллелограмма, равной 12 см. Найдите площадь параллелограмма.
Задача № 461. Смежные стороны параллелограмма равны 12 см и 14 см, а его острый угол равен 30°. Найдите площадь параллелограмма.
Задача № 462. Сторона ромба равна 6 см, а один из углов равен 150°. Найдите площадь ромба.
Задача № 463. Сторона параллелограмма равна 8,1 см, а диагональ, равная 14 см, образует с ней угол в 30°. Найдите площадь параллелограмма.
Задача № 465. Острый угол параллелограмма равен 30°, а высоты, проведённые из вершины тупого угла, равны 2 см и 3 см. Найдите площадь параллелограмма.
Задача № 466. Диагональ параллелограмма равна его стороне. Найдите площадь параллелограмма, если большая его сторона равна 15,2 см, а один из его углов 45°.
Задача № 467. Квадрат и ромб, не являющийся квадратом, имеют одинаковые периметры. Сравните площади этих фигур.
Задача № 469. Стороны АВ и ВС треугольника АВС равны соответственно 16 см и 22 см, а высота, проведённая к стороне АВ, равна 11 см. Найдите высоту, проведённую к стороне ВС.
Задача № 470. Две стороны треугольника равны 7,5 см и 3,2 см. Высота, проведённая к большей стороне, равна 2,4 см. Найдите высоту, проведённую к меньшей из данных сторон.
Задача № 471. □ Найдите площадь прямоугольного треугольника, если его катеты равны: а) 4 см и 11 см; б) 1,2 дм и 3 дм.
Задача № 473. Через вершину С треугольника АВС проведена прямая m, параллельная стороне АВ. Докажите, что все треугольники с вершинами на прямой m и основанием АВ имеют равные площади.
Задача № 474. Сравните площади двух треугольников, на которые разделяется данный треугольник его медианой.
Задача № 475. □ Начертите треугольник АВС. Через вершину А проведите две прямые так, чтобы они разделили этот треугольник на три треугольника, имеющие равные площади.
Задача № 476. Докажите, что площадь ромба равна половине произведения его диагоналей. Вычислите площадь ромба, если его диагонали равны: а) 3,2 дм и 14 см; б) 4,6 дм и 2 дм.
Задача № 478. В выпуклом четырёхугольнике диагонали взаимно перпендикулярны. Докажите, что площадь четырёхугольника равна половине произведения его диагоналей.
Задача № 480. Найдите площадь трапеции ABCD с основаниями АВ и CD, если:
а) АВ = 21 см, CD = 17 см, высота ВН равна 7 см;
б) ∠D = 30°, АВ = 2 см, CD = 10 см, DA = 8 см;
в) ВС ⊥ АВ, АВ = 5 см, ВС = 8 см, CD = 13 см.
Задача № 481. Найдите площадь прямоугольной трапеции, у которой две меньшие стороны равны 6 см, а больший угол равен 135°.
Задача № 482. Тупой угол равнобедренной трапеции равен 135°, а высота, проведённая из вершины этого угла, делит большее основание на отрезки 1,4 см и 3,4 см. Найдите площадь трапеции.
Вы смотрели: Упражнения из учебника «Геометрия 8 класс. УМК Атанасян» с ответами и решениями. Глава VI. Площадь. § 2. Площади параллелограмма, треугольника и трапеции (52. Площадь параллелограмма. 53. Площадь треугольника. 54. Площадь трапеции). Геометрия 8 класс Атанасян Задачи 459-482 + ОТВЕТЫ.
Задание №15 ЕГЭ по математике базового уровня
Планиметрия
В задании № 15 базового уровня ЕГЭ по математике нас ждет решение задач по планиметрии. Задачи в этом разделе не сложные, достаточно знать определения основных понятий и базовые формулы, после чего задача сводится к элементарным вычислениям.
Разбор типовых вариантов заданий №15 ЕГЭ по математике базового уровня
Вариант 15МБ1
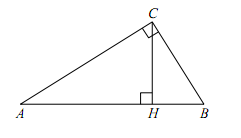
В треугольнике ABC угол ACB равен 90°, cos A = 0,8, AC = 4. Отрезок CH – высота треугольника ABC(смотрите рисунок). Найдите длину отрезка AH.
Алгоритм выполнения:
Решение:
Вспомним определение косинуса угла.
Косинус – это тригонометрическая функция, которая в прямоугольном треугольнике обозначает отношение катета, прилежащего к острому углу, к гипотенузе.
Запишем выражение для нахождения косинуса угла. Для этого рассмотрим треугольник ACH.
Гипотенуза – это сторона прямоугольного треугольника, лежащая против угла 90°. В данном случае против угла H лежит сторона AC, то есть AC – гипотенуза.
Прилежащий к углу А катет – АН.
Получим cos A = АН/АС.
Выразим неизвестную величину.
АН = АС · cos A = 4 · 0,8 = 3,2
Вариант 15МБ2
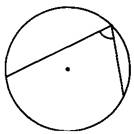
Найдите вписанный угол, опирающийся на дугу, длина которой равна 5/18 длины окружности. Ответ дайте в градусах.
Алгоритм выполнения:
Решение:
Вспомним соотношение величины вписанного угла и градусной меры угла, на который он опирается.
Величина вписанного угла равна половине градусной меры дуги, на которую он опирается.
Вычислим градусную меру угла, на который опирается дуга.
Весь круг составляет 360°, а 5/18 от его длины это
Вычислим вписанный угол.
Так как вписанный угол равен половине градусной меры дуги, на которую он опирается, вписанный угол равен
Вариант 15МБ3
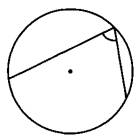
Найдите вписанный угол, опирающийся на дугу, длина которой равна 11/36 длины окружности. Ответ дайте в градусах.
Алгоритм выполнения:
Решение:
Вспомним соотношение величины вписанного угла и градусной меры угла, на который он опирается.
Величина вписанного угла равна половине градусной меры дуги, на которую он опирается.
Вычислим градусную меру угла, на который опирается дуга.
Весь круг составляет 360°, а 11/36 от его длины это
Вычислим вписанный угол.
Так как вписанный угол равен половине градусной меры дуги, на которую он опирается, вписанный угол равен
Вариант 15МБ4
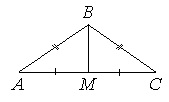
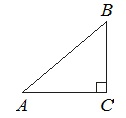
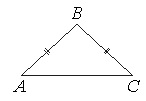
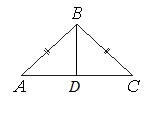
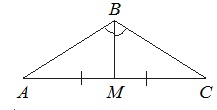
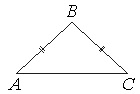
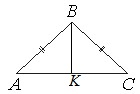
В треугольнике АВС известно, что АВ=ВС=15, АС=24. Найдите длину медианы ВМ.
Алгоритм выполнения
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Решение:
Если АВ=ВС, то ∆АВС – равнобедренный.
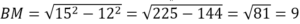
Вариант 15МБ5
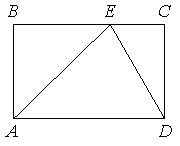
На стороне ВС прямоугольника АВСD, у которого АВ=12 и АD=17, отмечена точка Е так, что треугольник АВЕ равнобедренный. Найдите ЕD.
Алгоритм выполнения
Решение:
Т.к. по условию ∆АВЕ равнобедренный, то ВЕ=АВ=12.
Т.к. АВСD прямоугольник, то ВС=АD=17, СD=АВ=12.
Вариант 15МБ6
Алгоритм выполнения
Решение:
Вариант 15МБ7
В равнобедренном треугольнике АВС боковая сторона АВ=25, sin A=3/5. Найдите площадь треугольника АВС.
Алгоритм выполнения
Решение
В ∆ADB угол А является противолежащим к BD. Поэтому sin A=BD/AB → BD = AB · sin A = 25 · 3 / 5 = 15.
Из ∆ADB по т.Пифагора имеем: AB 2 =AD 2 +BD 2 →
Т.к. ∆АВС равнобедренный, то высота BD, проведенная к основанию, является и медианой. Поэтому АС=2АD=2·20=40.
Вариант 15МБ8
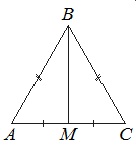
В равнобедренном треугольнике АВС медиана ВМ, проведенная к основанию, равна 12, а tg А=12/5. Найдите длину боковой стороны треугольника АВС.
Алгоритм выполнения
Решение:
Т.к. ∆АВС равнобедренный, то медиана ВМ, проведенная к основанию, является и высотой. Тогда ∆АВМ прямоугольный.
Из ∆АВМ по теореме Пифагора АВ 2 =АМ 2 +ВМ 2 →
Вариант 15МБ9
Алгоритм выполнения
Решение:
По условию угол АВМ равен половине угла В. Значит, угол АВМ составляет
Т.к. ВМ – медиана, опущенная на основание равнобедренного ∆АВС, то ВМ является и высотой. Поэтому ∆АМВ прямоугольный с прямым углом АМВ.
В прямоугольного ∆АМВ:
Вариант 15МБ10
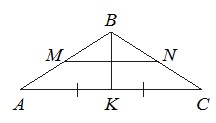
В равнобедренном треугольнике АВС медиана ВК=10, боковая сторона ВС=26. Найдите длину отрезка МN, если известно, что он соединяет середины боковых сторон.
Алгоритм выполнения
Решение:
Поскольку ВК медиана, то АС=2АК=2·24=48.
Линия, соединяющая в треугольники середины двух сторон, называется средней линией. Ее величина составляет половину третьей стороны (которой она параллельна).
Вариант 15МБ11
В треугольнике АВС высота АС=56, ВМ – медиана, ВН – высота, ВС=ВМ. Найдите длину отрезка АН.
Алгоритм выполнения
Решение:
Рассмотрим ∆АВС. Т.к. ВМ медиана, то АМ=МС=АС/2=56/2=28.
По условию ВС=ВМ, поэтому ∆МВС равнобедренный с основанием МС и равными боковыми сторонами ВМ и ВС. Тогда высота, проведенная к основанию, является еще и медианой. Отсюда следует, что МН=НС=МС/2=28/2=14.
Вариант 15МБ12
Найдите площадь прямоугольного треугольника, если его гипотенуза равна √17, а один из катетов равен 1.
Алгоритм выполнения
Решение:
Обозначим 1-й (известный) катет через а, 2-й – через b, гипотенузу – через с.
Т.к. треугольник прямоугольный, то его площадь можно найти по ф-ле: S=a·b/2. Тогда: S=1·4/2=2.
Вариант 15МБ13
В равнобедренном треугольнике АВС основание АС равно 32, площадь треугольника равна 192. Найдите длину боковой стороны АВ.
Алгоритм выполнения
Решение:
Площадь треугольника определяется по ф-ле: S=ah/2, где а=АС=32. Отсюда находим высоту ВК: BK=h=2S/a → ВК=2·192/32=12.
Т.к. ∆АВС равнобедренный, то высота, опущенная в нем на основание, является и медианой. Тогда АК=АС/2=32/2=16.
Высоты треугольника равны 12 15 и 20 доказать что треугольник прямоугольный
В остроугольном треугольнике ABC проведены высоты AM и CN.
А) Докажите, что углы ACB и MNB равны.
Б) Вычислите длину стороны АС, если известно, что периметр треугольника ABC равен 25 см, периметр треугольника BMN равен 15 см, а радиус окружности, описанной около треугольника BMN равен 3 см.
А) Рассмотрим прямоугольные треугольники AMB и CNB, у которых В — общий острый угол.
В ΔAMB: В ΔCNB:
Откуда:
Итак, в треугольниках MNB и ACB: угол В, заключенный между пропорциональными сторонами, общий. Это значит, что ΔMNB
ΔACB, откуда ∠ACB = ∠MNB, что и требовалось доказать.
Б) Известно, что у подобных треугольников периметры относятся как соответствующие стороны. Следовательно,
где k — коэффициент подобия названных треугольников.
Если то непременно
По следствию из теоремы синусов:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б. | 3 |
| Получен обоснованный ответ в пункте б. Имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. | 2 |
| Имеется верное доказательство утверждения пункта а. При обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки.
|