примеры 5 класс по математике для тренировки с ответами 4 четверть
Примеры 5 класс по математике для тренировки с ответами 4 четверть
Тестовые задания для 5 класса по 4 четверти.
Правильный вариант ответа отмечен знаком +
1. Напишите выражение: вычтите 4 из 18, а затем разделите на 7.
2. Какая цифра стоит в сотых долях числа 564391?
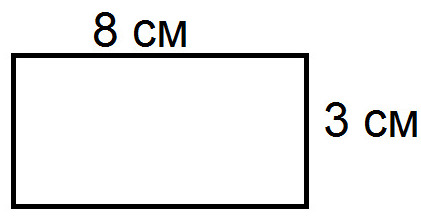
3. Можно ли определить объем этой фигуры?
— Да потому что это замкнутая форма
— Нет, потому что эта форма не дает достаточно информации, чтобы найти объем
— Да, потому что мы знаем длину каждой стороны
+ Нет, потому что эта форма плоская
4. Два угла называются смежными, если:
+ у них одна общая сторона, а две другие являются продолжениями одна другой
— их сумма равна 180 градусам
— стороны одного угла являются продолжениями сторон другого
5. В первый день похода школьники преодолели на лыжах путь в 27,5 км, во второй день они прошли на 1,3 км больше, чем в первый. А уже в среду школьники прошли в 1,2 раза меньше, чем во второй день. Сколько всего километров прошли школьник за три дня похода?
6. Выберите уравнение, которое отражает следующую фразу: сначала сложите 52 и 10, затем умножьте на 3.
7. В яблоневом саду собрали 8400 кг яблок. На долю антоновских яблок приходится 45% всего урожая. Сколько килограммов антоновских яблок собрали в саду?
8. Решите уравнение х: 0,6 = 0,43.
9. Отметьте ответ где: 3 однозначных числа и 2 двузначных числа.
тест 10. Решите уравнение 4,2у + 0,3у = 13,5.
11. Выполните деление 14,7 : 0,6.
12. Сколькими способами можно выбрать капитана команды и его заместителя из 5 человек?
13. В чем основное отличие треугольника от прямоугольника?
+ выходит из вершины угла и делит его на два равных угла
— выходит из вершины угла и проходит между его сторонами
— выходит из вершины угла и проходит во внутренней области угла
— делит угол пополам
16. Выразите в килограммах 0,008 т.
17. Дима помогал Диане раскладывать ее коллекцию марок в альбом. У Дианы целых 105 марок. Но на одну страницу альбома помещается всего 3 марки. Сколько разворотов в альбоме потребуется, чтобы разместить все марки, которые есть у Дианы? Учтите, что на первой странице марки помещать нельзя, а на последней их расположено только 3.
18. Найдите значение выражения: 0,4 + 1,85 : 0,5.
19. Выберите число, которое завершает уравнение: 21 561,72
Тест по математике для 5 класса за 4 четверть
Всероссийский конкурс для учителей математики
«10 главных вопросов»
Хубатуллина мадина Талгатовна
5 класс. Тест по математике за IV четверть.
а)380; б)254; в)57,9; г) 469
а)490; б) 507; в) 211; г) 10,5
а) 15,94; б) 16,0; в) 15,95; г) 15,9
а) 13,84; б) 13,83; в)13,87; г) 13,9
3. Найти значение выражения:
17,39 : (15-14,26) – 6 : 12,5.
а)40,25; б) 23,02; в)13,46; г)31,07
а)56,12; б)32,06; в) 31,86; г) 15,54
4.Найдите среднее арифметическое чисел :
32,7 ; 14,8 ; 15,3 ; 21,6.
а) 10,7; б) 31; в) 5,79; г) 21,1
а) 11,93; б) 3,28; в) 17,25; г) 3,37
5. Решите уравнение:
а) 56,15; б) 31,5; в) 40,5; г) 37,5
а) 24,35; б) 35,7; в) 1,5; г) 62,5
6. Найти значение выражения:
1,2х + 5,4х + 3,7х +2,5х, если х=100.
а) 12,80; б) 128; в) 1280; г) 0,1280
а) 0,920; б) 9200; в) 920; г) 9,20
а)11,9 ; б)7,96 ; в) 4,8 ; г) 9,6
а)4,6 ; б)17,9 ; в) 5,8 ; г) 6,6
а) 200; б) 128; в) 430; г)
Ученик решил 17 задач, что составляет 25% всех задач. Сколько задач нужно решить ученику?
а) 45; б) 68; в) 16; г) 83
В треугольнике АВС угол А = 35°, угол В=60°. Найдите градусную меру угла С.
а)75° ; б) 85° ; в) 65° ; г) 90°
В треугольнике КСВ угол К = 110°, угол С=20°. Найдите градусную меру угла В.
а)45° ; б)75° ; в) 50° ; г) 65°
угол САД = 55° и угол КЕМ = 115°
угол МАР= 45° и угол ДЕМ = 105°
Ответы к диагностическим работам УМК Виленкин
Спецификация КИМ для проведения тестовой работы по математике в 5 классе
1. Назначение КИМ – оценить уровень обученности обучающихся 5-х классов по предмету математика за IV четверть.
2. Документы, определяющие содержание КИМ. Содержание тестовой работы определяется на основе Федерального государственного образовательного стандарта основного общего образования (приказ Министерства образования и науки РФ от 17.12.2010г. № 1897 «Об утверждении федерального государственного образовательного стандарта основного общего образования»).
3. Характеристика структуры и содержания КИМ.
Каждый вариант тестовой работы состоит из 10 заданий, различающихся формой и уровнем сложности.
В работе предложены следующие разновидности заданий:
— 9 заданий с выбором ответа из четырёх предложенных и 1 задание на построение, причём на задания 1 – 4 ученику необходимо выбрать букву из четырёх предложенных и 6 заданий, для которых учащиеся должны написать решение с полным обоснованием.
4. Распределение заданий КИМ по содержанию и видам деятельности. В тестовую работу включены вопросы, проверяющие: сформированность понятийного аппарата по проверяемым разделам содержания; знание основных правил и формул. Умение их применять; умение оценивать логическую правильность рассуждений. Умение интерпретировать знаково-символьную информацию; умение применять изученные понятия, результаты, методы для решения задач практического характера, пользоваться оценкой и прикидкой при практических расчётах.
5. Время выполнения работы и условия её проведения. На выполнение работы отводится 40 минут. В заданиях с выбором ответа в бланке ответов рядом с номером задания ученик указывает букву, которая соответствует выбранному им ответа, в заданиях с полным обоснованием решения ученик приводит полное решение задания на листе бумаги и записывает букву ответа.
Контрольная работа по математике для 5 класса, 4 четверть. Проценты и углы.
Вариант 1.
1. Решите задачу:
Витя прочитал 100 страниц из книги, при этом ему осталось прочитать в 1,5 раза больше. Сколько процентов книги прочел Витя? Сколько процентов ему осталось проесть?
2. Решите задачу:
Стоимость книги, сначала увеличили на 20%, а потом снизили на 15 рублей. Сколько стоила книга сначала, если теперь она стоит 225 рублей?
3. Выполните задание:
В треугольнике ABC угол ∠A равен 48°, угол ∠B равен 32°. Постройте треугольник ABC. Чему равен угол ∠C? Чему равна сумма всех углов треугольника?
4. Решите задачу:
5. Логическая задача:
Пенсию дедушки увеличили на 50%, а пенсию бабушки на 60%. Означает ли это, что бабушка получит большую прибавку к пенсии?
Вариант 2.
1. Решите задачу:
В магазине до обеда было продано 60 кг муки, а осталось в 1,5 раза больше, чем продано. Сколько процентов всей муки было продано до обеда? Сколько процентов муки осталось в магазине?
2. Решите задачу:
Благодаря оптимизации производственного процесса, себестоимость одной единицы продукции уменьшилась на 25%, а потом еще на 10 рублей. Какова была начальная себестоимость продукции, если сейчас она составляет 170 рублей?
3. Выполните задание:
У треугольника AOD угол ∠A = 60° угол ∠O = 42°. Постройте треугольник AOD. Чему равен угол ∠D? Чему равна сумма всех углов треугольника?
4. Решите задачу:
5. Логическая задача:
Стоимость тетради увеличилась на 20%, а стоимость альбома увеличилась на 15%. Означает ли это, что надбавка на стоимость тетради больше, чем на стоимость альбома?
Задания по математике 5 класс: для занятий дома
Самостоятельные занятия с ребенком в домашних условиях играют важную роль в процессе обучения. Даже не имея специального образования можно самостоятельно прорешивать с ним примеры и задачи по основным темам, встречающимся в текущем учебном году.
Эти задания вы можете распечатать на принтере.
§ Как правильно заниматься дома
Для того чтобы занятия действительно приносили пользу, необходимо придерживаться определенных правил, которые помогут сделать день продуктивнее, без утомления ребенка:
§ Задания для 5 класса на тему «Натуральные числа»
Перед тем как познакомиться с обыкновенными и десятичными дробями, необходимо вспомнить что такое натуральные числа. Ими называются числа, используемые в повседневной жизни, например для счета предметов.
✍ 3адание 1
Определить, какое число стоит перед:
Определить, какое число на две единицы больше, чем:
✍ 3адание 2
Написать в виде словосочетаний следующие цифры:
✍ 3адание 3
Представить в виде чисел словосочетания:
§ 3адания на тему «Сравнения натуральных чисел»
При помощи сравнения можно определить какое из чисел меньшее, а какое большее. Те что меньше, стоят при счете раньше, чем те, что больше.
✍ 3адание
Расставить 3наки « » или «=» между числами:
§ 3адания на тему «Сложение, вычитания натуральных чисел»
✍ 3адание 1
Для того чтобы повторить сложение, вычитание чисел, а также порядок действий при вычислении сложного выражения, можно решить несколько выражений:
Ответ: 1) 3 792, 2) 2 755, 3) 6 946, 4) 993.
✍ 3аданиие 2
В саду росло 208 фруктовых деревьев. Яблонь и слив было 129 штук, а слив и груш — 115. Сколько яблонь росло в саду? Слив? Груш?
Решение: Если известно, что всего деревьев было 208, а яблонь и слив – 129, то можно вычислить количество груш.
1 действие: 208 – 129 = 79 грушевых деревьев.
Стало известно количество грушевых деревьев, значит можно узнать, сколько было слив.
2 действие: 115 – 79 = 36 сливовых деревьев.
После того, как стало известно, сколько было груш и слив, можно высчитать количество яблонь.
3 действие: 208 – (79 + 36) = 93 яблонь.
Ответ: В саду росло 93 яблони, 79 груш и 36 слив.
§ 3адания на тему «Луч, прямая, отрезок»
Отрезком называется часть прямой ограниченная двумя точками, его длинной считается расстояние между крайними точками. Луч — это часть прямой, которая состоит из точки и всех других точек, лежащих по одну сторону от нее.
✍ 3адание 1
Начертите отрезок АВ, равный 12 см. Отметьте на нем точки по порядку С и D так, чтобы отрезок АС был равен 4 см, а СD — 6 см. Вычислите, чему равен отрезок DВ?
Ответ: 12 — (4 + 6) = 2 см.
✍ 3адание 2
Начертите произвольную прямую и отметьте на ней два точки А, В и С так, чтобы длина отрезка АВ была 7 см, а отрезка ВС — 4 см. Какова длина отрезка АС?
Ответ: 7 + 4 = 11 см.
§ 3адания на тему «Уравнения»
Уравнением называется равенство, в котором один или несколько компонентов являются неизвестными.
✍ 3адание 1
Решить уравнения
Ответ: 1) x=7, 2) х=6, 3) х=3, 4) х=-2,5, 5) х=5.
✍ 3адание 2
Насте 12 лет, что на 4 года меньше, чем возраста Лены. Сколько лет Лене? Решить уравнением.
Решение: Возьмем возраст Лены за x, в таком случае можно составить уравнение:
x – 4 = 12,
х = 12 + 4 = 16.
Ответ: Лене 16 лет.
✍ 3адание 3
Велосипедист за 3 дня проехал 117 км. Какое расстояние он преодолел в первый день, если в последующие два дня он проезжал на 4 км больше, чем в предыдущий? Какое расстояние он преодолел во 2-й и 3-й дни?
Решение: Расстояние которое проехал велосипедист за 1-й день, возьмем за x. В таком случае, второй день будет выглядеть как: x + 4, а третий: (х + 4) + 4.
Можно составить уравнение:
1 день 2 день 3 день
х + (х + 4) +( х + 4 + 4) = 117
3х + 12 = 117
3х = 117 – 12 = 105
х = 105: 3 = 35.
Проверка: 35 + 35 + 4 + 35 +4 + 4 = 117
Ответ: В первый день велосипедист проехал 35 км. Во 2-й день: 35 + 4 = 39 км. В 3-й день: 35 + 4 + 4 = 43 км.
§ 3адания на тему «Квадрат и куб числа»
Квадратом числа называется произведение этого числа самого на себя. Куб — произведение числа самого на себя два раза.
✍ 3адание 1
Найти квадрат чисел:
Ответ: 1) 25, 2) 81, 3) 169, 4) 2025, 5) 10 000, 6) 145 161.
Найти куб чисел:
Ответ: 1) 8, 2) 216, 3) 1 331, 4) 46 656, 5) 474 552, 6) 1 520 875.
✍ 3адание 2
Решить выражения:
Ответ: 1) 726, 2) 3 079, 3) 3 921, 4) 568, 5) 738, 6) 1 217.
§ 3адания на тему «Обыкновенные дроби»
✍ 3адание 1
1. Паша собрал 34 гриба, из которых 16 грибов оказались подосиновиками. Какую часть от всех грибов составляют подосиновики?
Ответ: 8/17.
2. Всего в книге 124 страниц, из которых Толя прочитал ровно половину. Какую часть книги прочитал Толя?
Ответ: 1/2.
3. Оля собрала всего 38 ягод, из которых 17 штук были малиной. Какую часть от общего количества составляют остальные ягоды?
✍ 3адание 2
Начертите отрезок и разделите его на 13 равных частей. Отметьте на данном отрезке: 3/13, 6/13, 10/13.
✍ 3адание 3
1. Полина собрала 36 листьев, из которых березовые составляют 6/18. Сколько березовых листьев собрала Полина?
Ответ: 12.
2. Папа был на рыбалке и поймал всего 45 рыбок, 8/15 было карасей. Сколько карасей поймал папа?
Ответ: 24.
3. Мама стряпала пирожки, всего их получилось 32 штуки. 5/8 от общего количества были с капустой. Сколько пирожков с капустой состряпала мама?
Ответ: 20.
✍ 3адание 4
Сравнить дроби:
§ 3адания на тему «Сложение и вычитание обыкновенных дробей»
✍ 3адание 1
Ответ: 1) 19/30, 2) 7/19, 3) 1/50, 4) 51/76, 5) 2/43.
✍ 3адание 2
Расстояние от дома до школы составляет 4/11 км, а от школы до магазина — 5/11 км. Чему равно расстояние от дома до магазина?
Решение: Для того чтобы найти сколько составляет весь путь, необходимо сложить расстояние от дома до школы и расстояние от школы до магазина 4/11 + 5/11 = 9/11 (км).
Ответ: Расстояние от дома до магазина составляет 9/11 км.
✍ 3адание 3
От рулона ткани первый раз отрезали 7/15 части, а затем еще 5/15, после чего в рулоне осталось 27 м. Сколько метров длина рулона?
Решение: В первую очередь нужно узнать какая часть рулона осталась.
1 действие: 15/15 — 7/15 — 5/15 = 3/15.
Можно сделать вывод, что 27 м составляет 3/15 части от всего рулона. Для того чтобы найти длину всего рулона ткани, необходимо узнать, сколько метров составляет 7/15 и 5/15 частей.
2 действие: 27 : 3 = 9 (м) — в 1 части.
3 действие: 9 • 7 = 63 (м) — составляет 7/15.
4 действие: 9 • 5 = 45 (м) — составляет 5/15.
После того, как стало известно какая длина у каждой из частей, можно вычислить всю длину рулона.
5 действие: 63 + 45 + 27 = 135 (м).
Ответ: длина рулона 135 метров.
§ 3адания на тему «Умножение и деление обыкновенных дробей»
✍ 3адание 1
Ответ: 1) 4/13, 2) 1/3, 3) 2/9, 4) 21/16, 5) 36/55.
✍ 3адание 2
В первом ящике лежит 3/16 от всего количества яблок, а во втором в 3 раза больше. Какая часть от всего количества яблок лежит в обоих ящиках?
Решение: Сначала нужно узнать сколько яблок лежит во втором ящике.
1 действие: 3/16 •3 = 9/16 (яб.).
После того как стало известно сколько яблок лежит во втором ящике, можно узнать их общее количество.
2 действие: 3/16 + 9/16 = 12/16 = 3/4 (яб.)
Ответ: 3/4 части от общего количества яблок лежит в обоих ящиках.
✍ 3адание 3
3а два дня автомобиль поехал 6/10 пути. Известно, что во второй день он проделал путь в 4 раза больше, чем в первый. Cколько проехал автомобиль в первый и второй день?
Решение: Пусть первый день пути будет x, тогда можно составить уравнение x + х • 4 = 6/10.
х + х • 4 = 6/10;
5 • x = 6/10;
х = 6/10 : 5;
х = 3/25 — проехал автомобиль в 1 день.
После того как стало известно, какая часть пути была преодолена в 1 день, можно высчитать 2 день.
2 действие: 3/25 • 4 = 12/25.
Ответ: в первый день автомобиль проехал 3/25, а во второй — 12/25.
§ 3адания на тему «Десятичные дроби»
✍ 3адание 1
Представить обыкновенные дроби в виде десятичных:
Ответ: 1) 0,5; 2) 0,13; 3) 0,2; 4) 0,164; 5) 0,18.
✍ 3адание 2
Начертите отрезок, разделите его на 6 равных частей. Отметьте на нем точки 0,3; 1,5; 2,2; 3,7; 4; 5,6.
§ 3адания на тему «Сложение и вычитание десятичных дробей»
✍ 3адание 1
Ответ: 1) 32,75; 2) 77; 3) 7,28; 4) 31,9; 5) 18,7; 6) 8,933.
✍ 3адание 2
В первый день катер проплыл 3,5 км, во второй на 4,31 км больше, а в третий — на 0,9 км меньше, чем во второй. Сколько всего км проплыл катер за 3 дня?
Решение: Необходимо вычислить, сколько катер проплыл в первый и во второй день.
1 действие: 3,5 + 4,31 = 7,81 (км) — проплыл во второй день.
2 действие: 7,81 — 0,9 = 6,91 (км) — проплыл в третий день.
После того как стало известно, сколько было пройдено за каждый день, можно узнать весь путь.
3 действие: 3,5 + 7,81 + 6,91 = 18,22 (км).
Ответ: за три дня катер проплыл 18,22 км.
§ 3адания на тему «Умножение и деление десятичных дробей»
✍ 3адание 1
Ответ: 1) 46,704; 2) 274,512; 3) 19,544; 4) 2,125; 5) 2,7; 6) 9,54.
✍ 3адание 2
3агадано число, если его увеличить в 3 раза, а затем прибавить 2,16, то получиться 27,96. Какое число было загадано?
Решение: Пусть неизвестное число будет x, тогда можно составить уравнение х • 3 + 2,16 = 27,96.
Ответ: было загадано число 8,6.
✍ 3адание 3
Расстояние между населенными пунктами равно 53,7 км. Навстречу друг другу вышли два пешехода, скорость первого 3,8 км/ч, второго — 4,6 км/ч. Какое расстояние будет между ними через 2,7 часа?
Решение: Нужно вычислить, какое расстояние пешеходы пройдут за 2,7 часа.
1 действие: 3,8 • 2,7 = 10,26 (км) — пройдет первый пешеход.
2 действие: 4,6 • 2,7 = 12,42 (км) — пройдет второй пешеход.
После того как стало известно, сколько прошли пешеходы, можно высчитать, какой путь им еще нужно преодолеть до встречи друг с другом.
3 действие: 53,5 — 10,26 — 12,42 = 30,82 (км).
Ответ: через 2,7 часа между пешеходами будет 30,82 км.
Контрольная работа по математике для 5 класса, 4 четверть. Проценты. Среднее арифметическое.
Вариант 1.
1. Выполните задания:
Выразите в виде десятичной дроби 3%. Запишите в процентах число 1,1.
2. Выполните задание:
Запишите среднее арифметическое чисел: 3, 4,5, 12.
3. Вычислите:
4. Решите задачу:
Велосипедист ехал со скоростью 18 км/час в течении 2,1 часа, а со скоростью 22 км/час 1,9 часа. Вычислите среднюю скорость велосипедиста.
5. Решите задачу:
В овощном магазине за 3 дня было продано 680 кг картофеля. В первый день продали 28% всего картофеля, во второй 25% от остатка. Сколько кг картофеля было продано в третий день?
6. Решите задачу:
Группа туристов путешествовала 3 дня. В первый день они преодолели 30% всего пути, во второй 22%, а в третий остальные 24 км. Какое расстояние преодолели туристы за 3 дня?
7. Дополнительное задание:
Среднее арифметическое четырех чисел равно 2,765, а среднее арифметическое других трех чисел равно 3,01. Вычислите среднее арифметическое этих семи чисел.
Вариант 2.
1. Выполните задания:
Выразите в виде десятичной дроби 9%. Запишите в процентах число 2,7.
2. Выполните задание:
Запишите среднее арифметическое чисел 3,2, 4, 17,4.
3. Вычислите:
4. Решите задачу:
Грузовой автомобиль 2,4 часа ехал со скоростью 59,4 км/час и 3,6 часа со скоростью 44,8 км/час. Вычислите среднюю скорость грузового автомобиля за все время пути.
5. Решите задачу:
Три грузчика за смену выгрузили 40 тонны цемента. Один выгрузил 30% всего цемента, второй 48% от остатка. Сколько тонн цемента выгрузил третий грузчик?
6. Решите задачу:
В торговый павильон завезли абрикосы, груши и яблоки. Абрикосы составляли 27% всех фруктов, яблоки 31%, а груши остальные 42,21 кг. Сколько всего фруктов завезли в торговый павильон?
7. Дополнительное задание:
Среднее арифметическое некоторых 3 чисел равно 3,7, а некоторых других, пяти чисел 2,9. Вычислите среднее арифметическое этих восьми чисел.