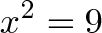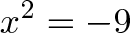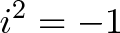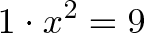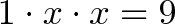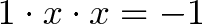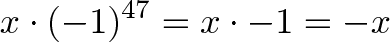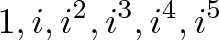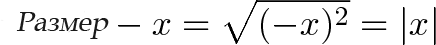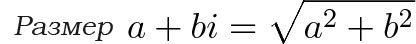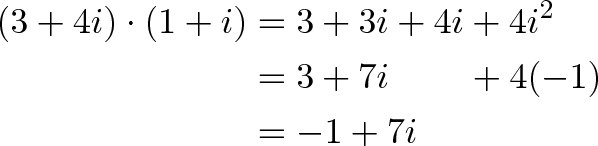зачем нужны комплексные числа кратко

Откуда есть пошло комплексное число

В современной математике комплексное число является одним из фундаментальнейших понятий, находящее применение и в «чистой науке», и в прикладных областях. Понятно, что так было далеко не всегда. В далекие времена, когда даже обычные отрицательные числа казались странным и сомнительным нововведением, необходимость расширения на них операции извлечения квадратного корня была вовсе неочевидной. Тем не менее, в середине XVI века математик Рафаэль Бомбелли вводит комплексные (в данном случае точнее сказать, мнимые) числа в оборот. Собственно, предлагаю посмотреть, в чем была суть затруднений, доведших в итоге солидного итальянца до подобных крайностей.

Существует распространенное заблуждение, что комплексные числа потребовались для того, чтобы решать квадратные уравнения. На самом деле, это совершенно не так: задача поиска корней квадратного уравнения никоим образом введение комплексных чисел не мотивирует. Вот совершенно.

Давайте убедимся сами. Всякое квадратное уравнение можно представить в виде:
.
Геометрически, это означает, что мы хотим найти точки пресечения некоторой прямой и параболы
Я тут даже картинку сделал, для иллюстрации.

Как нам всем хорошо известно из школы, корни квадратного уравнения (в указанных выше обозначениях) находятся по следующей формуле:

Оказываются возможными 3 варианта:
1. Подкоренное выражение положительно.
2. Подкоренное выражение равно нулю.
3. Подкоренное выражение отрицательно.

В первом случае имеются 2 различных корня, во втором два совпадающих, в третьем уравнение «не решается». Все эти случаи имеют вполне наглядную геометрическую интерпретацию:
1. Прямая пересекает параболу (синяя прямая на рисунке).
2. Прямая касается параболы.
3. Прямая не имеет с параболой общих точек (сиреневая прямая на рисунке).

Ситуация проста, логична, непротиворечива. Пытаться извлекать квадратный корень из отрицательного числа нет совершенно никаких оснований. Никто и не пытался.

Обстановка существенно изменилась, когда пытливая математическая мысль добралась до кубических уравнений. Чуть менее очевидно, используя некоторую несложную подстановку, всякое кубическое уравнение можно свести к виду: . С геометрической точки зрения ситуация похожа на предыдущую: мы ищем точку пересечения прямой и кубической параболы.
Взгляните на картинку:

Существенное отличие от случая квадратного уравнения в том, что какую бы прямую мы не взяли, она всегда пересечет параболу. Т.е., уже из чисто геометрических соображений, кубическое уравнение всегда имеет хотя бы одно решение.
Найти его можно воспользовавшись формулой Кардано:

где
.
Немного громоздко, но пока, вроде бы, все в порядке. Или нет?

Вообще, формула Кардано — это яркий пример «принципа Арнольда» в действии. И что характерно, Кардано никогда на авторство формулы не претендовал.

Вернемся, однако, к нашим баранам. Формула замечательная, без преувеличение великое достижение математики начала-середины XVI века. Но есть у нее один нюанс.
Возьмем классический пример, который рассматривал еще Бомбелли:
.
Внезапно,
,
и, соответственно,
.
Приплыли. А формулу жалко, а формула-то хорошая. Тупик. При том, что решение у уравнения, безусловно, есть.

Идея Рафаэля Бомбелли заключалась в следующем: давайте прикинемся шлангом и сделаем вид, что корень из отрицательного — это какое-то число. Мы, конечно, знаем, что таких чисел нет, но тем не менее, давайте представим, что оно существует и его, как обычные числа, можно складывать с другими, умножать, возводить в степень и т.п.

Используя подобный подход, Бомбелли установил, в частности, что
,
и
.
Давайте проверим:
.
Заметьте, в выкладках никаких предположений о свойствах квадратных корней из отрицательных чисел не предполагалось, кроме упомянутого выше допущения, что они ведут себя как «обычные» числа.

В сумме получаем . Что вполне себе правильный ответ, который элементарно проверяется прямой подстановкой. Это был настоящий прорыв. Прорыв в комплексную плоскость.

Тем не менее, подобные выкладки выглядят как некоторая магия, математический фокус. Отношение к ним, как к некоему трюку, сохранялось среди математиков еще очень долго. Собственно, придуманное Рене Декартом для корней из отрицательных название «мнимые числа» вполне отражает отношение математиков тех времен к таким развлечениям.

Однако, время шло, «трюк» применялся с неизменным успехом, авторитет «мнимых чисел» в глазах математического общества рос, сдерживаемый, однако, неудобством их использования. Лишь получение Леонардом Эйлером (кстати, это именно он ввел ныне общеупотребительное обозначение для мнимой единицы) знаменитой формулы

открыло комплексным числам дорогу в самые различные области математики и ее приложений. Но это уже совсем другая история.

Источник

Введение в комлексные числа

Выяснив, что многие знакомые программисты не помнят комплексные числа или помнят их очень плохо, я решил сделать небольшую шпаргалку по формулам.

А школьники могут что-то новое узнать 😉
// Всех кого заинтересовал прошу под кат.

Итак, комплексные числа эта такие числа, которые можно записать как

Где x, y вещественные числа(т.е привычные всем числа), а i — число, для которого
выполняется равенство

x называется действительной частью, y — мнимой.

Это алгебраическая форма записи комплексного числа.

Существует также тригонометрическая форма записи комплексного числа z:

С введением, пожалуй, все.

Переходим к самому интересному — операциям над комплексными числами!
Для начала рассмотрим сложение.

У нас есть два таких комплексных числа:

Как же их сложить?
Очень просто: сложить действительную и мнимую части.
Получим число:

Все просто, не так ли?
Вычитание выполняется аналогично сложению.
Нужно просто вычесть из действительной части 1 числа действительную часть 2 числа,
а потом проделать тоже с мнимой частью.
Получим число

Умножение выполняется вот так:

Напомню, x это действительная часть, y — мнимая.
Деление выполняется вот так:

Кстати, поддержка комплексных чисел есть в стандартной библиотеке Python:

Вместо i используется j.
Кстати, это потому что Python принял конвенцию инженеров-электриков, у которых
буква i обозначает электрический ток.
Задавайте свой вопросы, если они есть, в комментариях.
Надеюсь, вы узнали для себя что-то новое.

UPD: В комментариях просили рассказать о практическом применении.
Так вот комплексные числа нашли широкое практическое применение в авиации
(подъемная сила крыла) и в электричестве.
Как видете, очень нужная вещь 😉

Источник

Статья на тему «Комплексные числа»

Ищем педагогов в команду «Инфоурок»

1.Для чего нужны комплексные числа?

В любой науке любая математика должна по идее быть математикой комплексных чисел. Дело в том, что из всех наук, только физика наиболее математизирована. И математические методы наиболее сильно проникли в физику. Комплексные числа также используются в исследовании течения воды, вычерчивании географических карт, конструривании ракет и самолетов.

Комплексные числа, как и отрицательные, возникли из внутренней потребности самой математики – из практики и теории решения алгебраических уравнений. С комплексными числами впервые математики встретились при решении квадратных уравнений. До 16 века математики всего мира, не находя приемлемого толкования для комплексных корней, возникавших при решении квадратных уравнений, объявляли их ложными и не принимали во внимание. Только в начале 19 века, когда уже была выяснена роль комплексных чисел в различных областях математики, была разработана очень простая и естественная их геометрическая интерпретация, позволившая уяснить геометрический смысл операций над комплексными числами. Тем самым был положен конец сомнениям в законном и полезном применении комплексного числа.

2.Действия над комплексными числами в алгебраической форме.

Над комплексными числами в алгебраической форме можно выполнять следующие действия.

Умножение комплексных чисел обладает следующими свойствами:

3º. Дистрибутивность умножения относительно сложения:

На практике умножение комплексных чисел производят по правилу умножения суммы на сумму и выделения действительной и мнимой части.

В следующем примере рассмотрим умножение комплексных чисел двумя способами: по правилу и умножением суммы на сумму.

На практике частное комплексных чисел находят путем умножения числителя и знаменателя на число, сопряженное знаменателю.

В следующем примере выполним деление по формуле и правилу умножения на число, сопряженное знаменателю.

Поэтому, чтобы возвести число i в целую положительную степень, надо показатель степени разделить на 4 и возвести i в степень, показатель которой равен остатку от деления.

3.Извлечение корней из комплексных чисел.

Вычислить

Можно извлечь два корня:

Что и требовалось проверить.

4.Тригонометрическая форма комплексного числа

Модулем комплексного числа называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длина радиус-вектора, который на чертеже обозначен красным цветом.

Модуль комплексного числа обозначают или

По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: . Данная формула справедлива для любых значений « а » и « b ».

Аргументом комплексного числа называется угол между положительной полуосью действительной оси и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа: .

. Для нахождения аргумента получается следующая формула:
.

Данная формула работает только в правой полуплоскости! Если комплексное число располагается не в 1-й и не 4-й координатной четверти, то формула будет немного другой.

Источник

Что такое комплексные числа

Содержание статьи

Общее понятие о комплексном числе

Если вам нужно назвать расстояние между двумя городами, то можно дать ответ, состоящий из одного числа в милях, километрах или в других единицах измерения линейных расстояний. Однако если вы должны описать, как добраться из одного города в другой, то необходимо дать больше информации, чем просто расстояние между двумя точками на карте. В этом случае стоит сказать о направлении, в котором надо двигаться и о времени движения.

Вид информации, которая выражает одномерное измерение, в науке называется скалярной величиной. Скаляры – это числа, используемые в большинстве математических расчетов. К примеру, масса и скорость, которыми обладает тот или иной объект являются скалярными величинами.

Для того чтобы успешно анализировать природные явления, мы должны работать с абстрактными объектами и методами, способными представлять многомерные величины. Здесь необходимо отказываться от скалярных чисел в пользу комплексных. Они дают возможность выразить два измерения одновременно.

Комплексные числа легче понять, когда они представлены в графическом виде. Если нарисовать линию, имеющую определенную длину и направление, то это и будет графическое представление комплексного числа. Оно также широко известно в физике как вектор.

Различия между комплексными и скалярными величинами

Такие типы чисел, как целые, рациональные, иррациональные и реальные знакомы детям со школы. Им всем присуща одномерность. Прямолинейность числовой прямой иллюстрирует это графически. Вы можете перемещаться вверх или вниз по ней, но все «движения» по этой линии будут ограничиваются горизонтальной осью. Одномерных, скалярных цифр вполне достаточно для подсчета количества предметов, выражения веса или измерения постоянного напряжения батареи. Но они не могут обозначать что-то более сложное. Скалярами невозможно одновременно выразить расстояние и направление между двумя городами, или амплитуду с фазой. Представлять эти виды чисел необходимо уже в виде многомерной области значений. Другими словами, нам нужны векторные величины, которые могут иметь не только величину, но и направление распространения.

Заключение

Вектор является графическим изображением комплексного числа. Он выглядит, как стрелка с начальной точкой, определенной длиной и направлением. Иногда слово «вектор» используется в радиотехнике, где он выражает фазовый сдвиг между сигналами.

Источник

Просто о сложном: комплексные числа

Комплексные числа всегда меня занимали. Как и с понятием экспоненты, большинство определений подпадали под одну из двух категорий:

Какой хороший способ привлечь деток к математике! Сегодня мы возьмем эту тему штурмом, используя наши любимые инструменты:

И наше секретное оружие: изучение по аналогии. Мы доберемся до комплексных чисел, начав с их предков, отрицательных чисел. Вот вам небольшое руководство:

Пока что смысла в этой таблице мало, но пусть она будет рядом. К концу статьи всё станет на свои места.

Давайте действительно поймем, что такое отрицательные числа

Отрицательные числа не так просты. Представьте, что вы — европейский математик в XVIII веке. У вас есть 3 и 4, и вы можете написать 4 – 3 = 1. Всё просто.

Но сколько будет 3 – 4? Что, собственно, это означает? Как можно отнять 4 коровы от 3? Как можно иметь меньше, чем ничего?

Отрицательные числа рассматривались как полная чушь, что-то, что «бросало тень на всю теорию уравнений» (Фрэнсис Масерес, 1759). Сегодня было бы полной чушью думать об отрицательных числах, как о чем-то нелогичном и неполезном. Спросите вашего учителя, нарушают ли отрицательные числа основы математики.

Что же произошло? Мы изобрели теоретическое число, которое обладало полезными свойствами. Отрицательные числа нельзя потрогать или ощутить, но они хорошо описывают определенные связи (как задолженность, например). Это очень полезная выдумка.

Вместо того, чтобы сказать «Я должен вам 30», и читать слова, чтобы понять в плюсе я или в минусе, я могу просто записать «-30», и знать, что это означает. Если я заработаю деньги и оплачу свои долги (-30 + 100 = 70), я смогу легко записать эту транзакцию несколькими символами. У меня останется +70.

Знаки плюса и минуса автоматически фиксируют направление — вам не нужно целое предложение, чтобы описать изменения после каждой транзакции. Математика стала проще, элегантнее. Стало не важно, являются ли отрицательные числа «осязаемыми» — у них есть полезные свойства, и мы пользовались ими, пока они крепко не вошли в наш обиход. Если кто-то из ваших знакомых еще не понял суть отрицательных чисел, теперь вы ему поможете.

Но не будем умалять человеческие страдания: отрицательные числа были настоящим сдвигом в сознании. Даже Эйлер, гений, открывший число е и много еще чего, не понимал отрицательные числа так же хорошо, как мы сегодня. Они рассматривались как «бессмысленные» результаты вычислений.

Странно требовать от детей, чтобы они спокойно понимали идеи, которые когда-то смущали даже самых лучших математиков.

Ввод мнимых чисел

С мнимыми числами та же история. Мы можем решать уравнения вроде этого целыми днями:

Ну и ну. Такой вопрос заставляет людей съеживаться, первый раз видя его. Вы хотите вычислить квадратный корень из числа, меньшего, чем ноль? Это немыслимо! (Исторически реально существовали подобные вопросы, но мне удобнее представлять какого-то безликого умника, чтобы не вгонять в краску ученых прошлого).

Выглядит безумно, как в свое время выглядели и отрицательные числа, ноль и иррациональные числа (неповторяющиеся числа). В этом вопросе нет «реального» смысла, правда?

Ну, сначала у нас конечно болит голова. Но, играя в игру «Давайте представим, что i существует», мы действительно делаем математику проще и элегантнее. Появляются новые связи, которые мы с легкостью можем описать.

Я не люблю сам термин «мнимые числа» — такое чувство, что он был выбран специально, чтобы оскорбить чувства i. Число i такое же нормальное, как и другие, но за ним закрепилась кличка «мнимое», так что мы тоже будем ей пользоваться.

Визуальное понимание отрицательных и комплексных чисел

Уравнение x^2 = 9 на самом деле означает следующее:

Какое преобразование x, применяемое дважды, превращает 1 в 9?

Это довольно круто! У нас есть что-то вроде решения, но что оно означает?

Все числа 2-мерные. Да, это трудно принять, но древним римлянам было бы также трудно принять десятичные дроби или деление в столбик. (Как это так, между 1 и 2 есть еще числа?). Выглядит странно, как и любой новый способ мыслить в математике.

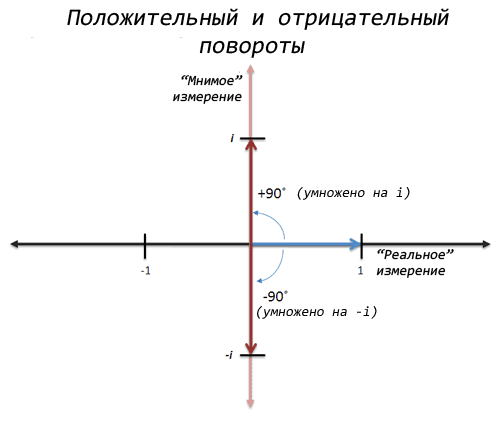
Также, не забывайте, что принятие оборота против часовой стрелки за положительный результат — это сугубо человеческая условность, и всё могло бы быть совсем по-другому.

Поиск множеств

Это очень полезная мысль. Число «х» может представлять хорошие и плохие недели. Представим, что хорошая неделя сменяет плохую; это хорошая неделя; а какой будет 47-я неделя?

-x означает, что неделя выдастся плохой. Видите, как отрицательные числа «следят за знаком» — мы можем просто ввести (-1)^47 в калькуляторе вместо того, чтобы считать («Неделя 1 хорошая, неделя 2 плохая… неделя 3 хорошая…»). Вещи, которые постоянно чередуются можно отлично смоделировать, используя отрицательные числа.

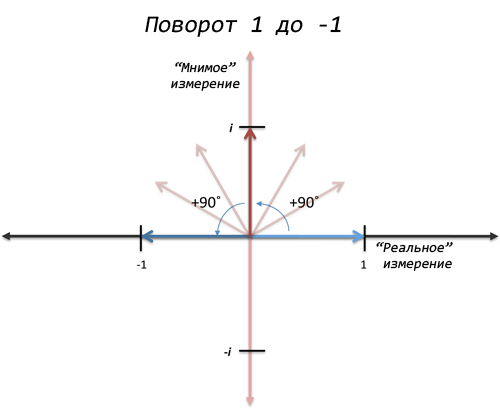
Хорошо, а что будет, если мы продолжим умножать на i?

Очень смешно, давайте немного это всё упростим:

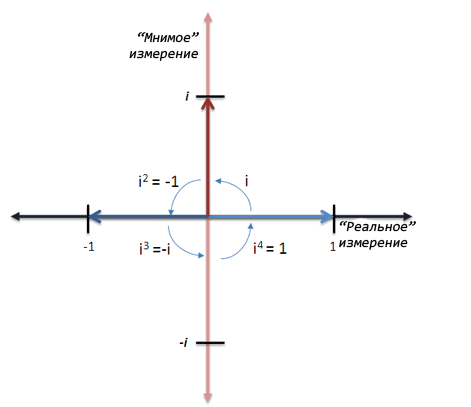
Вот всё то же представлено графически:

Мы повторяем цикл каждый 4-й поворот. В этом определенно есть смысл, да? Любой ребенок скажет вам, что 4 поворота влево — это всё равно, что не поворачиваться вовсе. А теперь оторвитесь от мнимых чисел (i, i^2)и посмотрите на общее множество:

Точно, как отрицательные числа моделируют зеркальное отражение чисел, мнимые числа могут моделировать что угодно, что вращается между двумя измерениями «Х» и «Y». Или что угодно с циклической, круговой зависимостью — есть что-нибудь на примете?

Понимание комплексных чисел

Есть еще одна деталь для рассмотрения: может ли число быть и «реальным», и «мнимым»?

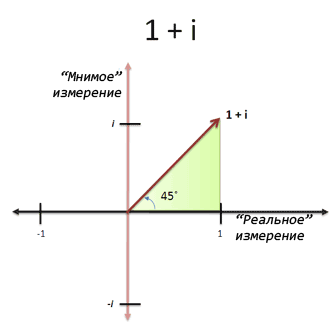
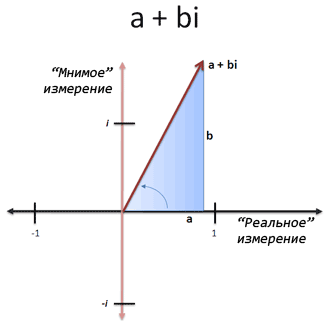
Даже не сомневайтесь. Кто сказал, что нам обязательно нужно поворачивать строго на 90 градусов? Если мы одной ногой станем на «реальную» размерность, а другой — на «мнимую», то будет выглядеть примерно так:

Мы находимся на отметке в 45 градусов, где вещественная и мнимая части одинаковы, и само число равно «1 + i». Это как хот-дог, где есть и кетчуп, и горчица — кто сказал, что нужно обязательно выбирать что-то одно?

По сути, мы можем выбрать любую комбинацию вещественной и мнимой части и сделать из всего этого треугольник. Угол становится «углом вращения». Комплексное число — это заумное название для чисел, в которых есть вещественная и мнимая части. Они пишутся, как «a + bi», где:

Неплохо. Но остается один последний вопрос: как «велико» комплексное число? Мы не можем измерить вещественную часть или мнимую отдельно, потому что мы упустим общую картину.

Давайте сделаем шаг назад. Размер отрицательного числа — это расстояние от нуля:

Это другой способ найти абсолютную величину. Но как измерить оба компонента на 90 градусах для комплексных чисел?

Это птица в небе… или самолет… Пифагор спешит на помощь!

Эта теорема выскакивает, где только можно, даже в числах, придуманных через 2000 лет после самой теоремы. Да, мы делаем треугольник, и его гипотенуза и будет равна расстоянию от нуля:

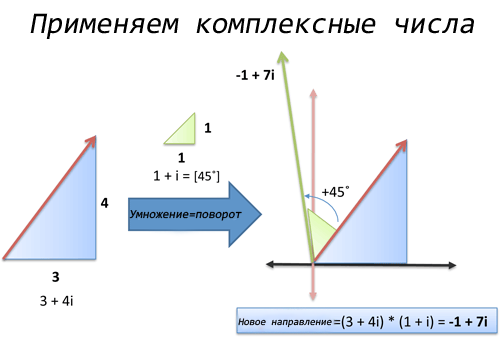
Реальный пример: Вращения

Мы не будем дожидаться университетского курса физики, чтобы попрактиковаться с комплексными числами. Мы займемся этим уже сегодня. Много можно рассказать на тему умножения комплексных чисел, но пока нужно понять главное:

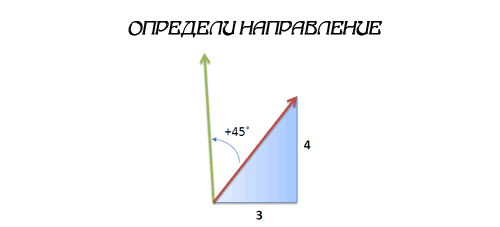
Давайте посмотрим, как это работает. Представьте, что я на лодке, движусь с курсом 3 единицы на Восток каждые 4 единицы на Север. Я хочу изменить свой курс на 45 градусов против часовой стрелки. Каким будет мой новый курс?

Кто-то может сказать «Это просто! Вычислите синус, косинус, погуглите значение по тангенсу…и тогда…» Кажется, я сломал свой калькулятор…

Давайте пойдем более простым путем: мы идем по курсу 3 + 4i (не важно, какой тут угол, нам всё равно пока) и хотим повернуться на 45 градусов. Ну, 45 градусов это 1 + i (идеальная диагональ). Так что мы можем умножить наш курс на это число!

При умножении мы получаем:

Наш новый ориентир — 1 единица на Запад (-1 на Восток) и 7 единиц на Север, можете нарисовать координаты на графике и следовать им.

Но! Мы нашли ответ за 10 секунд, без всяких синусов и косинусов. Не было векторов, матриц, отслеживания, в каком квадранте мы находимся. Это была простая арифметика и немного алгебры для приведения уравнения. Мнимые числа отлично справляются с вращением!

Более того, результат такого вычисления очень полезен. У нас есть курс (-1, 7) вместо угла (atan(7/-1) = 98.13, и сразу ясно, что мы во втором квадранте. Как, собственно, вы планировали нарисовать и следовать указанному углу? Используя транспортир под рукой?

Нет, вы бы конвертировали угол в косинус и синус (-0.14 и 0.99), нашли бы примерное соотношение между ними (около 1 к 7) и набросали бы треугольник. И тут комплексные числа несомненно выигрывают — аккуратно, молниеносно, и без калькулятора!

Если вы похожи на меня, то это открытие покажется вам сногсшибательным. Если нет, боюсь, что математика вас совсем не зажигает. Уж извините!

Тригонометрия хороша, но комплексные числа значительно упрощают вычисления (вроде поиска cos(a + b)). Это только маленький анонс; в следующих статьях я предоставлю вам полное меню.

Лирическое отступление: некоторые люди думают примерно так: «Эй, ну не удобно же иметь курс Север/Восток вместо простого угла для следования судна!»

Правда? Ну хорошо, посмотрите на свою правую руку. Какой угол между основанием вашего мизинца и кончиком указательного пальца? Удачи с вашим способом вычисления.

А можно просто ответить «Ну, кончик находится на Х дюймов вправо и Y дюймов вверх» и с этим уже можно что-то сделать.

Комплексные числа стали ближе?

Мы пронеслись смерчем по моим базовым открытиям в области комплексных чисел. Посмотрите на самую первую иллюстрацию, теперь он должен стать более понятным.

Есть еще столько всего интересного в этих красивых, чудных числах, но мой мозг уже устал. Моя цель была проста:

Если я кажусь слишком озабоченным этой темой, то для этого есть причина. Мнимые числа годами были моей навязчивой идеей — недостаток понимания меня раздражал.

Сейчас я наконец-то дошел до этого долгожданного понимания, и мне не терпелось поделиться с вами. Но меня по-прежнему злит, что вы знакомитесь с этими замечательными, несложными приемами понимания в блоге какого-то безумного лунатика, а не в классе на уроке математики. Мы душим в себе вопросы и «пыхтим» над непонятными вещами, потому что не хотим искать, находить и делиться чистыми, абсолютно логичными объяснениями.

Но зажечь свечу лучше, чем пробираться сквозь кромешную тьму: вот мои мысли, и я уверен, что огонек зажжется и в умах моих читателей.

Эпилог: Но они по-прежнему довольно странные!

Я знаю, они и для меня всё еще выглядят странными. Я пытаюсь мыслить, как мыслил первый человек, открывший ноль.

Ноль — это такая странная идея, «что-то» представляет «ничего», и это никак не могли понять в Древнем Риме. То же самое и с комплексными числами — это новый способ мышления. Но и ноль, и комплексные числа значительно упрощают математику. Если бы мы никогда не внедряли странности вроде новых систем счисления, мы бы до сих пор считали всё на пальцах.

Я повторяю эту аналогию, потому что так легко начать думать, что комплексные числа «не нормальные». Давайте быть открытыми к новшествам: в будущем люди будут только шутить над тем, как кто-то вплоть до XXI века не верил в комплексные числа.

Источник