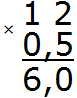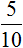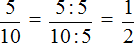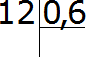зачем нужны десятичные дроби
Исследования учащихся по теме Кому и зачем нужны десятичные числа
Содержание
Тема исследования
Какие действия можно производить с десятичными дробями
Актуальность проблемы
Расширение понятия числа и появление новых видов связей между числами, всевозможных способов выполнения различных действий с данными числами.
Выяснить какие действия можно производить с десятичными дробями, кому и зачем они нужны, и можно ли стать успешным в жизни, не зная теории чисел.
Задачи
Рассмотреть десятичные дроби со следующих точек зрения:
Гипотеза
Предполагаем, что в жизни мы можем обойтись без десятичных дробей, используя другие числа.
Этапы исследования
1. Определение проблемы и вытекающих из нее задач исследования.
2. Выдвижение гипотезы их решения.
3. Обсуждение методов исследования.
4. Поиск теоретической информации.
5. Подбор примеров к каждому разделу теории.
6. Оформление результатов поиска в виде презентации.
7. Подведение итогов.
Объект исследования
Методы
1. Эмпирические: наблюдение и опрос(анкетирование учащихся,сбор информации по различным источникам)
2. Теоретические: анализ и синтез( анализ промежуточных исследований)
Ход работы
1. Поиск различных источников информации по теме.
2. Анализ найденной информации и составление конспекта по теме.
3. Создание дидактических материалов по теме.
4. Представление результата в виде презентации.
Наши результаты
1.Защита исследовательской работы на уроке.
2.Отчетная презентация по исследовательской работе.
3.Тематическая газета к предметной неделе в школе.
Выводы
Список ресурсов
Применение десятичных дробей
Десятичные дроби имеют широкий спектр применения. Их применяют в экономике, медицине, машиностроении и во многих других отраслях. В данном уроке мы рассмотрим некоторые элементарные операции, которые могут пригодиться в будущем.
Сравнение десятичных дробей
Чтобы сравнить две десятичные дроби, нужно в обеих дробях сделать количество цифр после запятой одинаковым, приписáв к одной из них нули. Затем отбросить запятые в обеих дробях и сравнить получившиеся числа.
Значит и дробь 5,345 меньше, чем дробь 5,36
Пример 2. Сравнить десятичные дроби 6,782 и 6,71
Сделаем количество цифр в обеих дробях одинаковым:
6782 больше, чем 6710
Значит и дробь 6,782 больше, чем дробь 6,71
Нахождение десятичной дроби от числа
В прошлых уроках мы находили обыкновенную дробь от числа. Для этого мы делили число на знаменатель дроби и полученный результат умножáли на числитель дроби.
Например, чтобы найти от числа 9, нужно число 9 разделить на знаменатель дроби и полученный результат умножить на числитель этой же дроби
Значит от числа 9 составляет 6.
Но находить можно и десятичные дроби от числа. Нахождение десятичной дроби от числа намного проще. Чтобы найти десятичную дробь от числа, достаточно это число умножить на данную дробь.
Например, найдём 0,5 от числа 12. Чтобы найти 0,5 от числа 12, достаточно умножить 12 на 0,5
Получили ответ 6. Значит 0,5 от числа 12 составляет число 6.
Проверим правильно ли мы нашли 0,5 от числа 12. Сначала переведём десятичную дробь 0,5 в обыкновенную дробь. 0,5 это ноль целых и пять десятых. Ноль не пишем, а записываем сразу пять десятых:
Cделаем эту дробь более простой для нашей работы. Для этого сократим её на 5
Получили дробь 


Пример 2. Найти 0,4 от одного метра
Один метр это 100 см. Чтобы найти 0,4 от 100 см, нужно 100 см умножить на 0,4. А чтобы умножить 100 см на 0,4 нужно в 0,4 перенести запятую вправо на две цифры:
Значит 0,4 от одного метра составляют 40 см.
Десятичную дробь также можно найти от десятичной дроби. Например, найдем 0,5 от 2,5. Для этого 2,5 нужно умножить на 0,5
Нахождение числа по десятичной дроби
В прошлых уроках мы находили число по обыкновенной дроби. Чтобы найти всё число по его дроби мы делили известное число на числитель дроби и полученный результат умножали на знаменатель дроби.
Например, если 
Значит если всё число равно 12.
Находить число можно и по десятичной дроби. Нахождение числа по десятичной дроби намного проще. Чтобы найти число по десятичной дроби, достаточно это число разделить на данную дробь.
Пример 1. 0,6 всего числа составляет 12, найти всё число. Чтобы найти всё число, достаточно 12 разделить на 0,6.
Чтобы разделить 12 на 0,6 нужно в делимом и в делителе перенести запятую вправо на одну цифру. Тогда получим выражение 120 : 6. А это выражение вычисляется легко:
Значит, если 0,6 всего числа составляет 12, то всё число это 20.
Пример 2. Велосипедист проехал 3 км, что составляет 0,2 всего пути, который должен проехать велосипедист. Какой путь должен проехать велосипедист?
Если 0,2 всего пути составляют 3 км, то для того чтобы найти весь путь, нужно 3 разделить на 0,2. Чтобы разделить число 3 на 0,2 нужно в делимом и в делителе перенести запятую вправо на одну цифру. Тогда получим выражение 30 : 2. А это выражение вычисляется легко:
Значит весь путь, который должен проехать велосипедист составляет 15 км.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
19 thoughts on “Применение десятичных дробей”
Спасибо владельцам ресурса за их труды! У меня проблемы с математикой) искал где учить, что бы было коротко и по делу и вот нашел ваш сайт. Радует чистый дизайн, который не отвлекает и типографика отличная
Огромное спасибо обладателю этого ресурса. Прекрасные уроки!
Было бы хорошо, если важные моменты выделяли в специальное обведенное поле, как правило, теорема или просто подсказка. Иногда читать одно и тоже по нескольку раз за статью очень отвлекает и начинаешь путаться, так как думаешь, что это разные правила
Здравствуйте. Спасибо за разумную критику. Уже думали над этим и хотим отказаться от такого формата. Причина по которой правило повторяется по нескольку раз за урок — чтобы человек понял, как его применять на практике. С первого раза мало кому удается «въехать».
помогите я запуталась. Сначало написано, что находя число от дроби, нужно умножить разделить на знаменатель, затем умножить на числитель, потом наоборот. Или я не понимаю.
Если находите обыкновенную дробь от числа, то делите число на знаменатель дроби и полученный результат умножаете на числитель.
Если находите десятичную дробь от числа, то просто умножаете это число на десятичную дробь.
Не меняйте ничего. Повторение очень помогает умвоению материала. Без этого вся информация улетучивпется очень быстро. Все идеально сделано. Это в первый раз когда я в е понимаю до мелочей и во ного благодаря повторению
Применение десятичной дроби в нашей жизни
Рассмотрим более подробно применение десятичных дробей в нашей жизни.
Дроби в медицине. В медицине, например, известно, что «великан» среди микробов имеет размер 0,1 мм, а наибольший мелкий вирус имеет размер 16 миллимикрон, т. е. (0,1: 1000 : 1000) х 16=0,0000016 (мм). Сравнивая размеры, медики определяют, чем вызвано заболевание (микробом или вирусом?), и узнают, какая болезнь». Дроби используются и в приготовление концентрированных растворов для жидких лекарств. Например, диагноз: закрытый перелом 1/3 (верхней) части голени. − Курс лечения: пить по 0,25 таблетки 3 раза в день, в течение 5 дней.
Дроби в кулинарии. В кулинарии (как и во всем поварском деле) все основывается на долях, на соотношениях. Стандартные рецепты приготовления видов хлеба (как пример) основываются на правилах долей.
В геодезии существует метод съемки земли, называемый космическое зондирование. Этот очень сложный метод можно упростить, используя дроби при расчетах формул. Благодаря им, геодезисты могут получить наиболее качественное изображение поверхности Земли. Дроби в космосе
Дроби в строительстве. Без знаний дробей невозможно построить здания, возвести мосты, проложить асфальт и т.д. Чтобы сделать строительный раствор необходимо знать дроби. Дроби используются в строительстве любого масштаба: для вычисления площадей и пропорций зданий, а также углов наклона стен и насыпей. Например, чтобы построить теплицу нужно измерить площадь земельного участка, толщину пленки. Оказывается, что и гвозди имеют размеры в десятичных дробях.
Дроби в рисовании. Для построения изображения головы человека высоту головы делим на 7 частей. Расстояние между глазами равно длине глаз. Ширина головы = 3\4 высоты головы
Дроби в фигурном катании. В фигурном катании десятичные дроби применяются при подсчете баллов для выявления победителей среди сильнейших фигуристов.
Дроби в музыке. В греческих сочинениях по математике дробей не встречалось. Греческие ученые считали, что математика должна заниматься только целыми числами. Возиться с дробями они предоставляли купцам, ремесленникам, а также астрономам, землемерам, механикам и другому «черному люду». Кроме арифметики и геометрии, в греческую науку входила музыка. Пифагорейцы, много занимавшихся музыкой и обожествлявшие число, считали, что Земля имеет форму шара и находится в центре Вселенной: ведь нет никаких оснований, чтобы она была смещена или вытянута в какую-то одну сторону. Солнце же, Луна и 5 планет (Меркурий, Венера, Марс, Юпитер и Сатурн) движутся вокруг Земли. Расстояния от них до нашей планеты таковы, что они как бы составляют семиструнную арфу, и при их движении возникает прекрасная музыка – музыка сфер. Обычно люди не слышат её из-за суеты жизни, и лишь после смерти некоторые из них смогут насладиться ею. А Пифагор слышал её при жизни. Его ученики – пифагорейцы, много занимавшиеся музыкой и обожествлявшие число, исследовали, насколько повышается тон струны, если её прижать посередине, или на четверть расстояния одного из концов, или на треть. Обнаружилось, что одновременное звучание двух струн приятно для слуха, если длины их относятся как 1:2, или 2:3, или 3:4, что соответствует музыкальным интервалам в октаву, квинту и кварту. Гармония оказалась тесно связанной с дробями, что подтверждало основную мысль пифагорейцев: «число правит миром»… Так дроби сыграли определяющую роль в музыке. И сейчас в общепринятой нотой записи длинная нота – целая – делится на половинки (вдвое короче), четверти, восьмые, шестнадцатые и тридцать вторые. Таким образом, ритмический рисунок любого музыкального произведения, созданного европейской культурой, каким бы сложным он ни был, определяется десятичными дробями.
Практическая часть
В качестве примера применения десятичных дробей в нашей жизни, я решил подготовить математическую игру для одноклассников. Я придумал несколько заданий. Которые можно использовать как на уроке, так и на внеклассном занятии. Данную игру я провел среди учащихся 5″а» класса, и вот какие отзывы я получил от них.
Афанасьев А.-Игра мне очень понравилась, заданий было много и все разнообразные.
Тарасов Е.- Игра была увлекательная и интересная.
Калинин Д.- Мне понравилась игра там было много интересных заданий.
Шамшина Д.- Игра помогла мне закрепить знания которые прошли на уроке.
Задачи
1.Сбербанк начисляет вкладчику 12 % годовых. Вкладчик положил на счет 30 000 руб. и не снимал деньги со счета в течение трех лет и не брал процентные начисления. Сколько денег будет на счете вкладчика через год? Через три года?
2.Холодильник стоил 12 600 руб. В мае цена холодильника была снижена на 20%, а в июне – еще на 5%. Какой стала стоимость холодильника в июне?
3.В начале года тариф на электроэнергию составлял 4,2 р. за 1кВт/ч. В середине года он увеличился на 10%, а в конце года еще на 4%. Каков тариф стал после повышения?4.Длина прямоугольного участка составляет 19,4 метра, а ширина на 2,8 метра меньше. Вычислите периметр участка.
5. В швейной мастерской было 5 цветов ленты. Красной ленты было больше, чем синей на 2,4 метра, но меньше, чем зеленой на 3,8 метра. Белой ленты было больше, чем черной на 1,5 метра, но меньше, чем зеленой на 1,9 метра. Сколько метров ленты всего было в мастерской, если белой было 7,3 метра?
Вопросы
Укажите верную запись десятичной дроби «три целых пять сотых»
Вопрос № 2
В каком разряде числа 6,0359 записана цифра 5?
сотых
тысячных
тысяч
десятых
Вопрос № 3
Запишите дробь 21,0100 короче.
Вопрос № 4
Между какими соседними натуральными числами находиться число 3,19?
3,1 и 3,2
3 и 19
3 и 5
3 и 4
Задание №3
В каком примере допущена ошибка? Объяснить.
А) 3,7 + 1,2 = 4,9 Б) 7,34 + 10,1 = 17,35
В) 4,2 – 2,03 = 2,17 Г) 8,95 – 0,6 = 8,89
Задание №4
Впишите знаки действий:
а) 8,8 * 10 = 88; б) 3,3 : 100 = 0,033; в) 7,5 * 100 = 750.
Задание №5
Запишите пропущенное число:
А) 42, 3 * 10 = 423; б) 0,05 * 100 = 50; в) 3800 * 10 = 380.
Заключение.
Изучив в 5 классе тему «Десятичные дроби», мне захотелось узнать больше, чем написано в учебнике.
Поэтому рассмотрев многие учебники по математике, подобрав необходимый материал в интернете, я ответил на цели и задачи, поставленные ранее, а именно:
· Рассмотрел историю возникновения дробей. Узнал великих математиков, которые внесли новое в определение «десятичная дробь».
· Сформировали умения производить вычисления с десятичными дробями, необходимые для применения в практической деятельности;
Работая над темой данного проекта, по-моему мнению, необходимо было подобрать ряд задач по данной тематике. Такие задачи, которые интересны будут не только для меня, но и для обучающихся 5 классов. Познавательный материал способствует, по- моему мнению, не только выработке умений и закреплению навыков вычислений, но и формирует устойчивый интерес к процессу и содержанию деятельности, а также познавательной и социальной активности. В данной работе я старался показать, что дробь – это постоянный спутник нашей жизни.
Десятичные дроби
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
Пример 2. Перевести 37/1000 в десятичную дробь.
Ответ: 37/1000 = 0,037.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:
Преобразование десятичных дробей
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
Пример 2. Перевести 4,005 в смешанное число.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
Пример 2. Разделить 183,06 на 45.
Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.
Пример 2. Разделить 2,55 на 1 1/3.
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 2/5 на 0,8.
Пример 2. Умножить 0,28 на 6 1/4.
Ответ: 0,28 ∗ 6 1/4 = 0,8.
Урок по теме «Десятичные дроби в нашей жизни»
Ищем педагогов в команду «Инфоурок»
Описание презентации по отдельным слайдам:
«Десятичные дроби в повседневной жизни» 5 класс
Авторы проекта Ученицы 5 «б» класса Кропочева Юлия, Черноморская Юлия. Учитель: В.А.Березка.
Тема исследования «Десятичные дроби в повседневной жизни»
Проблемные вопросы Зачем мы изучаем десятичные дроби? В каких профессиях люди используют десятичные дроби?
Гипотеза исследования Десятичные дроби нужно изучать, потому, что они пригодятся в жизни; Люди многих профессий в своей работе используют десятичные дроби.
Цель исследования Выяснить для каких целей люди используют знания о десятичных дробях.
Задачи исследования Выяснить как относятся ученики нашей школы к вопросу изучения десятичных дробей. Рассмотреть использование десятичных дробей в повседневной жизни.
Результаты исследования Из 47 опрошенных большинство изучают десятичные дроби, потому что это надо по программе для 5 класса. 17 человек знают где используются десятичные дроби. Некоторые изучают их потому, их заставляют родители. Почти половина учеников считают, что эти дроби «не всегда» им помогают в жизни.
В МУЗЫКЕ Нота – целая – делится на половинки, что соответствует музыкальным интервалам в октаву, квинту, кварту. Гармония оказалась тесно связана с дробями.
В медицине Великан из микробов – 0,1мм. Назначение врача: пить по 0,25 таблетки 3 раза в день, в течение 5 дней.
Задания из ЕГЭ с десятичными дробями
№1 Найдите значение выражения (6,7 − 3,2)· 2,4. №2 Найдите значение выражения 0,24·106 :0,6·104 №3 Ивану Кузьмичу начислена заработная плата 20 000 рублей. Из этой суммы вычитается налог на доходы физических лиц в размере 13%. Сколько рублей он получит после уплаты подоходного налога?
№6 Баночка йогурта стоит 14 рублей 60 копеек. Какое наибольшее количество баночек йогурта можно купить на 100 рублей? №7 Килограмм моркови стоит 40 рублей. Олег купил 1 кг 600 г моркови. Сколько рублей сдачи он должен получить со 100 рублей?
№9 Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. ВЕЛИЧИНЫ А) рост ребёнка Б) толщина листа бумаги В) протяжённость автобусного маршрута Г) высота жилого дома ВОЗМОЖНЫЕ ЗНАЧЕНИЯ 1) 32 км 2) 30 м 3) 0,2 мм 4) 110 см В ответе под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Номер материала: ДБ-694896
Международная дистанционная олимпиада Осень 2021
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
В Иркутской области продлили школьные каникулы
Время чтения: 1 минута
СК предложил обучать педагогов выявлять деструктивное поведение учащихся
Время чтения: 1 минута
Путин попросил привлекать родителей к капремонту школ на всех этапах
Время чтения: 1 минута
Заболеваемость ковидом среди студентов и преподавателей снизилась на 33%
Время чтения: 4 минуты
Минобрнауки: вузы вправе вводить QR-коды для посещения корпусов
Время чтения: 2 минуты
В школе в Пермском крае произошла стрельба
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.