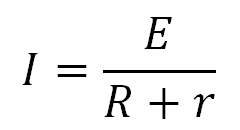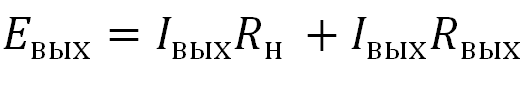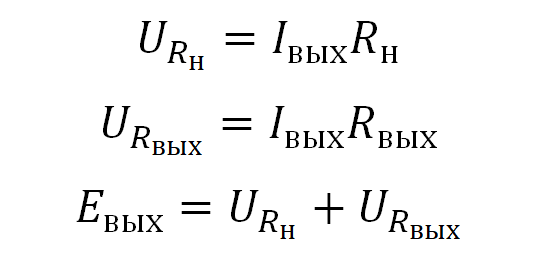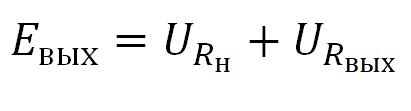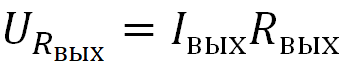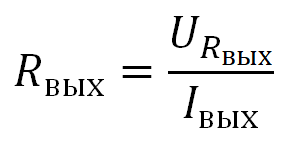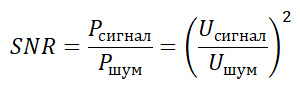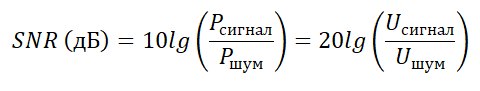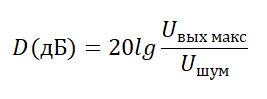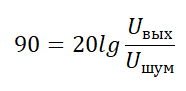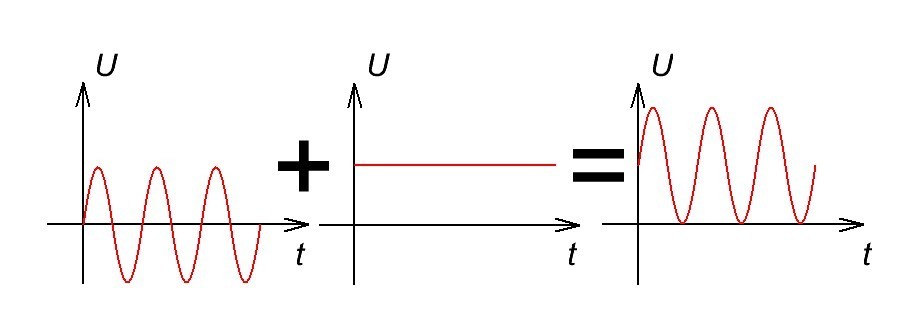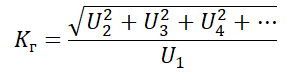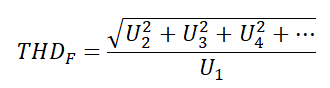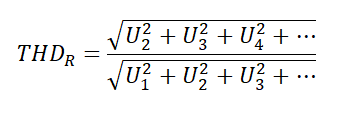зачем нужны частотные характеристики

Аудиофилия. И это все о ней. АЧХ.

Почему мы до сих пор спорим о качестве звука? Казалось бы все очень просто! Все свойства звука, как звуковой волны, давно изучены. Звуковоспроизводящая аппаратура все совершеннее. Но одни меломаны упорно не верят в прогресс и предпочитают проверенные временем форматы и технику. Другие уповая на технические характеристики — убеждены что нашли формулу идеального звука.

Причины, как мне кажется лежат не совсем в плоскости науки и техники. Хотя многое можно описать цифрами и формулами, кроме одной важной составляющей аудиосистемы — человека. И несмотря на то, что наука дает ответ на взаимодействие органов чувств на ощущения звука, мы все равно слышим одно и тоже по разному. В силу субъективных причин (то есть присущих определенному субъекту и не обязательно — другому) обрабатываем звуковую информацию по разному. А уж интерпретируем, вообще, «кто во что горазд»!

Глава первая: Что же такое АЧХ?

Попытаюсь внести ясность в вопрос влияния одной из самых известных и важный характеристик аудиоаппартуры — Ампилитудно частотной характеристики (далее АЧХ) на воприятие звука.

Неофиты аудиофилы или меломаны, не желающие развивать свои знания в области звука уверены, что именно АЧХ способна описать звук! И мало того, ее ширина и равномерность залог правильного звука.

Что же представляет из себя эта почитаемая аудиофилами характеристика?

Если коротко, то она описывает зависимость уровня звукового давления (то есть амплитуды) от частоты. А если совсем просто, то громкость звука определенной частоты при подачи сигнала одного уровня.

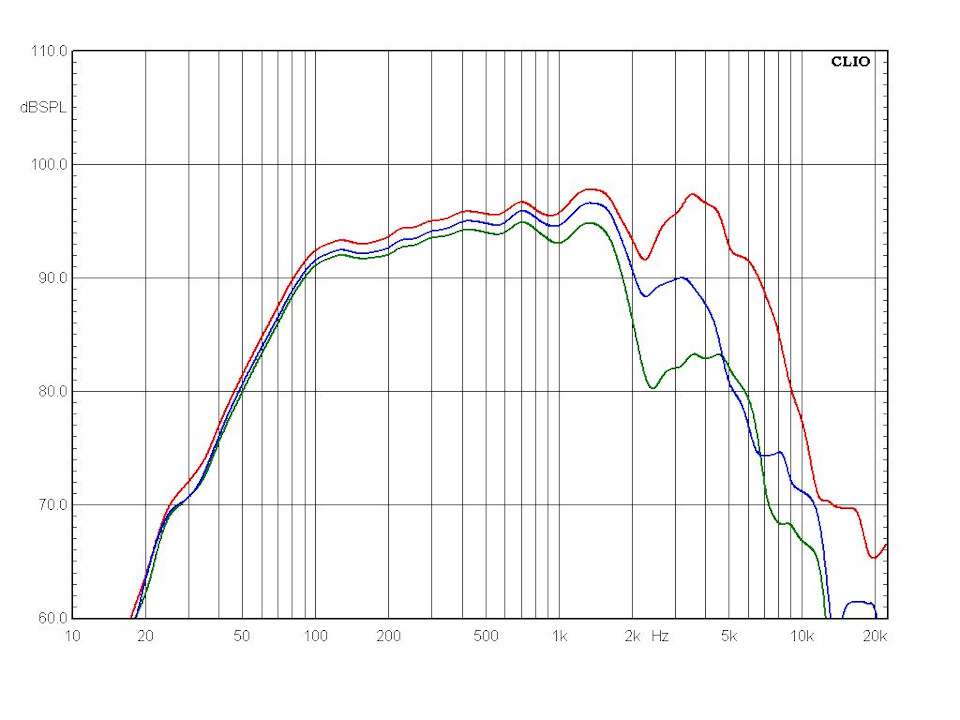
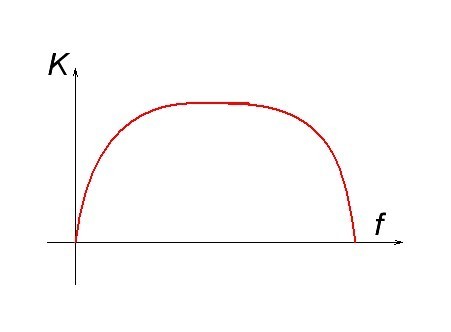
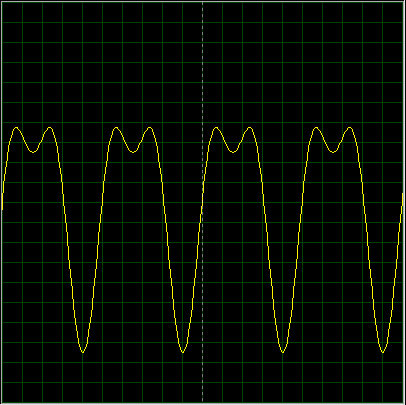
И все бы ничего если бы в реальной технике встречалась плоская и неискаженная АЧХ. Но в жизни мы видим не это:

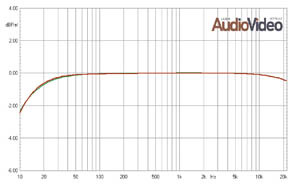
Но это АЧХ, акустических систем, воскликнет «продвинутый» читатель и будет прав! АЧХ же усилителя обычно выглядит так:

Но тем не менее даже твердолобые знают, что разные и имеющие близкие к идеальной АЧХ усилители, звучат по-разному!

Об этом в другой раз. Сейчас же о том, почему АЧХ не в состоянии до конца описать звучание.

Конечно, взаимосвязь АЧХ — звук существует, но не совсем прямая. Точнее, даже не так. Взаимосвязь «АЧХ — тональный баланс» почти линейная. Но все равно с некоторыми оговорками.

Для понимание, что ровная АЧХ и достоверное воспроизведение тембра не одно и тоже мои рассказ.

Многие ошибаясь, предполагают, что тембр это звучание сигнала определенной частоты. Нет, дорогие мои, высота звука — вот звучание сигнала определенной частоты, иначе говоря тон! А тембр это набор определенных частот (тонов и обертонов) характерных для определенного инструмента, звука.

Казалось бы, логично предположить достоверно воспроизведем весь спектр звука — достоверно воспроизведем любой тембр.

Но даже в этом есть свои сложности!

Глава вторая: Музыка не синусоида!

Основная проблема — тембр любого музыкального инструмента (мы ведь музыку будем слушать?) ни нечто статическое, а он имеет характерные только ему изменения во времени. То есть нарастания (атака) и затухания сигнала.

А это уже АЧХ не описывает! А вот аппаратура, ой как по-разному способна передавать атаку и затухание звука.

Второй важный момент — Тембр это не только основной тон, в его состав входят обертоны. То есть незначительные по уровню (по сравнению с основным тоном) тоны, характерные только для этого инструмента или голоса.

Опять же вроде ничего сложного нет, если ровно воспроизвести все частоты, то тоны и обертоны не пострадают. Но! Дело в том, что обертоны имеют отличный (более низкий) уровень по сравнению с основным. И аппаратура уже не так линейно воспроизводит сигнал меньших уровней. И чем уровень ниже, тем кривее АЧХ мы имеем.

Обычной АЧХ это тоже не описать.

Глава третья: Психоакустика — лженаука? Или обмануть меня не сложно, я сам обманываться рад!

«Технари от звука» не верят во влияние восприятия звука нашим мозгом от определенных условий. Они априори считают, что мозг это спектроанализатор и мы слышим звуки, так же как их фиксирует измерительная техника.

Но слух можно, а иногда и нужно обмануть! Например плавный и равномерный спад на краях АЧХ, то есть на высоких и низких частотах слух переносит легче и воспринимает АЧХ, как более широкую. А при резких скачках и спадах «обрезает» воспринимаемую АЧХ.

Тихие звуки маскируются более громкими. Если громкость звука резко падает, то человек на мгновение «глохнет».

Искажения на средних частотах более заметны ухом.

Так что зная эти законы (а поверьте производители их знают) можно сделать звучание компонента с более узким АЧХ не только благозвучней, но и субъективно шире, чем при прослушивании аппарата имеющего более широкую, но резко обрезанную АЧХ.

Заключение: АЧХ от Лукавого.

Получается, что АЧХ вообще не нужна? И она ничего не описывает? Если пытаться заменить «чтением» АЧХ прослушивание — несомненно! Если использовать, как инструмент дополняющий прослушивание, то почему бы и нет. Но полностью строить выводы на ее основе, как мы видим, не точнее чем предсказывать погоду. Вроде и взаимосвязь есть и опыт подсказывает, что май — не месяц снегопадов, однако реальная жизнь преподносит сюрпризы, а слух говорит о том, что криво на графиках, не всегда плохо на слух.

Источник

Зачем нужен анализатор частотных характеристик

Одним из методов оценки состояния механической и электрической целостности сердечника силового и распределительного трансформатора, а также его обмоток, является анализ частотной характеристики развертки или SFRA. Это высокочувствительный сравнительный метод, основанный на измерениях передаточных функций электрического тока в широком диапазоне частот. Анализ может применяться после перемещений силовых и распределительных трансформаторов, при вводе их в эксплуатацию и в послеаварийных испытаниях, особенно информативным он является после воздействия высоких токов короткого замыкания.

С помощью анализа частотной характеристики возможно обнаружение деформации обмотки или ее частичного нарушения, получение информации о смещении сердечника, выявление смещений между обмотками высокого и низкого напряжения, а также обнаружение короткого замыкания или обрыва витков. Среди прочего, по результатам SFRA можно говорить о проблемах с подключением обмоток, сломанных зажимных конструкциях, неисправном заземлении или о проблемах с подключением.

Реализация данного метода возможна, например, с использованием анализатора частотной характеристики с разверткой DV Power FRA500. Устройство представляет собой портативный цифровой прибор, который управляется с помощью предварительно установленного на компьютер программного обеспечения от производителя. Методы измерения подробно представлены в ГОСТ Р 59239-2020 «Трансформаторы силовые и реакторы. Метод измерения частотных характеристик».

Оценка результатов анализа частотных характеристик

Оценка полученных результатов частотной характеристики развертки проводится путем сравнения результата с эталонными значениями, которыми могут являться полученные ранее результаты измерений конкретного устройства, либо результаты частотных характеристик идентичного трансформатора, а также возможно сравнение результатов, полученных с разных фаз одного трансформатора. При тестировании трансформатора в широком диапазоне частот получают уникальный сигнал, который строится в виде графика. Этот график отражает изменение емкости, которое возникает при любом механическом изменении или нарушение электрической целостности, так как эти процессы ведут к изменению сопротивления и индуктивности.

Для анализа частотной характеристики развертки подается синусоидальный сигнал с постоянной амплитудой и переменной частотой. Например, на приборе DV Power FRA500 напряжение может варьироваться от 0,2 до 24 В, а диапазон рабочих частот изменяется от 0,1 Гц до 25 МГц. Данный сигнал подается с одной стороны обмотки, на выходе снимается значение амплитуды и фазового угла выходного сигнала, на основании этих данных строится график зависимости амплитуды от частоты и фазы от частоты, оба графика выводятся на одном рисунке.

Значительная погрешность измерений частотных характеристик может быть вызвать неправильным или некачественным соединением основных и заземляющих устройств. Для получения достоверных результатов также необходимо соблюдать идентичность подключаемых коаксиальных кабелей между клеммами обмоток и самим измерительным прибором.

Стоит отметить, что время построения частотной характеристики на приборе DV Power FRA500 составляет около 20 секунд, а также с помощью этого же прибора возможно провести проверку заземления и целостности кабельных соединений, результаты измерений возможно экспортировать в форматы XML и XLS. Но что важнее, программное обеспечение дает возможность сразу определить коэффициенты корреляции, использование которых рекомендовано при интерпретации результатов измерений согласно ГОСТ Р 59239-2020.

Источник

частотная характеристика

Частотные характеристики разомкнутой системы.

часто́тная характери́стика в теории автоматического регулирования — зависящий от частоты комплексный коэффициент связи между рассматриваемым параметром системы и входным воздействием; Ч. х. существуют, если вынужденная составляющая движения системы является периодической функцией одного периода (одной частоты ω) с периодом вынуждающего воздействия. Если входной сигнал (воздействие) x_вх и выходной сигнал (отклик на воздействие) x_вых системы представить в комплексном виде:

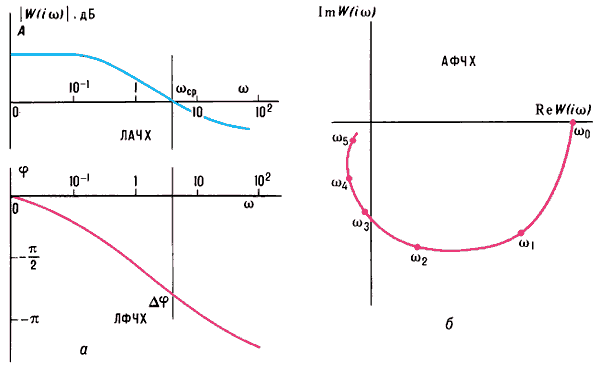
где A_вх(ω), A_вых(ω) — амплитуды, φ_вх(ω), φ_вых(ω) — фазы соответственно входного и выходного сигналов, то отношение W(iω) = x_вых/x_вх системы; при этом величину |W(iω)| = A_вых(ω)/A_вх(ω) называют амплитудно-частотной характеристикой (АЧХ), а величину arga W(iω) = φ_вых(ω)-φ_вх(ω) — фазовой частотной характеристикой (ФЧХ). В практике часто используют логарифмические амплитудно-частотные характеристики (ЛАЧХ) и логарифмические фазовые частотные характеристики (ЛФЧХ). При их построении по осям абсцисс откладывают частоту в логарифмическом масштабе, а по осям ординат |W(iω)|, — выраженную в дБ, и φ в линейном масштабе (см. рис., а). При этом частота среза ω_ср, при которой ЛАЧХ пересекает ось абсцисс, может служить мерой быстродействия системы, а запас по фазе ∆φ(∆φ = π-|φ(ω_ср)|) — мерой затухания свободных колебаний в ней. Функцию W(iω), построенную на комплексной плоскости в координатах ReW(iω), ImW(iω) (см. рис., б), называют амплитудно-фазовой частотной характеристикой (см. также Годографа метод). Для нелинейных систем за A_вых и φ_вых принимаются амплитуда и фаза первой гармоники выходного сигнала. В этом случае Ч. х. зависит от амплитуды входного сигнала, а при некоторых сочетаниях параметров системы — и от направления (увеличения или уменьшения, см., например, Гистерезис) изменения частоты. Изложенное выше справедливо для так называемых непрерывных стационарных систем; в более общем случае линейных непрерывных и импульсных систем Ч. х. определяют как отношение комплексных спектров выходного и входного сигналов. У системы, имеющей n параметров состояния и k входных воздействий, насчитывается n·k независимых Ч. х. Например, короткопериодическое продольное движение самолёта характеризуется изменениями угла атаки α и скорости тангажа ω_z; самолёт имеет четыре Ч. х. по этим параметрам при отклонении δ_в руля высоты и воздействии вертикальных порывов ветра со скоростью W, являющиеся функциями iω: α/δ_в, α/W, ω_z/W, а комбинациями этих Ч. х. являются Ч. х. по перегрузке n_y: n_y/δ_в, n_y/W.

Ч. х. широко используются при анализе системы «самолёт—лётчик—система управления» благодаря возможности определения её динамических характеристик по Ч. х. отдельных элементов, устанавливаемых расчётными или экспериментальными методами. Ч. х. применяются для определения запасов устойчивости замкнутых систем по Ч. х. разомкнутых, для выяснения параметров автоколебаний при наличии в системах нелинейностей и реакции систем на детерминированные и случайные воздействия, для математического моделирования элементов систем по их Ч. х. В общем случае Ч. х. системы связана с её передаточной функцией W(p) соотношением W(iω) = W(p)_{p = ω}.

Широкое использование экспериментальных методов определения Ч. х. привело к созданию и внедрению в исследовательскую практику специализированных приборов — анализаторов Ч. х., включающих генераторы гармонических сигналов, измерительные и вычислительные устройства.

Литература:
Техническая кибернетика. Теория автоматического регулирования, под ред. В. В. Солодовникова, кн. 1—3, М., 1967—69.

Полезное

Смотреть что такое «частотная характеристика» в других словарях:

Частотная характеристика — Источник: ГОСТ 21878 76: Случайные процессы и динамические системы. Термины и определения оригинал документа Смотри также родс … Словарь-справочник терминов нормативно-технической документации

частотная характеристика — электровакуумного прибора; частотная характеристика; отрасл. инерционная характеристика Зависимость какого либо параметра электровакуумного прибора или режима от частоты изменения какого либо другого параметра режима (частоты напряжения, частоты… … Политехнический терминологический толковый словарь

частотная характеристика — Зависимость параметров синусоидальных колебаний выходной координаты линейного объекта от параметров синусоидальных колебаний входной координаты, полученная для установившихся режимов функционирования. [Сборник рекомендуемых терминов. Выпуск 107.… … Справочник технического переводчика

Частотная характеристика — в теории автоматического регулирования зависящий от частоты комплексный коэффициент связи между рассматриваемым параметром системы и входным воздействием; Ч. х. существуют, если вынужденная составляющая движения системы является периодической… … Энциклопедия техники

Частотная характеристика — Амплитудно фазовая частотная характеристика (АФЧХ) удобное представление частотного отклика линейной стационарной динамической системы в виде графика в полярных координатах. На таком графике частота выступает в качестве параметра кривой, фаза и… … Википедия

частотная характеристика — dažninė charakteristika statusas T sritis automatika atitikmenys: angl. frequency characteristic; frequency domain; frequency response characteristic; frequency response characteristic; harmonic response; harmonic response characteristic;… … Automatikos terminų žodynas

частотная характеристика — dažninė charakteristika statusas T sritis Standartizacija ir metrologija apibrėžtis Kreivė, vaizduojanti įrenginio, įtaiso ir pan. išėjimo dydžio vertės priklausomybę nuo įėjimo dydžio dažnio. atitikmenys: angl. frequency characteristic;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

частотная характеристика — harmoninio atsako charakteristika statusas T sritis Standartizacija ir metrologija apibrėžtis Tam tikro įtaiso ar grandinės, kurią veikia harmoniniai virpesiai, atsako priklausomybė nuo dažnio. atitikmenys: angl. frequency response… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

частотная характеристика — dažninė charakteristika statusas T sritis fizika atitikmenys: angl. frequency characteristic vok. Frequenzgang, m; Frequenzkennlinie, f rus. частотная характеристика, f pranc. caractéristique fréquentielle, f … Fizikos terminų žodynas

частотная характеристика — harmoninio atsako charakteristika statusas T sritis fizika atitikmenys: angl. frequency response characteristic; harmonic response characteristic vok. Frequenzgangcharakteristik, f; harmonische Frequenzcharakteristik, f rus. частотная… … Fizikos terminų žodynas

ЧАСТОТНАЯ ХАРАКТЕРИСТИКА — характеристика, выражающая зависимость амплитуды, фазы, чувствительности или к. л. параметра линейной динамической системы от частоты поступающего на её вход синусоидального колебания. Различают амплитудно частотную характеристику, фазочастотную… … Большой энциклопедический политехнический словарь

Источник

Амплитудно-частотная и Фазо-частотная характеристика

Аббревиатура АЧХ расшифровывается как амплитудно-частотная характеристика. На английском этот термин звучит как «frequency response», что в дословном переводе означает «частотный отклик». Амплитудно-частотная характеристика цепи показывает зависимость уровня сигнала на выходе данного устройства от частоты передаваемого сигнала при постоянной амплитуде синусоидального сигнала на входе этого устройства. АЧХ может быть определена аналитически через формулы, либо экспериментально. Любое устройство предназначено для передачи (или усиления) электрических сигналов. АЧХ устройства определяется по зависимости коэффициента передачи (или коэффициента усиления) от частоты.

Классическим методом измерения АЧХ является подача на вход исследуемого объекта гармонического сигнала измеряемой частоты с постоянной или известной для каждой частоты сигнала амплитудой. В этом случае измеряется отношение модулей амплитуды выходного и входного сигналов (коэффициента передачи) исследуемой системы для разных частот.

Объясняя простыми словами, на вход устройства подаем сигнал с заданной частотой и известной амплитудой, на выходе этого устройства частота будет такая же, что и на входе, а вот амплитуда этого сигнала изменится. Отношение выходного значения амплитуды к значению на входе и будет являться амплитудно-частотной характеристикой.

Для наглядного отображения покажем как рассчитывается коэффициент передачи. Коэффициент передачи – это отношение напряжения на выходе цепи к напряжению на ее входе. Или формулой

Фазо-частотная характеристика (ФЧХ) – зависимость разности фаз между выходным и входным сигналами от частоты сигнала, функция, выражающая (описывающая) эту зависимость, также – график этой функции.

– Для линейной электрической цепи, зависимость сдвига по фазе между гармоническими колебаниями на выходе и входе этой цепи от частоты гармонических колебаний на входе.

Часто ФЧХ используют для оценки фазовых искажений формы сложного сигнала, вызываемых неодинаковой задержкой во времени его отдельных гармонических составляющих при их прохождении по цепи

Источник

Основные параметры усилителя

Каждый электронщик должен знать основные параметры усилителя, так как усилитель в электронике используется абсолютно везде. В этой статье мы рассмотрим самые важные параметры усилителей.

Входное и выходное сопротивление

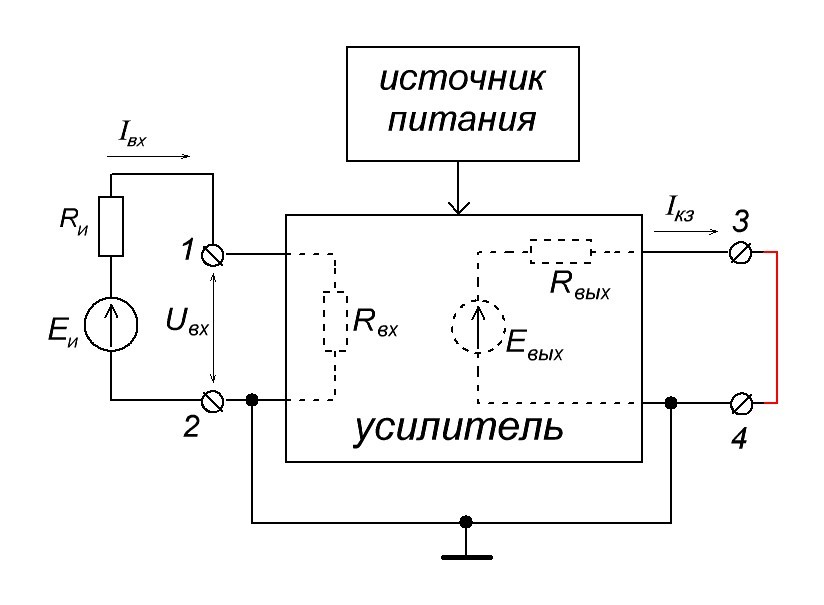
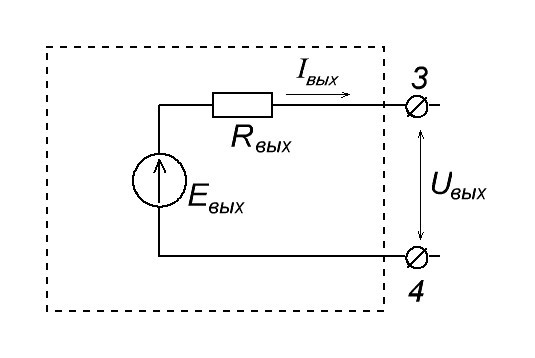
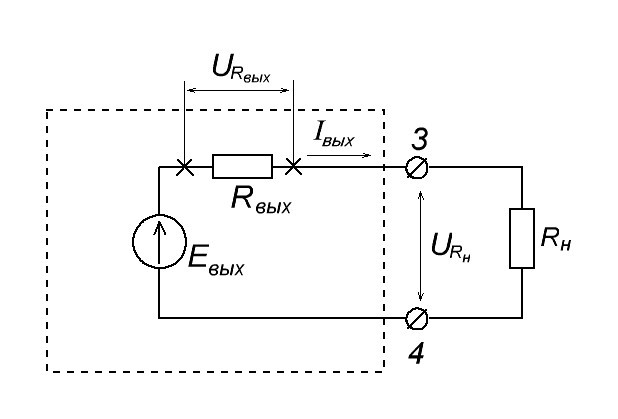
Кто в первый раз сталкивается с этими понятиями, читайте эту статью. Кому лень читать, вкратце объясню здесь из прошлой статьи. Каждый усилительный каскад имеем свое входное и выходное сопротивление. На схеме R_вх и R_вых

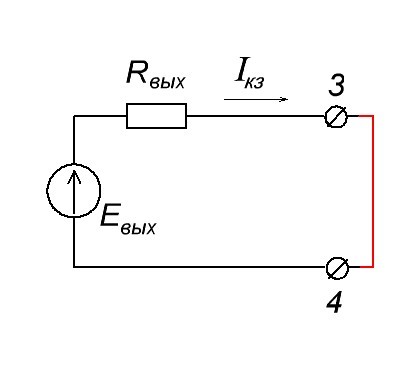
Немного иначе обстоят дела с выходным сопротивлением. В теории, можно замкнуть выходные клеммы 3 и 4 накоротко. В этом случае во выходной цепи усилителя у нас появится ток короткого замыкания I_кз

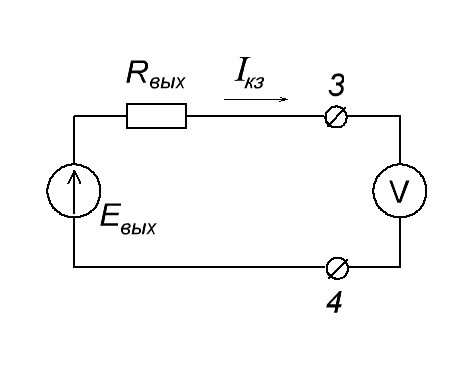
Выходное сопротивление усилителя можно найти двумя способами: теоретическим и практическим. Теоретический способ, часто сложен, поскольку неизвестны многие параметры «черного ящика», называемого усилителем. Проще определить выходное сопротивление практическим путем.

Как найти выходное сопротивление на практике

Если вы не забыли, мультиметр в этом случае нам покажет ЭДС E_вых , т. е. в данном случае E_вых = U_вых . (Что такое ЭДС).

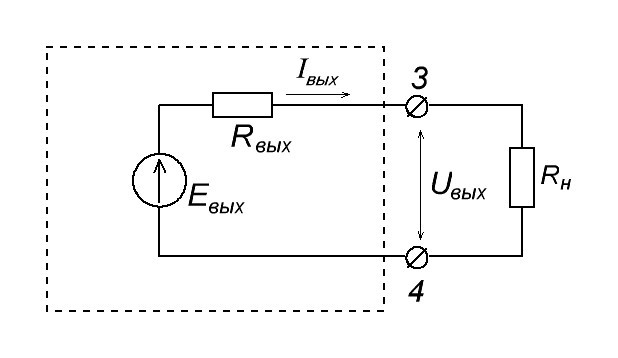
Номинал нагрузочного сопротивления должен выбираться исходя из допустимого тока и мощности усилителя.

Выходная мощность усилителя 10 Вт, допустимое выходное напряжение (эффективное) 100 В. В этом случае, резистор нагрузки должен иметь сопротивление не менее R=U 2 /P = 10000/10 = 1 кОм. Мощность резистора: P_R = U 2 /R = 10000/1000 = 10 Вт

Какой же физический смысл этого опыта? В результате этих шагов, у нас цепь станет замкнутой, а два сопротивления, R_вых и R_н , образуют делитель напряжения. Сюда же можно приписать закон Ома для полной цепи, который выражается формулой:

I — сила тока в цепи, А

R — сопротивление нагрузки, Ом

r — внутреннее сопротивление источника ЭДС, Ом

Применительно к нашей ситуации, формула будет иметь такой вид:

Или словами, ЭДС равняется сумме падений напряжения на каждом сопротивлении.

Шаг номер 3: Замеряем напряжение на нагрузке U_Rн. Вспоминаем формулу выше:

Далее что нам требуется — это увеличивать входное напряжение и снимать выходное напряжение — так мы увидим всю нелинейность выходной характеристики от тока и сможем замерить выходное сопротивление в диапазоне нагрузок, так как большинство усилителей мощности имеют нелинейность выходного сопротивления от допустимого тока нагрузки.

Коэффициент усиления

Про коэффициенты усиления мы писали еще в прошлой статье.

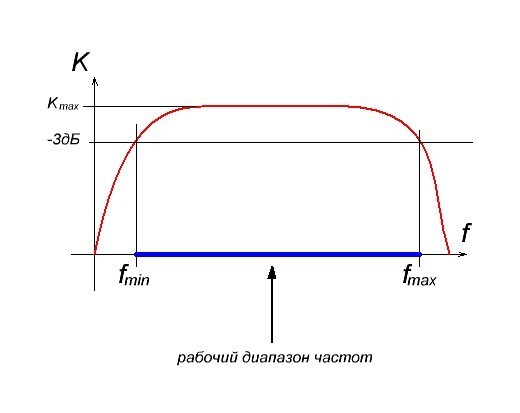
Рабочий диапазон частот

Собственные шумы усилителя.

В электронике шумом называют беспорядочные колебания амплитуды сигнала, которые глушат полезный сигнал. Сюда же относятся разного рода помехи. Собственные шумы усилителя — это шумы, которые зарождаются как внутри самого усилителя, так и могут быть вызваны внешним источником помех, либо некачественным питанием усилителя. Давайте рассмотрим основные виды шумов усилителя.

Этот шум вызван некачественным питанием усилителя. Если источник питания собран на сетевом трансформаторе, то шум будет на частоте 100 Гц (2х50Гц, по схеме диодного моста). То есть на выходе такого усилителя мы услышим гудение, если подцепим к выходу динамик. Думаю, вы часто слышали такое выражение «что-то динамики фонят». Это все из этой серии.

Помехи и наводки

Это могут быть внешние источники, которые так или иначе действуют на усилитель. Это может быть наводка от сети 220 Вольт (очень часто ее можно увидеть, если просто прикоснуться к сигнальному щупу осциллографа), это также может быть какая-либо искра, которая образуется в свечах двигателей внутреннего сгорания.

Небольшое лирическое отступление. Помню, как смотрел диснеевские мультики по первому каналу, а через дорогу сосед пилил дрова с помощью бензопилы Дружба-2. Тогда на экране ТВ были такие помехи, что я про себя тихо материл соседа.

Ну а как же без грозовых разрядов? Благодаря электромагнитному импульсу у нас появилось такое изобретение, как радио.

К источникам помех можно также отнести радио- и ТВ-станции, рядом лежащее и стоящее электрооборудование, типа мощных коммутационных механических ключей, разрядников и тд.

Ну и конечно, это шум самих радиоэлементов. Сюда относится тепловой шум (джонсоновский), дробовой шум, а также фликкер-шум.

Наиболее существенными являются шумы, которые возникают на входе усилителя в самом первом каскаде. Этот шум в дальнейшем усиливается также, как и входной полезный сигнал. В результате на выходе усилителя у нас будет усилен как полезный сигнал, так и шумовой. Поэтому, при проектировании качественных усилителей стараются как можно сильнее минимизировать шум на входе первого каскада усилителя.

Отношение сигнал/шум

Пусть у вас дома стоит телевизор, который ловит аналоговое вещание. На экране телевизора мы видим четкую картинку:

Но вдруг антенна на крыше вашего дома из-за сильного ветра чуток отклонилась в сторону и изображение ухудшилось

Потом антенна вообще упала с крыши, и на телевизоре мы видим теперь что-то типа этого

В каком случае отношение сигнал/шум будет больше, а в каком меньше? На первой картинке, где четкое изображение, отношение сигнала к шуму будет очень большое, так как не первой картинке мы простым взглядом не можем уловить каких-либо помех на изображении, хотя по идее они есть).

На второй картинке мы видим, что в изображении появились помехи, которые делают некомфортным просмотр картинки. Здесь отношение сигнала к шуму уже будет намного меньше, чем на первой картинке.

Отношение сигнал/шум является количественной безразмерной величиной.

В аналоговой электронике для нормальной работы усилителя полезный сигнал должен в несколько раз превышать шумы, иначе это сильно скажется на качестве усиления, так как полезный сигнал суммируется с шумовым.

Отношение сигнал/шум в англоязычной литературе обозначается как SNR или S/N.

Так как порой это отношение достигает очень больших значений в цифрах, поэтому чаще всего его выражают в децибелах:

U_cигнал — среднеквадратичное значение полезного сигнала, В

U_шум — среднеквадратичное значение шумового сигнала, В

P_сигнал — мощность сигнала

То есть в нашем случае с котиком на первой картинке амплитуда полезного видеосигнала в разы превосходила амплитуду шума, поэтому первая картинка была четкой. На третьей картинке амплитуда полезного видеосигнала почти была равна амплитуде шума, поэтому картинка получилась очень зашумленной.

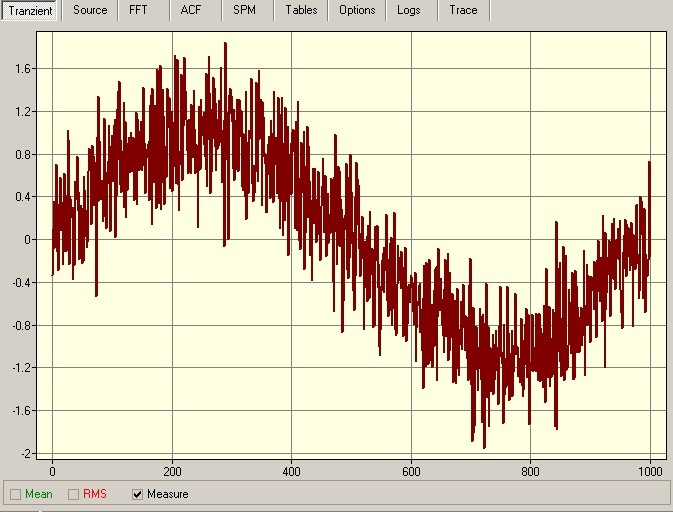
Еще один пример. Вот синусоидальный сигнал с SNR=10:

А вот тот же самый синус с SNR=3

Как вы могли заметить, сигнал с SNR=10 намного «чище», чем с SNR=3.

SNR чаще всего можно увидеть при описании характеристик усилителя звука. Чем выше SNR, тем лучше по качеству звучания будет усилитель. Для HI-FI систем звучания этот показатель должен быть от 90 дБ и выше. Для телефонных разговоров вполне достаточно и 30 дБ.

На практике SNR измеряется на выходе усилителя с помощью милливольтметра с trueRMS, либо с помощью анализатора спектра.

Амплитудная характеристика

Амплитудная характеристика усилителя — это зависимость амплитуды сигнала на выходе от входного сигнала при фиксированной частоте. Обычно она составляет 1 кГц.

Амплитудная характеристика идеального усилителя по идее должна выглядеть вот так:

Это луч, который начинается от нулевой точки отсчета координат и простирается в бесконечность.

Но на самом деле реальная амплитудная характеристика усилителя выглядит вот так:

Динамический диапазон усилителя

Динамический диапазон — это отношение максимально допустимого уровня выходного сигнала к его минимальному уровню, при котором обеспечивается заданное отношение сигнал/шум:

Чтобы понять концовку определения «обеспечивается заданное отношение сигнал/шум» динамического диапазона, давайте рассмотрим наш рисунок:

Допустим, наш усилитель должен иметь SNR=90 дБ. Будет ли правильно, если мы возьмем U_{вых мин} за U_шум?

Конечно же нет! В этом случае в этой точке на графике амплитуды сигнала и шума будут равны, а следовательно, по формуле

получим, что SNR=0 дБ.

Допустим, что U_шум =1 мкВ, подставляем в формулу

Из этого уравнения находим U_вых . Это будет как раз являться U_{вых. мин.} для формулы:

при SNR=90. В нашем случае это будет точка А.

U_{вых макс} берем в точке B, так как в этом случае это максимальное значение, при котором у нас в усилителе не возникают нелинейные искажения (о них чуть ниже).

Рабочая область усилителя будет обеспечиваться на отрезке АВ. В этом случае у нас будут минимальные искажения в сигнале, так как эта область линейная. Отношение максимально допустимого выходного сигнала к уровню шума — это предельный уровень динамического диапазона для аналогового усилителя.

Для усилителей звука выход за пределы этой рабочей области в большую сторону будет чреват нелинейными искажениями, а в меньшую — полезный сигнал задавят помехи. Да вы и сами, наверное замечали, что выкрутив на полную катушку ручку громкости дешевой китайской магнитолы, у нас качество звучания оставляло желать лучшего, так как в дело «вклинивались» нелинейные искажения.

Коэффициент полезного действия (КПД)

КПД представляет из себя отношение мощности на нагрузке усилителя к мощности, которая потребляется усилителем от источника питания

P_вых — это мощность на нагрузке, Вт

P_и.п. — мощность, потребляемая источником питания, Вт

Искажения, вносимые усилителем

Искажения определяют сравнением формы сигнала на входе и на выходе. Идеальным является усилитель, который в точности повторяет форму сигнала, поданного на вход. Но так как наш мир не идеален, и радиоэлементы тоже не идеальны, то и на выходе у нас сигнал будет всегда немного искаженный. Главное, чтобы эти искажения не были столь критичны.

В основном искажения делятся на 4 группы:

Частотные искажения

Частотные искажения возникают вследствие того, что коэффициент усиления во всем диапазоне частот не одинаковый. Или простыми словами, какие-то частоты усиливаются хорошо, а какие-то плохо). Чтобы в этом разобраться, достаточно посмотреть на АЧХ усилителя.

В данном случае мы можем увидеть, что низкие и высокие частоты будут усиливаться меньше, чем средние частоты. А так как сложный сигнал состоит из множества частотных составляющих, вследствие этого и возникнут частотные искажения.

Фазовые искажения

Фазовые искажения возникают из-за того, что разные частоты с разной задержкой по времени появляются на выходе усилителя. Какие-то частоты запаздывают больше, а какие-то меньше. Давайте все это рассмотрим на примере двух картинок.

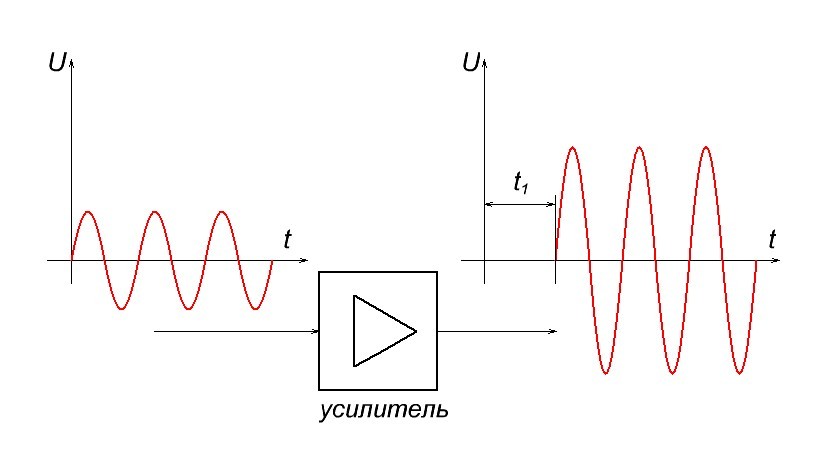
Допустим, мы «загоняем» на вход синусоидальный сигнал с низкой частотой и на выходе получаем уже усиленный сигнал, но немного с небольшой задержкой.

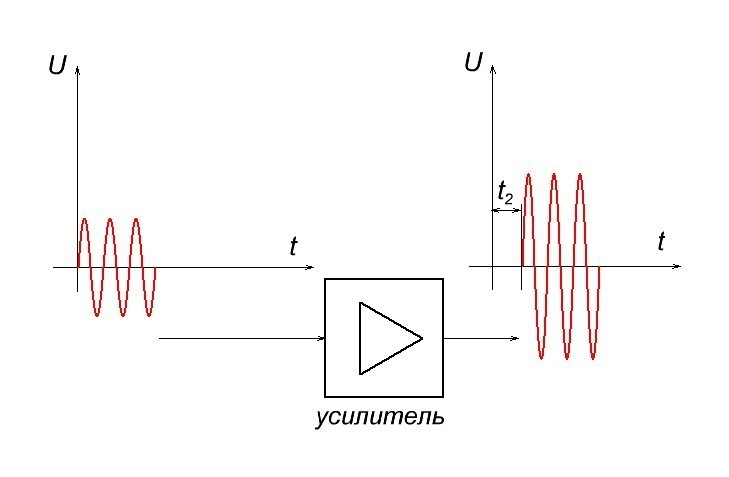
Но также не забывайте, что катушки и конденсаторы являются частото-зависимыми радиоэлементами. Их реактивное сопротивление зависит от частоты сигнала, поэтому, прогоняя через усилитель сигнал с другой частотой, мы получим уже совсем другую задержку сигнала

То есть в нашем случае t₁ ≠ t₂ . Хорошо это или плохо? Если мы будем усиливать синусоиду, то в принципе нам по барабану. Какая разница раньше он появится на выходе или позже? Главное то, что сигнал будет усиленный.

Все бы ничего, но стоит помнить, что сложные сигналы состоят из суммы множества синусоид различных частот и амплитуд.

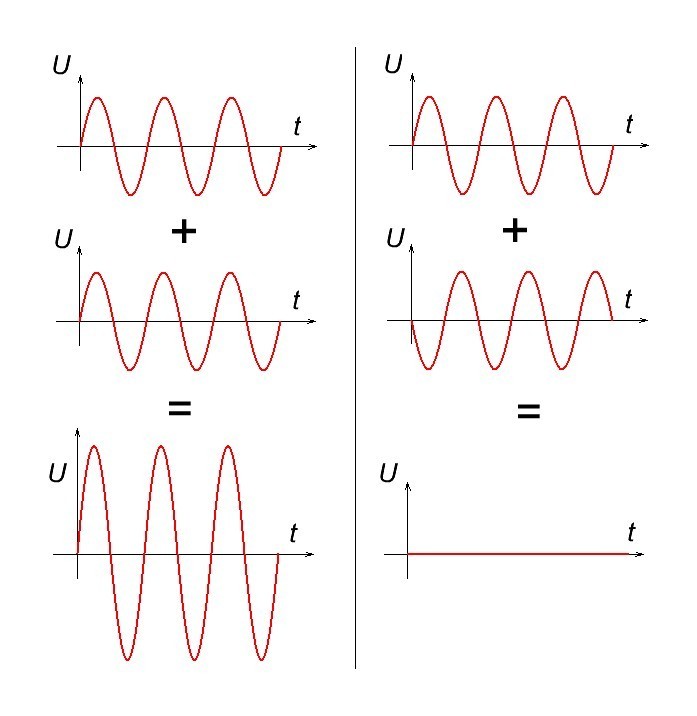
Чтобы понять, что такое сумма сигналов, достаточно рассмотреть вот такие примеры:

ну и еще один, мне не жалко)

Складываем амплитуды в одинаковые моменты времени и получаем сумму этих двух сигналов.

А вот так из разных синусоид разных частот складывается прямоугольный сигнал:

В данном случае мы пытаемся «собрать» прямоугольный сигнал из суммы синусоид разных амплитуд и частот.

Но так как у нас усилитель задерживает разные сигналы по частоте по-разному, то у нас между сигналами происходит разнобой. Лучше всего это объяснит рисунок ниже. Имеем два синусоидальных сигнала с разной частотой и амплитудой:

Если их сложить, получим сложный сигнал:

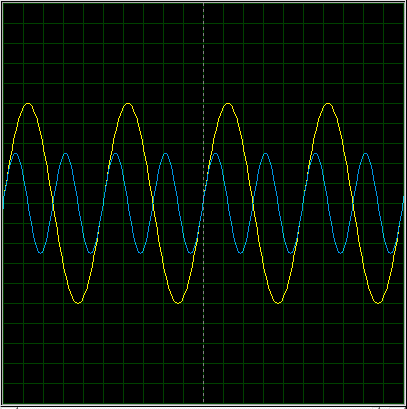
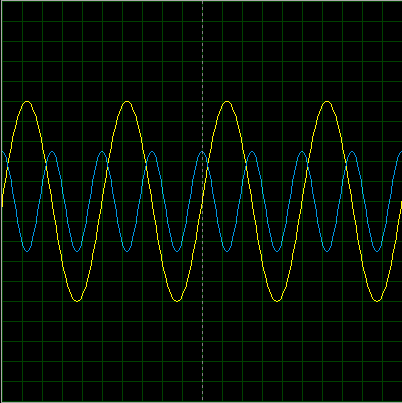
Но что будет, если второй сигнал сдвинется по фазе относительно первого?

Смотрим теперь сумму этих сигналов:

Абсолютно другой сигнал! Чувствуете разницу? Чуток сдвинули фазу, а форма сигнала уже поменялась.

То есть на выходе усилителя мы хотели получить вот такой усиленный сигнал:

В результате фазовых искажений наш сложный сигнал, состоящий из двух синусоид, поменял форму. На выходе усилителя мы получили совсем другой сигнал. А как вы помните, роль усилителя заключается в том, чтобы усиливать сигнал, сохраняя при этом его форму.

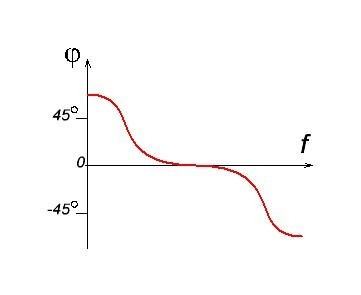
Фазо-частотная характеристика (ФЧХ) усилителя — это график зависимости угла сдвига фаз, вносимого усилителем, от частоты. Выглядеть она может примерно вот так:

φ — это сдвиг фазы относительно входного и выходного сигнала

f — частота сигнала

Человеческое ухо не замечает фазовых искажений, несмотря на то, что даже изменяется форма сигнала. Поэтому при проектировании звуковых усилителей фазовые искажения не принимают во внимание.

Частотные искажения и фазовые искажения относят к линейным искажениям, так как оба вида искажений обусловлены линейными элементами схемы. Если сказать по научному, у нас в спектре сигнала не появляется дополнительных гармоник.

Переходные искажения

Переходным искажением называют искажение прямоугольного импульса, которое подается на вход усилителя. На выходе такой импульс будет иметь уже другую форму, вызванную искажением сигнала внутри самого усилителя.

Для оценки переходных искажений используют переходную характеристику. Она представляет из себя зависимость напряжения или тока на выходе усилителя от времени от подачи на его вход прямоугольного импульса.

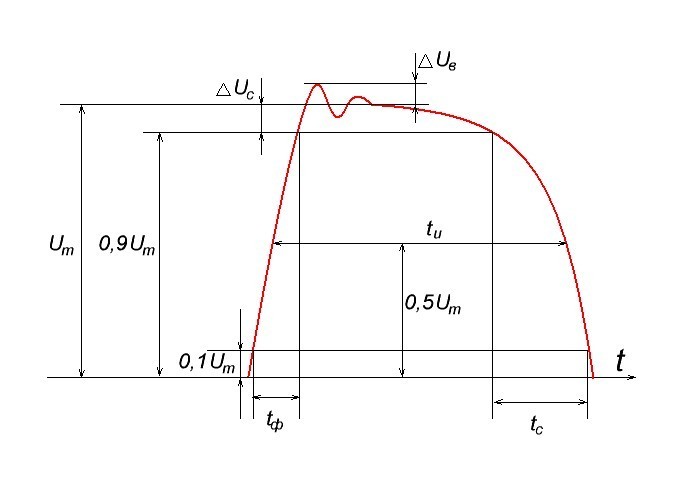
На рисунке ниже имеем прямоугольный сигнал, который подаем на вход усилителя, а на выходе усилителя уже будет искаженный усиленный сигнал. Это искажения вызваны, как обычно, с наличием в схеме усилителя реактивных радиоэлементов, то есть тех же самых катушек индуктивности и конденсаторов.

Для оценки переходных искажений используют такие параметры:

U_m — это амплитуда импульса, отсчитывается от плоской вершины импульса, В

ΔU_в — это выброс фронта импульса, В

Следующие два параметра измеряются в диапазоне от 0,1U_m и до 0,9U_m :

t_ф — длительность фронта импульса

t_c — длительность спада импульса

Нелинейные искажения

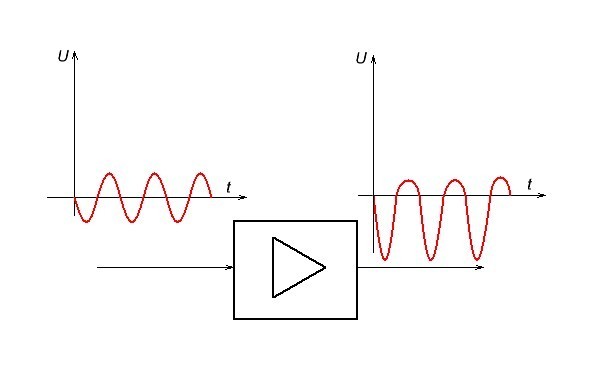
Ну и напоследок мы с вами разберем нелинейные искажения. Нелинейными она называются из-за того, что такие искажения уже меняют форму сигнала, в отличие от линейных искажений. Все дело в том, что электронные лампы и полупроводники имеют нелинейную характеристику. Давайте рассмотрим все это дело более подробно.

Как вы могли заметить, на выходе у нас форма сигнала изменилась. Нашу верхнюю часть синусоиды усиленного сигнала немного «придавило». То есть мы подавали сигнал одной формы, а вышел сигнал совсем другой формы. Это не есть хорошо и с этим надо бороться.

Если сказать более научным радиотехническим языком, в нашем сигнале появились дополнительные гармоники, которых не было в исходном сигнале. В данном случае мы на вход загоняли простой синусоидальный сигнал, состоящий из одной гармоники, а получили на выходе сложный сигнал, состоящий уже из нескольких гармоник.

Для количественной оценки нелинейных искажений используется коэффициент гармонических искажений (КГИ). Он выражается формулой:

Эта величина находится как отношение среднеквадратичного напряжения суммы высших гармоник сигнала, кроме первой, к напряжению первой гармоники при воздействии на вход усилителя синусоидального сигнала.

или на английский манер

Также есть и подобный параметр коэффициент нелинейных искажений (КНИ). Он выражается формулой:

на английский манер

Эти два параметра выражаются в процентах. Для малых значений коэффициенты КГИ и КНИ почти совпадают. Так что коэффициент искажений можно считать как по первой, так и по второй формуле.

Источник