зачем нужны битовые операции
Начинаем изучать STM32: битовые операции
Небольшое отступление.
В прошлом уроке мы рассмотрели с чего начать, если вы решили изучать микроконтроллеры STM32: как настроить IDE, как создать простой проект, как откомпилировать программу и как запустить программу на выполнение. После полюбовались на перемигивание светодиодов на Discovery-плате )
Начиная новую статью, я задумывал сразу же перейти к подробному разбору листинга программы, который заставлял попеременно перемигиваться наши светодиоды, но уже перейдя к написанию, я вдруг осознал для себя, что есть большое количество вопросов без ответа на которые — перейти к рассмотрению программы было бы преждевременно. И для себя я определил целый перечень таких вопросов :
Именно с рассмотрения этих вопросов я хотел бы продолжить повествование о программировании STM32.
Основные логические операции
Только начиная изучать микроконтроллеры, слова «регистр» и «битовые операции» для меня казались чем-то таинственно загадочным и я долго не хотел переходить к рассмотрению данной темы. Но когда я более-менее разобрался с тем, что это такое я понял что зря откладывал изучение такой важной темы в дальний ящик. Битовые операции наверное самые распространенные операции в микроконтроллере и знание того, как и зачем их можно применять в нашей работе — откроет перед нами огромный потенциал возможностей для управления всем и вся в нашем МК!
Все мы на уроках информатики в школе знакомились с тем, что такое цифровая техника, почему она так называется, какие существуют основные логические операции.Все современные цифровые технологии основаны на двоичной математике и логических схемах.
Микроконтроллер всегда оперирует только двумя состояниями: «ноль» — нет напряжения, «единица» — есть напряжение. Давайте немного освежим в голове знания о основных логических операциях т.к. они составляют основу всей цифровой техники.
Битовые операции
Битовые операции — практически то же самое, что и логические операции только лишь с той разницей, что применяются они к битам и к числам двоичной системы.
К слову говоря, для простоты изучения битовых операций я использовал программу 32-bit ASM Calculator от ManHunter. С помощью данной программы можно проверять результаты выполнения битовых операций, переводить числа из одной системы счисления в другую. Программа имеет интуитивно понятный интерфейс и после знакомства программа стала одним из основных инструментов в моей работе с микроконтроллерами. Небольшое пояснение к интерфейсу программы данно на изображении ниже:
Битовая операция «НЕ» — «
Если бит равен «1», то после выполнения операции «НЕ» он будет равен «0», и наоборот. Операция сразу же выполняется над всеми битами двоичного числа. Например, инвертируем число FF:
Битовая операция «И» — «&»
Если оба бита в разряде равны «1», то после выполнения операции «И» результат в разряде будет равен «1», но если хотя бы один из битов равен «0» тогда и результат будет равен «0». Операция так же выполняется поразрядно. Например, «умножим» два числа 0xFF0 и 0xF0F:
В результате мы увидим, что в тех разрядах где были единицы в обоих числах, в результате получились единицы, во всех остальных случаях — нули.
Рассмотрим варианты практического применения:
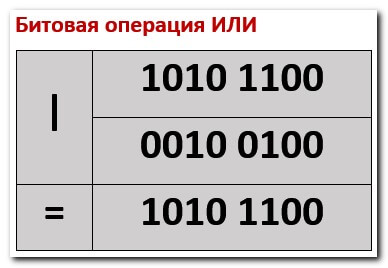
Битовая операция «ИЛИ» — «|»
Если один или оба из пары битов равен «1» то результат будет «1», иначе если оба бита равны «0» то результат будет равен «0». То есть, грубо говоря, производится сложение всех единиц в разрядах. Например если мы складываем два числа 0xF8F и 0x7F, то получим следующий результат:
Попробуйте самостоятельно поиграться с различными числами и понаблюдать за результатами.
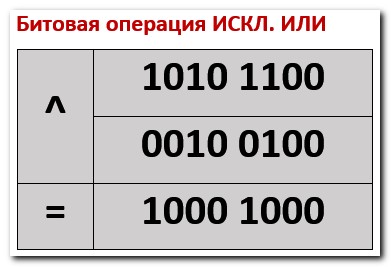
Битовая операция «ИСКЛЮЧАЮЩЕЕ ИЛИ» — «^»
Если биты в разряде отличаются и не равны тогда результат будет «1», иначе «0». Например, если мы делаем XOR числа 0xF8F и 0x7F, то мы увидим что в разрядах в которых находятся отличные биты то там в результате получается «1» и в местах где биты одинаковые, будь то «0» или «1» — получился «0», в итоге мы получим следующий результат:
Рассмотрим варианты практического применения:
Битовые операции сдвига
Существует ряд интересных и порой чрезвычайно полезных битовых операций именуемых как операции сдвига. Двигать разряды можно как вправо, так и влево. В ходе данной операции происходит сдвиг всех разрядов двоичного числа на указанное количество позиций, при этом, в случае если сдвиг идёт влево — старший бит (самый левый) теряется, а в младший (самый правый) записывается «0». При логическом сдвиге вправо происходит обратная ситуация — младший бит (самый правый) теряется, а в старший записывается «0». Дополнительно хотелось бы отметить, что в случае 32-разрядных слов сдвигаются все 32 разряда целиком. Рассмотрим операции сдвига подробнее.
То, что получается в результате сдвига вправо достаточно наглядно отражено на изображении:
При двоичном сдвиге вправо можно заметить что происходит ситуация обратная сдвигу влево — число делится на 2 с при сдвиге в 1 разряд и после на 2 * n, где n — количество разрядов на которые произведен сдвиг. Так же попробуйте самостоятельно поиграться с числами и которые заведомо делятся на 2 нацело. И вопрос на засыпку — какой результат будет если вы поделите таким образом нечетное число?
Важное замечание. Если вы будете делать сдвиг для переменной с отрицательным знаком (signed) — освободившиеся позиции будут заполняться единичками.
В качестве заключения.
Многим начинающим данная тема может показаться дико скучной и может сложиться ощущение что ну вообще не понятно где и как можно применить эти знания. Спешу вас обнадежить, в ситуациях когда нужно поднять ту или иную ногу МК или записать параметр в какой-нить периферийный блок или модуль — там кругом и всюду будут требоваться знания битовых операций. Так как статья получилась достаточно объемной, рассмотрение регистров мы перенесем на следующий урок. Ну и в последующем можно использовать эту статью как шпаргалку.
В качестве домашнего задания попробуйте самостоятельно разобрать код нашей программы в блоке while(1) и понять как же битовыми операциями мы включаем и выключаем наши светодиоды. Ну а на следующем уроке я расскажу как оно происходит на самом деле!
Побитовые операторы
Побитовые операторы интерпретируют операнды как последовательность из 32 битов (нулей и единиц). Они производят операции, используя двоичное представление числа, и возвращают новую последовательность из 32 бит (число) в качестве результата.
Эта глава требует дополнительных знаний в программировании и не очень важная, при первом чтении вы можете пропустить её и вернуться потом, когда захотите понять, как побитовые операторы работают.
Формат 32-битного целого числа со знаком
Побитовые операторы в JavaScript работают с 32-битными целыми числами в их двоичном представлении.
Это представление называется «32-битное целое со знаком, старшим битом слева и дополнением до двойки».
Разберём, как устроены числа внутри подробнее, это необходимо знать для битовых операций с ними.
Что такое двоичная система счисления, вам, надеюсь, уже известно. При разборе побитовых операций мы будем обсуждать именно двоичное представление чисел, из 32 бит.
Старший бит слева – это научное название для самого обычного порядка записи цифр (от большего разряда к меньшему). При этом, если больший разряд отсутствует, то соответствующий бит равен нулю.
Примеры представления чисел в двоичной системе:
Обратите внимание, каждое число состоит ровно из 32-битов.
Дополнение до двойки – это название способа поддержки отрицательных чисел.
Например, вот число 314 :
Принцип дополнения до двойки делит все двоичные представления на два множества: если крайний-левый бит равен 0 – число положительное, если 1 – число отрицательное. Поэтому этот бит называется знаковым битом.
Список операторов
В следующей таблице перечислены все побитовые операторы. Далее операторы разобраны более подробно.
| Оператор | Использование | Описание |
|---|---|---|
| Побитовое И (AND) | a & b | Ставит 1 на бит результата, для которого соответствующие биты операндов равны 1. |
| Побитовое ИЛИ (OR) | a | b | Ставит 1 на бит результата, для которого хотя бы один из соответствующих битов операндов равен 1. |
| Побитовое исключающее ИЛИ (XOR) | a ^ b | Ставит 1 на бит результата, для которого только один из соответствующих битов операндов равен 1 (но не оба). |
| Побитовое НЕ (NOT) | Заменяет каждый бит операнда на противоположный. | |
| Левый сдвиг | a | Сдвигает двоичное представление a на b битов влево, добавляя справа нули. |
| Правый сдвиг, переносящий знак | a >> b | Сдвигает двоичное представление a на b битов вправо, отбрасывая сдвигаемые биты. |
| Правый сдвиг с заполнением нулями | a >>> b | Сдвигает двоичное представление a на b битов вправо, отбрасывая сдвигаемые биты и добавляя нули слева. |
Побитовые операторы работают следующим образом:
Посмотрим, как работают операторы, на примерах.
Для удобной работы с примерами в этой статье, если вы захотите протестировать что-то в консоли, пригодятся две функции.
Задаю этот вопрос скорее для самообразования, чем из реальной сиюминутной необходимости:
Что нужно знать программистам «более высоких уровней» о побитовых операциях? О каких конкретных случаях их применения желательно знать в любом случае? Приведите примеры из вашей практики, когда использования побитовых операций существенно ускоряло/упрощало?/улучшало ваш код?
Что я уже знаю:
Также я прочитал все топики на эту тему здесь на ХэшКоде и основные на StackOverflow, нашёл вот этот интересный ресурс: Bit Twiddling Hacks.
И наслышан о книге Hacker’s Delight, которую пока что не читал. Она же на русском.
В дополнение к вопросу напишу, что кроме битовых масок (которые я уже давно использую) из всего того, что мне встретилось, единственным более-менее полезным для себя и своей повседневной практики я нашёл лишь только проверку числа на чётность, что навело меня на мысль, что наверняка должны быть какие-то ещё диковинные случаи, когда использование битовых операций уместно и даже желательно.
И ещё напишу, что интересуюсь этим вопросом сугубо с практической стороны, поэтому скорее буду признателен за простые примеры и реальный опыт, чем за сухие ссылки на «6 том всемирного собрания алгоритмов из какого-нибудь Великого британского учебного учреждения» и всё в таком духе.
Перечень интересных ссылок на смежные темы
4 ответа 4
Ну про битовые сдвижки вы уже сами все написали, так что повторяться не буду.
А OR это просто сложение двух битовых массивов.
Update
Примерчик c битами конвертация байта в 16-тиричную строку (Java):
Битовые операции обычно нужны лишь для экстремальной оптимизации. В обычных случаях можно обходиться без них. В обычных случаях битовые трюки затрудняют понимание кода, применяйте их только если они вам осознано необходимы. Учтите, что современные компиляторы довольно умны, и применяют битовые трюки самостоятельно. Многие программисты, к сожалению, злоупотребляют низкоуровневыми оптимизациями, что вредит качеству кода: код становится очень сложным в поддержке, хрупким, и подверженным тонким ошибкам.
С другой стороны, раз уж битовые операции так часто используются, стоит их знать, чтобы уметь корректно читать и понимать чужой код.
Для работы с упакованными значениями в C (и C++), например, обычно лучше использовать не сдвиги и маски, а битовые поля. О нужных величинах сдвига позаботится сам компилятор. В C (и кажется в C++) для выделения старшего и младшего полубайта лучше использовать такую структуру:
(учтите, стандарт не даёт гарантий правильности этого, так как, например, нет гарантий, что байт содержит в точности 8 бит).
Важный частный случай, в котором нужны битовые операции — массив бит (например, вы хотите использовать реально много булевых значений, и хотите пожертвовать скоростью ради выигрыша в размере структуры данных. Для этого вы можете завести большой массив char ‘ов, и адресовать в нём биты следующим образом:
Ещё один важный частный случай — это реализация алгоритмов наподобие криптографических, которые сами оперируют с битовыми представлениями чисел. Здесь, конечно, без битовой арифметики не обойтись.
Для чего нужны битовые операции?

Здравствуйте! Еслть 4 диапазона чисел: 0-100, 0-100, 0-6000, 0-3. Сделать в виде битовых операций.

Даны числа x и y. Используя только битовые операции и операции арифметического сложения и.
Ну например битовые операции (в частности, битовый сдвиг (причем сдвигов бывает целая куча видов)) нужны для умножения/деления чисел.
Также битовые операции (в частности, операция xor) широко используются в криптографических целях.
Вобще говоря, я когда только начинал читать литературу по Си++ (или чистому Си), то тоже задавался вопросом о предназначении битовых сдвигов и других операций.
Эта тема манипулирования числами на уровне битов очень хорошо обмусоливается в учебниках по ассемблеру.
DavidTs, это типа как сложение двоичных кодов?
Добавлено через 29 секунд
Ferrari F1, если вначале не понимал для чего нужны битовые операции, потом все равно же как-то понял. Как?
все эти настройки могут сосуществовать одновременно,
и они управляют логикой работы механизма.
как можно было реализовать такое?
можно было бы например,
создать класс, и завести в нем булевые переменные на каждый возможный режим.
в итоге у вас может образоваться целая толпа булевых переменных,
из-за которых сильно разбухнет размер класса.
кроме того, как задавать все эти режимы работы?
заводить отдельный метод на каждый флажок что ли?
в одну 32 битную интовую переменную влезет до 32 различных флагов включительно.
просто представьте себе сколько булевых переменных может сэкономить одна интовая.
и работать с ними удобно:
можно указывать сразу пачку флажков через символ «палка».
деактивировать сразу пачками.
проверять по нескольку флажков за раз.
благодаря чему, при помощи флагов удобно обрабатывать сложную логику,
которая зависит от совокупности множества факторов.
по этой причине, битовые операции получили широчайшее распространение
в области разработки «машин состояний».
Битовые операции
Логические битовые (побитовые) операции
Битовые операции сдвига
В распространённых языках программирования встроенными средствами реализуются только четыре побитовые (битовые) логические операции : И, ИЛИ, НЕ и исключающее ИЛИ. Для задания произвольной побитовой логической операции вполне достаточно перечисленных операций.
И еще, регистр общего назначения (R0. R31) я буду обозначать аббревиатурой РОН.
Битовые (побитовые) логические операции
Битовая операция НЕ:
Если бит равен «1», то после выполнения операции он будет равен «0». И наоборот, если бит равен «0», то после выполнения операции он будет равен «1». (операция выполняется одновременно над всеми битами РОН). В качестве операнда может использоваться только РОН
Обозначается знаком «
Дополнительный код, как и прямой и обратный коды — наиболее распространённые способы представления десятичных чисел в двоичном коде. Это вопрос будет рассмотрен в отдельной статье.
Битовая операция И:
Если оба соответствующих бита операндов равны 1, результирующий двоичный разряд равен 1; если же хотя бы один бит из пары равен 0, результирующий двоичный разряд равен 0. В качестве операндов могут использоваться два РОН или РОН и константа (число, записанное в памяти МК)
Обозначается знаком «&»
Практическое применение:
— для сброса конкретного бита (битов) в ноль:

— для проверки бита на 0 или 1, оно же чтение конкретного бита (если результат равен 0, значит бит равен 0, иначе бит равен 1):
Битовая операция ИЛИ
Если оба соответствующих бита операндов равны 0, двоичный разряд результата равен 0; если же хотя бы один бит из пары равен 1, двоичный разряд результата равен 1. В качестве операндов могут использоваться два РОН или РОН и константа
Обозначается знаком «|» (вертикальная палочка)
Битовая операция ИСКЛЮЧАЮЩЕЕ ИЛИ
Результат действия выполнения операции равен 1, если число складываемых единичных битов нечётно и равен 0, если чётно. В качестве операндов могут использоваться только РОН
Обозначается знаком «^»
Практическое применение:
— для инвертирования битов регистра по маске
Битовые операции сдвига
Логический сдвиг влево
При логическом сдвиге влево происходит сдвиг всех разрядов регистра влево на одну позицию, старший бит (самый левый) при этом теряется, а в младший (самый правый) записывается 0.
Обозначается знаком «
Логический сдвиг вправо
При логическом сдвиге вправо происходит сдвиг всех разрядов регистра вправо на одну позицию, младший бит (самый правый) при этом теряется, а в старший (самый левый) записывается 0
Обозначается знаком «>>»
Логический сдвиг вправо используется как арифметическая операция для целочисленного деления на 2.