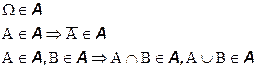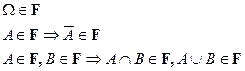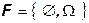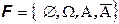зачем нужна сигма алгебра
Зачем нам нужны сигма-алгебры для определения вероятностных пространств?
Может ли кто-нибудь объяснить простым языком, почему здание вероятности рухнет, если у нас не будет σ ‘ role=»presentation»> σ алгебры? Они просто вклиниваются посередине с этим невероятно каллиграфическим «F». Я верю, что они необходимы; Я вижу, что событие отличается от результата, но что было бы неправильно без σ ‘ role=»presentation»> σ алгебры?
Вопрос в том, в каком типе вероятностных задач определение вероятностного пространства, включающего σ ‘ role=»presentation»> σ алгебру, становится необходимостью?
Этот онлайн-документ на веб-сайте Дартмутского университета дает понятное объяснение на английском языке. Идея заключается в вращающемся указателе, вращающемся против часовой стрелки на окружности единицы периметра:
К первому пункту Сианя: когда вы говорите об алгебрах, вы спрашиваете об измеримых множествах, поэтому, к сожалению, любой ответ должен быть сосредоточен на теории меры. Я постараюсь довести это до конца нежно. σ ‘ role=»presentation»> σ
Теория вероятностей, допускающая все подмножества несчетных множеств, сломает математику
Но что, если область набора интересов не является четко определенной?
Хорошая новость: алгебры строго необходимы только для несчетных множеств σ ‘ role=»presentation»> σ
Поэтому на практике достаточно просто сделать это наблюдение достаточным для того, чтобы сделать наблюдение, в котором вы рассматриваете только измеримые по Лебегу множества, чтобы добиться прогресса в решении проблемы интересов.
Но подождите, что такое неизмеримый набор?
Боюсь, я могу только пролить немного света на это сам. Но парадокс Банаха-Тарского (иногда парадокс «солнца и гороха») может нам помочь:
Для заданного сплошного шара в трехмерном пространстве существует разложение шара на конечное число непересекающихся подмножеств, которые затем можно соединить по-разному, чтобы получить две идентичные копии исходного шара. Действительно, процесс сборки включает в себя только перемещение деталей и их вращение без изменения их формы. Однако сами кусочки являются не «твердыми телами» в обычном смысле, а бесконечным рассеянием точек. Реконструкция может работать всего с пятью частями.
Более сильная форма теоремы подразумевает, что при наличии любых двух «разумных» твердых объектов (таких как маленький шар и огромный шар) любой из них может быть повторно собран в другой. Об этом часто говорят неформально: «горох можно нарезать и снова собрать в Солнце» и называют «парадоксом гороха и солнца». 1
Чтобы разрешить этот парадокс, можно сделать одну из четырех уступок:
Сигма-алгебра
σ-алгебра (си́гма-а́лгебра) — алгебра множеств, замкнутая относительно операции счётного объединения. Сигма-алгебры играют важнейшую роль в теории меры и интегралов Лебега, а также в теории вероятностей.
Содержание
Определение
Семейство 

Замечания
Связанные определения
Примеры
Полезное
Смотреть что такое «Сигма-алгебра» в других словарях:
Булева сигма-алгебра — Борелевская сигма алгебра это минимальная сигма алгебра, содержащая все открытые подмножества топологического пространства (впрочем, она содержит и все замкнутые). Если не оговорено противное, в качестве топологического пространства выступает… … Википедия
Борелевская сигма-алгебра — это минимальная сигма алгебра, содержащая все открытые подмножества топологического пространства (также она содержит и все замкнутые). Эти подмножества также называются Борелевыми. Если не оговорено противное, в качестве топологического… … Википедия
Алгебра (теория множеств) — У этого термина существуют и другие значения, см. Алгебра (значения). Алгебра множеств в теории множеств это непустая система подмножеств, замкнутая относительно операций дополнения (разности) и объединения (суммы). Содержание 1 Определение … Википедия
Алгебра (значения) — Алгебра раздел математики либо математическая структура специального вида (см. Алгебраическая система) Как раздел математики Абстрактная алгебра Алгебра логики раздел математической логики. Коммутативная алгебра Линейная алгебра… … Википедия
Алгебра множеств — У этого термина существуют и другие значения, см. Алгебра (значения). Алгебра множеств в теории множеств это непустая система подмножеств, замкнутая относительно операций дополнения (разности) и объединения (суммы). Содержание 1 Определение … Википедия
Сигма — У этого слова несколько значений: Сигма буква греческого алфавита. Сигма (язык) Стандартное отклонение в теории вероятностей. Сигма алгебра в теории множеств. «Сигма» чешский футбольный клуб. Sigma Corporation японский производитель… … Википедия
Σ-алгебра — (сигма алгебра) это алгебра множеств, замкнутая относительно операции счётного объединения. Сигма алгебры играют важнейшую роль в теории меры и интегралов Лебега, а также в теории вероятностей. Содержание 1 Определение 2 Замечания 3 … Википедия
Борелевская алгебра — Борелевская сигма алгебра это минимальная сигма алгебра, содержащая все открытые подмножества топологического пространства (впрочем, она содержит и все замкнутые). Если не оговорено противное, в качестве топологического пространства выступает… … Википедия
Измеримое пространство — σ алгебра (сигма алгебра) это алгебра множеств, замкнутая относительно операции счётного объединения. Сигма алгебры играют важнейшую роль в теории меры и интегралов Лебега, а также в теории вероятностей. Содержание 1 Определение 2 Замечания 3 … Википедия
Алгебра и сигма-алгебра



При построении математической модели случайного объекта необходимо не только указать все возможные элементарные исходы опыта, но и определить (перечислить) все возможные события, которые могут произойти в этом опыте. Принято следующее определение:
Алгебра событийAэто набор подмножеств пространства элементарных исходов 
и для любой счетной последовательности
Очевидно, что любая сигма-алгебра является алгеброй, но не наоборот.
Колмогоров показал, что естественной математической моделью для множества событий является сигма-алгебра.
Очевидным примером сигма-алгебры является набор всех подмножеств пространства элементарных исходов – это наибольшая сигма-алгебра, возможная на данном пространстве элементарных исходов.
Наименьшая (тривиальная) сигма-алгебра это следующий набор подмножеств
Алгебры и сигма-алгебры обозначаем жирными наклонными латинскими буквами.
Глава 6 Решение задач по теме Сигма-алгебра
Конспект: Алиса Жильцова
дата: 30 сентября 2016 г.
6.1 Задача №1 (№ 2.35 в задачнике)
6.1.1 Условие задачи:
Приведите по два нетривиальных (т.е. \(\Omega\) и \(\emptyset\) не называть) примера такого события A, что:
Упростите выражения: \(\mathcal
6.1.2 Решение:
Приведём по два нетривиальных (т.е. \(\Omega\) и \(\emptyset\) не называть) примера такого события A, что:
Начнём с того, что \(\mathcal
\(\bullet\) A лежит в каждой \(\mathcal
Попробуем привести другой пример события, лежащего во всех \(\mathcal
Событие \(X_ <37>> 0\) означает, что в 37-м подбрасывании выпал орёл. Оно входит во все \(\mathcal
А этот пример еще интереснее! В нем есть ловушка! 🙂
Упростим следующие выражения:
Аналогично предыдущим пунктам получим: \(\mathcal
6.2 Задача №2 Про Агента 007 (№ 2.43 в задачнике)
6.2.1 Условие задачи
Сейчас либо солнечно, либо дождь, либо пасмурно без дождя. Соответственно множество \(\Omega\) состоит из трёх исходов, \(\Omega\) = <солнечно, дождь, пасмурно>. Джеймс Бонд пойман и привязан к стулу с завязанными глазами, но он может на слух отличать, идет ли дождь.
6.2.2 Решение задачи
Введём случайную величину Z, означающую то, что различает Джеймс Бонд. Другими словами, зная Z Джеймс Бонд с легкостью сможет сказать, идёт сейчас дождь или нет. Но он не отличает события <солнечно>и <пасмурно>.
Оформим возможные значения Z в виде таблицы:
| \(\Omega\) | Солнечно | Дождь | Пасмурно |
|---|---|---|---|
| Z | 0 | 1 | 0 |
На бытовом языке такую сигма-алгебру можем описать как список событий, который различает Джеймс Бонд, если бы ему завязали глаза и заткнули бы уши (печально!), т.е. если бы он не знал ничего.
Изобразим такие сигма-алгебры графически:
Ответ: таких сигма-алгебр существует всего 5!
6.3 Задача №3 (2.39 в задачнике)
6.3.1 Условие задачи (перевод)
6.3.2 Решение задачи
Прежде чем приступить к решению следует сразу разобраться в условии задачи. Выделим некоторые ключевые моменты, необходимые для понимания:
\(\bullet\) Первый момент не может являться локальным максимумом. В нашей последовательности \(X_0\) отсутствует, а значит, первый момент не берется в рассмотрение!
\(\bullet\) Для того, чтобы лучше понять, что же такое T, приведем пример с помощью картинки для последовательности (+1,+1,-1,-1,+1,-1):
На графике видим, что вторым локальным максимумом является точка (5,1), а момент T равен 6.
Интуитивно это можно представить так: Джон играет с ребятами, а в момент времени Т его зовёт бабушка Йоко. Что знает Джон? Он знает всё, что было до момента времени Т включительно, а что было после, он уже не видел. Что он может знать? Он знает, чему равно T.
Теперь, детально разобрав условие задачи, ответим на следующие вопросы.
\(\mathcal
Сигма-алгебры
Для просмотра формул ваш браузер должен поддерживать MathML.
| Объявления | Последний пост | |
|---|---|---|
 | Работодателям и кадровым агентствам: Размещение вакансий | 26.03.2008 03:07 |
 | Математики, программисты, репетиторов (платформа SapioX) | 28.01.2021 12:47 |
 | Работа автором топиков и проектов на математическом треке Hyperskill | 24.09.2021 21:18 |
Читаю стохастический анализ и натолкнулся на определение сигма-алгебры. Для начала, что я понял.
Вероятности событий из порожденной сигма-алгебры вычисляются однозначно по вероятностям событий, эту сигма-алгебру порождающих. Так что ваш вопрос можно переформулировать так: «зачем знать, когда можно не знать?»
Во-первых, большое спасибо! Во-вторых, я как раз и пытаюсь осмыслить все эти понятия.
Я правильно понимаю, что сигма алгебра даёт нам возможность измерить любую счётную комбинацию интревалов на R по мере P? То есть, если нам дано интересное множество в R мы придумываем метод его построения из счётного множества интревалов на R. Для любого из этих «элементарных» интервалов мы можем найти прообраз в сигма-алгебре, а значит можем измерить его. Иными словами сигма алгебра даёт нам возможность построить функцию из борелевой алгебры в [0, 1]?
Можно ли привести паталогический случай, где незамкнутость множества событий помешала бы нам найти решение практической задачи? Ещё раз спасибо.
Патологических примеров вам разбирать не нужно. Они имеют чисто теоретическое значение, слишком сложны и неестественны. Поймите сначала то, что просто и нужно.