зачем нужна последовательность фибоначчи
Число Фибоначчи. Почему оно так популярно в природе?
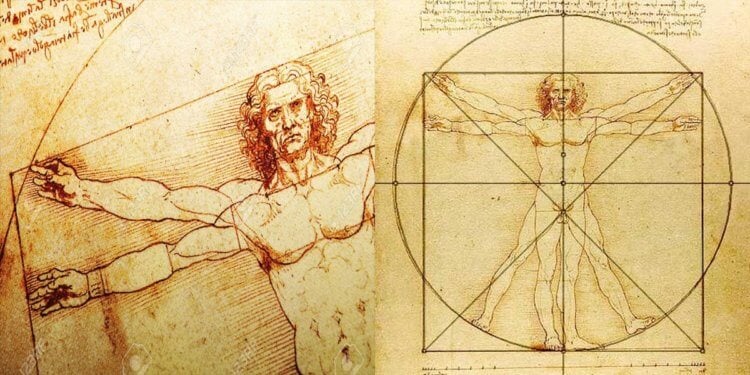
Таинственное число Фибоначчи, равное 1,618, будоражит умы ученых уже на протяжении нескольких тысячелетий. Кто-то считает это число строителем мироздания, кто-то называет его числом Бога, а кто-то, не мудрствуя лукаво, просто применяет его на практике и получает невероятные архитектурные, художественные и математические творения. Число Фибоначчи было обнаружено даже в пропорциях знаменитого «Витрувианского человека» Леонардо Да Винчи, который утверждал, что знаменитое число, пришедшее из математики, руководит всей Вселенной.
«Витрувианский человек» Леонардо да Винчи обладает идеальными пропорциями, основанными на знании свойств числа Фибоначчи
Кто такой Фибоначчи?
Леонардо Пизанский считается самым первым крупным математиком в истории средневековой Европы. Несмотря на это, свое знаменитое прозвище «Фибоначчи» ученый получил далеко не из-за своих экстраординарных математических способностей, но из-за своего везения, так как «боначчи» по-итальянски означает «удачливый». Перед тем как стать одним из самых известных математиков раннего Средневековья, Леонардо Пизанский изучал точные науки у самых продвинутых учителей своего времени, которыми считались арабы. Именно благодаря этой деятельности Фибоначчи, в Европе появились десятичная система счисления и арабские цифры, которыми мы пользуемся до сих пор.
В одном из своих самых известных трудов под названием «Liber abaci», Леонардо Пизанский приводит уникальную закономерность чисел, которые при постановке в ряд образуют линию цифр, каждая из которых является суммой двух предыдущих чисел.
Последовательность Фибоначчи
Иными словами, последовательность Фибоначчи выглядит так:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 и так далее.
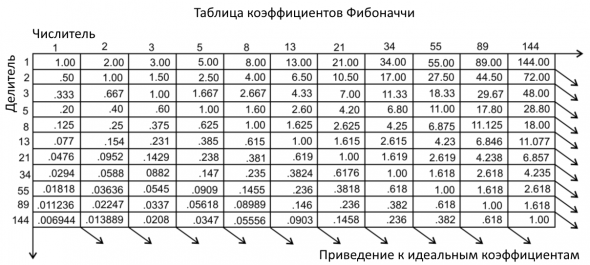
Каждое число из ряда Фибоначчи, разделенное на последующее, имеет значение, стремящееся к уникальному показателю, которое составляет 1,618. Первые числа ряда Фибоначчи не дают настолько точное значение, однако по мере нарастания, соотношение постепенно выравнивается и становится все более точным.
Леонардо Пизанский — тот самый создатель числа Фибоначчи
Где используется число Фибоначчи
Из-за своего повсеместного применения в природе, золотое сечение (именно так число Фибоначчи иногда называют в искусстве и математике) считается одним из самых гармонизирующих законов мироздания, который упорядочивает структуру окружающего нас мира и направляет жизнь на развитие. Так, правило золотого сечения применяется природой для образования траекторий движения вихревых потоков в ураганах, при образовании эллиптических галактик, к которым относится и наш Млечный Путь, при «строительстве» раковины улитки или ушной раковины человека, направляет движение косяка рыб и показывает траекторию движения испуганной стаи оленей, врассыпную убегающую от хищника.
Проявление золотого сечения в природе
Эстетичность такой гармонизации мироздания воспринимается человеком, который всегда стремился улучшить окружающую его действительность, в качестве стабилизирующего природу закона. Находя золотое сечение в лице того или иного человека, мы инстинктивно воспринимаем собеседника в качестве гармоничной личности, чье развитие происходит без сбоев и нарушений. Этим можно объяснить то, почему иногда нам по непонятным причинам больше нравится одно лицо, чем другое. Оказывается, о наших возможных симпатиях позаботилась природа!
Как вы считаете, является ли повсеместное применение числа Фибоначчи в природе совпадением или свидетельством наличия некоего вселенского разума? Давайте попробуем обсудить этот вопрос в нашем Telegram-чате.
Наиболее распространенное определение золотого сечения гласит, что меньшая часть так относится к большей, как большая часть относится ко всему целому. Уникальное правило встречается во всех областях природы, науки и искусства, позволив некоторым именитым исследователям Средних Веков сделать предположение, что три основные части золотого сечения олицетворяют собой христианских Отца, Сына и Святого Духа.
Правилу золотого сечения следуют даже галактики. Наш Млечный Путь в этом плане не является исключением
Что такое золотое сечение
С точки зрения математики, золотое сечение представляет собой некую идеальную пропорцию, к которой каким-то образом стремится все живое и неживое в природе.
Так выглядит «золотое сечение»
Используя основные принципы ряда Фибоначчи, растут семечки в центре подсолнуха, движется спираль ДНК, был построен Парфенон и написана самая знаменитая картина в мире — «Джоконда» Леонардо Да Винчи.
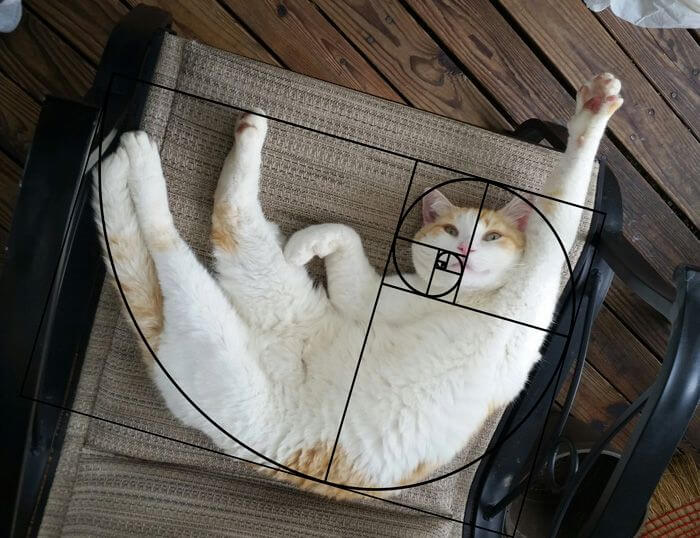
Даже коты неосознанно (хотя, кто знает?) следуют принципу золотого сечения, становясь любимцами большей части населения планеты
Есть ли в природе гармония? Несомненно, есть. А ее доказательством служит число Фибоначчи, происхождение которого нам еще только предстоит отыскать.
Новости, статьи и анонсы публикаций
Свободное общение и обсуждение материалов
Ученые обнаружили, что на границе между Землей и космосом могут возникать ураганы. 🌀 Это очень красивое явление, которое сопровождается ярким полярным сиянием. Рассказываем, как образуются обычные ураганы и каким образом ураган возник в таком необычном месте.
В июле 2020 года в зарубежных СМИ появились тревожные сообщения о том, что на территории южноафриканской страны Ботсвана начали массово гибнуть слоны. Местны…
Происхождение и применение последовательности Фибоначчи
От Фибоначчи до Эллиотта
Автор: Джеффри Кеннеди
Вы скажете, что это ещё одно модное или «умное» словечко, которое чаще используют, чтобы произвести впечатление, чем чтобы объяснить. Несколько лет назад модным словечком, которое я слышал чаще всего, было «беспроигрышный» — концепция, популяризированная Стивеном Кови. К сожалению, в последние годы технические аналитики подняли «Фибоначчи» на тот же уровень. Понимание этого термина, возможно не спасёт его от статуса «умного слова», но даст некоторое представление о причинах его популярности.
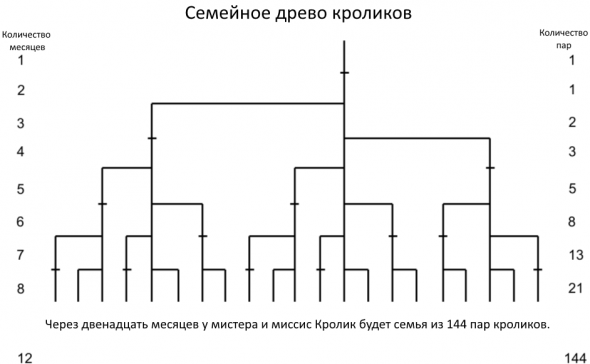
Леонардо Пизанский Фибоначчи был математиком в тринадцатом веке, который задал вопрос: сколько пар кроликов может появиться от одной пары в закрытой среде за год, если каждая крольчиха рождает пару крольчат каждый месяц, а способность к производству потомства у них появляется по достижению двухмесячного возраста? Ответ: 144.
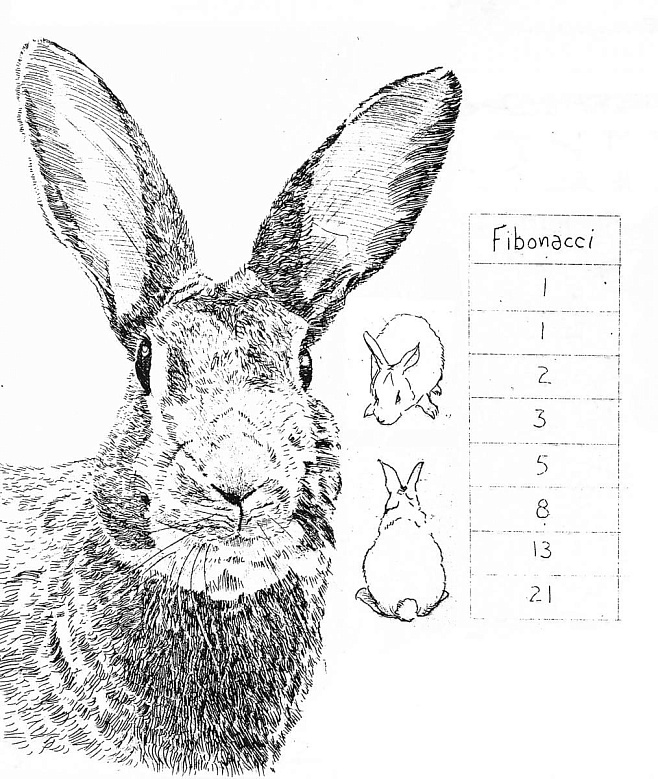
Гениальность этого простого маленького вопроса не в ответе, а в последовательности чисел, с помощью которой был найден ответ: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 и 144. Эта последовательность чисел представляет собой увеличение популяции кроликов в течение 12-месячного периода и называется последовательностью Фибоначчи.
Поскольку Леонардо Фибоначчи изначально изучал размножение наших маленьких пушистых друзей, актуальность этого соотношения была доказана снова и снова. Во всём, от цепочки ДНК до галактики в которой мы живём присутствуют уровни Фибоначчи, они определяют естественный прогресс роста и распада. Простым примером является человеческая рука, состоящая из пяти пальцев, каждый из которых состоит из трёх костей.
Помимо открытия того, что фондовый рынок состоит из волн, образующих повторяющиеся паттерны, Р. Н. Эллиотт также осознал важность уровней Фибоначчи. В последней книге «Закон природы» он особенно подчёркивал последовательность Фибоначчи как математическую основу Волнового Принципа. Благодаря его открытиям мы используем уровни Фибоначчи при вычислении коррекции волн и проекций.
Мы также переводим непубличные статьи из MyEWI, где публикуется более детальная информация. Подписывайтесь>>>
Числа Фибоначчи: что, как и почему
Отец Фибоначчи желал, чтобы его сын, как и он сам, стал торговцем. Но, к счастью для науки, Леонардо пошел другим путем. Сейчас мы знаем Фибоначчи в первую очередь по последовательности чисел, опубликованной им в его первом трактате Liber аbaci. Но в нем есть кое-что гораздо более значимое для современной западной науки – в этой книге Фибоначчи один из первых описал использование системы счисления с индийскими цифрами. Значимость последующего перехода к индийской позиционной системе сложно переоценить – большая часть современных открытий базируется на математических расчетах, многие из которых весьма затруднительны в римской системе счисления. В качестве примера можно рассмотреть простейшие арифметические действия – умножение и деление. В привычной нам системе счисления все просто – нужно всего лишь вспомнить таблицу умножения и переносить числа из одного разряда в другой. Но в случае с римской системой такой фокус уже не сработает – если с умножением еще как-то можно справиться, то представить себе деление числа DCXXXVI на число LIII уже гораздо сложнее. Другой пример – это вся современная вычислительная техника, использующая в основном двоичную позиционную систему счисления.
Поскольку деление было очень сложным действием в римской системе счисления, для этого использовали специальный инструмент – абак
Однако вернемся к числам Фибоначчи. Несмотря на решение стать ученым, Леонардо так и не забыл того, что изначально должен был стать торговцем. Может быть, поэтому юный математик включил в свой трактат множество практических примеров, особенно полезных именно для купцов и продавцов. В частности, Фибоначчи неоднократно демонстрировал, как использование индийской системы счисления и дробей позволяет упростить и ускорить частую задачу для торговцев того времени – перевод всевозможных единиц измерения в привычные купцам единицы и валюты. С другой стороны, Леонардо Пизанский уделил значительную часть своей книги и более отвлеченным задачам – именно так и была выявлена последовательность чисел Фибоначчи.
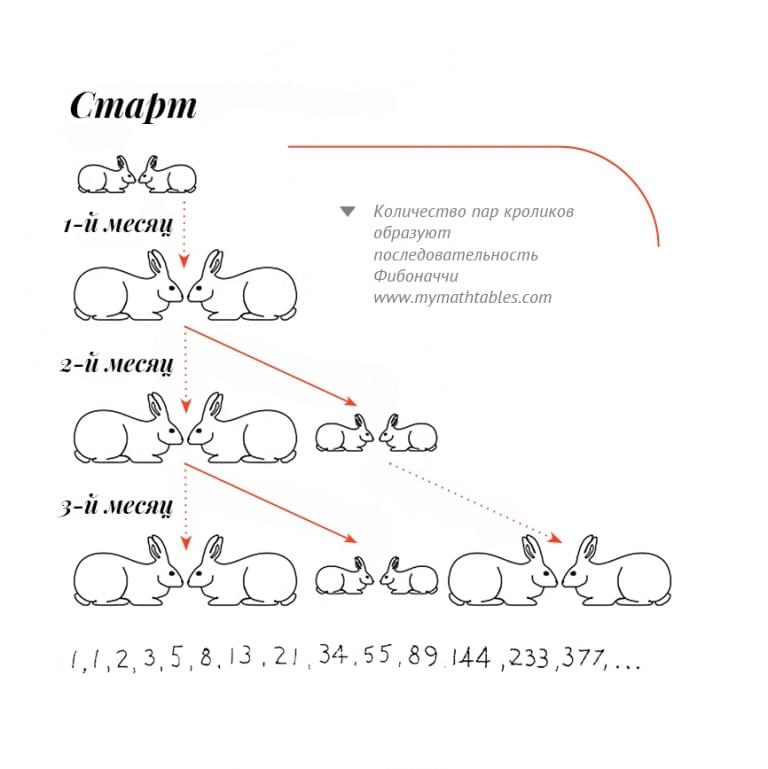
Одна из задач, поставленных математиком, звучала так: если любая пара кроликов производит новую пару каждый месяц, начиная со второго месяца существования, то сколько пар кроликов мы получим через год? При этом считается, что в начале у нас есть одна такая пара кроликов, и животные не умирают. Рассмотрим для примера первые несколько месяцев развития популяции таких кроликов.
Итак, мы начинаем с одной пары кроликов. В конце первого месяца у нас все еще одна пара. В конце второго месяца у нас есть стартовая пара кроликов и еще одна пара, родившаяся у них. К концу третьего месяца изначальная пара кроликов производит еще одну пару – в итоге мы имеем уже три пары кроликов. На этом шаге мы можем получить формулу для количества пар кроликов к концу следующего месяца – оно будет равно количеству пар в конце текущего месяца плюс их количество в конце предыдущего месяца. Зная эту формулу, мы легко можем вычислить количество пар кроликов к концу каждого месяца и получить последовательность Фибоначчи, как это сделал в свое время Леонард Пизанский. Вот искомая последовательность: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, … Однако легко заметить, что данный пример имеет мало общего с реальностью – как минимум кролики все-таки не бессмертны. Но есть и другие, гораздо более реалистичные случаи применения последовательности Фибоначчи в природе: родословная пчел, раковины моллюсков, соцветия растений, ДНК человека.
Главное, что нужно уяснить из задачи о кроликах: числа Фибоначчи – это числовая последовательность, в которой каждое новое число равняется сумме двух предыдущих. А как она применяется на практике?
Числа Фибоначчи и золотое сечение
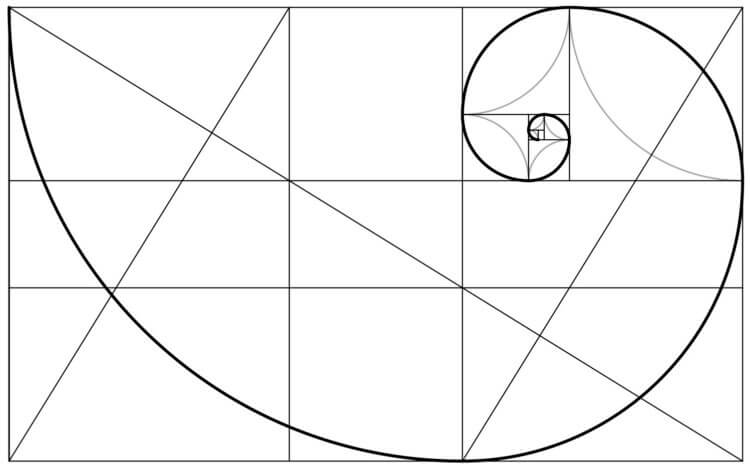
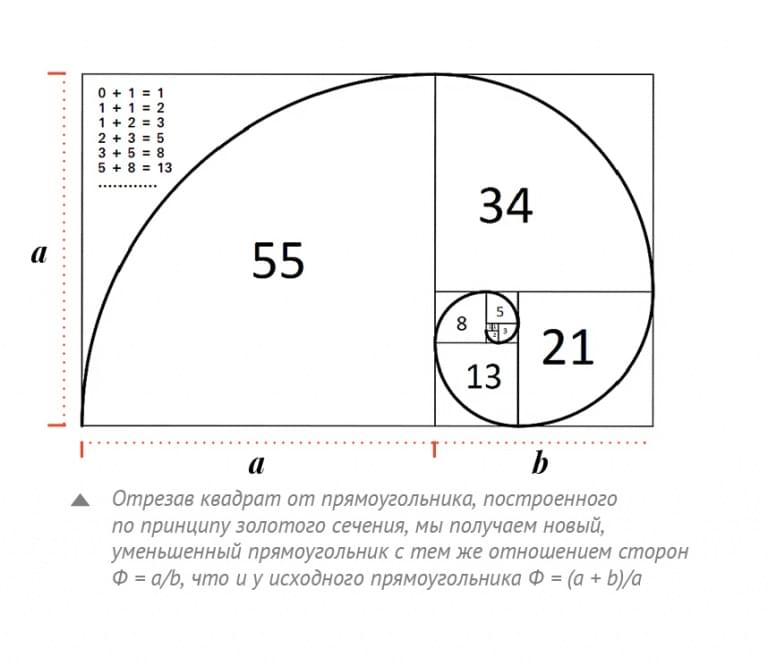
В математике на основе последовательности Фибоначчи можно построить набор квадратов со сторонами, равными элементам этой последовательности. Добавляя каждый квадрат из этого набора к сторонам двух предыдущих квадратов, мы всегда будем получать прямоугольник, стороны которого равны двум последующим числам Фибоначчи. И, наконец, если мы решим вписать в каждый из этих квадратов по четверти окружности, то мы получим аппроксимацию широко известной золотой спирали, используемой в архитектуре. На первый взгляд это описание может показаться сложным, но если взглянуть на рисунок, все сразу встает на свои места.
В этом примере наиболее ясно видна связь последовательности Фибоначчи и золотого сечения, которое используется для построения золотой спирали. Но существует и еще более явная взаимосвязь между числами Фибоначчи и золотым сечением – последнее можно напрямую получить из соотношения двух чисел Фибоначчи! Как известно, золотое сечение – это иррациональное число (то есть его нельзя выразить рациональными дробями – говоря более простым языком, это число с бесконечным числом знаков после запятой), приблизительно равное 1,618. А теперь попробуем делить каждое следующее число Фибоначчи на предыдущее, начиная с единицы: 1/1 = 1; 2/1 = 2; 3/2 = 1,5; 5/3 ≈ 1,666; 8/5 = 1,6; 13/8 = 1,625. Продолжая такие вычисления, мы будем все ближе и ближе приближаться к реальному значению золотого сечения!
Последовательности на базе чисел Фибоначчи
За века изучения чисел Фибоначчи ученые придумали множество вариаций классической последовательности. Например, зная формулу для чисел Фибоначчи, можно посчитать числа, которые должны предшествовать единице, тогда мы получим последовательность Фибоначчи с отрицательными членами:
…, –8, 5, –3, 2, –1, 1, 0, 1, 1, 2, 3, 5, …
Другой способ модифицировать последовательность Фибоначчи – складывать для получения следующего члена не два предыдущих, а три, четыре или еще больше элементов. В случае трех членов последовательность будет называться числами трибоначчи и иметь следующий вид:
0, 0, 1, 1, 2, 4, 7, 13, 24, 44, …
В итоге многовековых исследований числа Фибоначчи и полученные из них последовательности стали одними из самых изученных в теории чисел. Неудивительно, что помимо вышеприведенных примеров существует огромное количество практических применений чисел Фибоначчи.
«Случайные» числа Фибоначчи
Один из самых необычных примеров использования чисел Фибоначчи в современной математике и информатике – генерация псевдослучайных чисел. Для исследователей во всех областях наук последнее время очень важным является вопрос о случайных числах. Но что же такое случайное число?

Не вдаваясь в сложные математические выкладки, можно понять это на простом примере. Предположим, вам надо сделать выбор между двумя блюдами – например, гречкой и макаронами. При этом каких-либо явных предпочтений у вас нет. Очевидное решение – бросить монетку и решить, что будет соответствовать орлу, а что – решке. Если же вы скажете, что орел – это единица, а решка – ноль, то при помощи подбрасывания монетки сможете получить некое число. Именно число, поставленное в соответствие некому исходу события, и будет являться случайным числом, или, если говорить более научно, случайной величиной. Другой пример получения случайной величины – это бросание кости, у которой каждый результат соответствует числу от 1 до 6.
На первый взгляд действительно кажется, что для получения случайного числа достаточно всего лишь бросить монетку или игральную кость N число раз. До изобретения компьютеров люди зачастую обходились именно таким методом. Но с появлением первых вычислительных машин и усложнением научных задач ученым во всех областях науки требовались все большие и большие количества случайных чисел. Наиболее важны эти числа оказались для специалистов в области численного моделирования и оптимизации – именно для их экспериментов в первую очередь требовались огромные массивы случайных чисел. Косвенным примером важности и необходимости этих чисел служит очень популярная в XX веке книга A Million Random Digits with 100,000 Normal Deviates американского аналитического центра RAND, которая издавалась на протяжении полувека. Ее основным содержанием был миллион случайных чисел, записанных по 2500 чисел на страницу.

Возвращаясь от важности случайных чисел в науке к числам Фибоначчи, стоит отметить, что современный компьютер сам по себе не способен генерировать случайные числа. Поэтому для вычислений ученые придумали такую вещь, как генератор псевдослучайных чисел. Не вдаваясь в технические подробности, можно сказать, что практически все случайные числа, используемые сегодня в науке и в обычной жизни, являются на самом деле псевдослучайными. Это значит, что на самом деле они строятся по некоторому алгоритму и даже повторяются с определенным периодом. Если принять во внимание то, что при помощи таких псевдослучайных чисел зачастую генерируются пароли и ключи шифрования, то легко понять, насколько важна надежность этих генераторов. На практике наиболее важен период генератора – количество чисел, после которого генератор начинает генерировать ту же последовательность заново. И именно в этой области пригодились уже знакомые нам числа Фибоначчи! В 50-х годах XX века американские ученые предложили метод генерации псевдослучайных чисел на основе последовательности Фибоначчи, а в дальнейшем это изобретение привело к появлению целого семейства генераторов, которые используются и по сей день.
Таким образом небольшая задача итальянского средневекового ученого Леонардо Пизанского оказала огромное влияние на последующее развитие математики и даже затмила гораздо более важное его предложение об использовании индийской системы счисления. Сейчас нас окружает огромное количество предметов и изобретений, которые базируются на решении этой небольшой задачи, а медоносные пчелы и генераторы псевдослучайных чисел – лишь часть вселенной Фибоначчи.
Где используется последовательность Фибоначчи?
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,….
Происхождение этой последовательности обычно связывается с именем итальянского купца Леонардо Пизанского, более известного под прозвищем Фибоначчи. Он был великим математиком своего времени и его роль в развитии математики трудно переоценить. По его трудам, превосходящим арабские и средневековые европейские сочинения, учили математику до XVI-XVII веков.
Фибоначчи как бы напомнил человечеству то, что было известно ему еще с древнейших времен, как «золотое сечение». Геометрический смысл этой пропорции, заключается в таком делении отрезка, когда он весь относится к его большей части, как самая большая часть относится к меньшей. Значение золотого сечения иррационально, то есть оно не может быть вычислено абсолютно точно. Однако его можно приблизительно получить, разделив два соседних числа в ряде Фибоначчи, причем, чем больше величины чисел, тем точнее будет результат. Деление большего числа на меньшее дает значение Ф*=1.618…., а разделив меньшее на большее приблизительно получим Ф=0.618….
По дошедшим до нас памятникам архитектуры и образцам материальной культуры далеких эпох можно предположить о знании древними этих соотношений. Хотя обычно считается, что понятие золотого сечения ввел Пифагор (VI в. до н.э), но вполне возможно, что это знание более древнее и он позаимствовал эти знания у египтян или вавилонян. Пропорции пирамиды Хеопса, храмов, барельефов того времени, некоторых предметов быта и украшений, из гробницы Тутанхамона соответствуют соотношениям золотого сечения. Французский архитектор Ле Kорбюзье нашел эти соответствия в пропорциях на рельефах изображающих фараонов, они присутствуют в фасаде храмового комплекса Парфенона. На древних рельефах из египетских гробниц люди держат в руках измерительные инструменты, в которых зафиксированы эти замечательные пропорции.
О золотом сечении знал Платон (IV в до н.э), это отношение упоминается в «Началах» Евклида. После Евклида подобными исследованиями занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др. В средневековой Европе с ним познакомились по арабским переводам «Начал» Евклида. Переводчик Дж.Kампано из Наварры (III в.) сделал к переводу комментарии. Надо отметить, что в то время эти знания были тайными, тщательно оберегались от непосвященных и хранились в строгой тайне.
Золотое сечение встречается не только в искусстве и архитектуре, но и в природе. Пропорции ряда Фибоначчи присутствуют в расположении листьев на деревьях, различных семян, в биоритмах и функционировании головного мозга и зрительного восприятия, музыкальных тонах, стихотворных размерах, в генных структурах живых организмов и тому подобное.
В качестве причин, объясняющих эти явления обычно приводятся результаты исследований показавших, что наиболее устойчивые природные и социальные конфигурации имеют Фибоначчи-подобную форму, так как являются оптимальными в смысле энергетики и экономии ресурсов.
При этом совершенно не важно, что движет политиками: великие идеи, личные амбиции, интересы поддерживающих их финансово-промышленных групп или определенных групп населения, либо просто, собственная корысть. Важно то, что они, проявляя свою активность, создают политические партии, продвигают некие проекты, реализуемые в законотворческой или иной деятельности. Здесь мы имеем тот же парадокс рыночной экономики. В том случае, если деятельность политиков происходит в правовом поле, независимо от мотивации она объективно полезна обществу, так как своей суетой и мельтешением эти «брокеры политического рынка» решают задачи саморегуляции общественного организма. Продолжая аналогии можно сказать, что «трейдерами и инвесторами политического рынка» можно считать те силы, которые финансируют политическую деятельность.
Суть подхода Эллиота сводится к тому, что общество развивается и изменяется в виде распознаваемых моделей. Он выделил более десятка типов моделей движения («волн»), которые возникают в потоке рыночных цен, повторяющихся по форме, но не обязательно по времени или амплитуде. Им были даны названия, определения и иллюстрация этих моделей.
Некоторые авторы пытаются применить волновой закон Эллиота даже для анализа истории человечества, его глобального развития. Не ставя перед собой столь масштабных задач, попробуем рассмотреть с позиций применимости последовательности Фибоначчи для анализа длительности некоторых процессов, происходивших в России в XX веке, и даже попытаемся дать некий прогноз на первые десятилетия века XXI.
Необходимо отметить, что если для фондового рынка сегодня разработаны и широко используются разнообразные индексы (Доу-Джонса, NASDAQ и др.), что позволяет строить и анализировать графики их изменения во времени. Для рынка политического, такие показатели, возможно, еще предстоит создать в будущем. Интуитивно понятно, что эти гипотетические аналоги индекса Доу-Джонса должны иметь вероятностную, энтропийную природу.