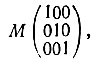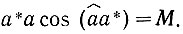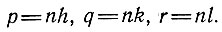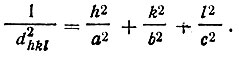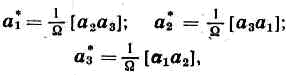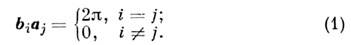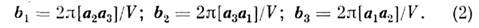зачем нужна обратная решетка

Обратная решетка

При исследовании и описании кристаллических структур часто приходится иметь дело не только с межатомными расстояниями (периодами идентичности), но и с межплоскостными расстояниями. Под межплоскостным расстоянием понимают кратчайшее расстояние между двумя соседними параллельными плоскостями данного семейства параллельных плоскостей. Для нахождения этих расстояний вводится понятие обратной решетки, которая определенным образом связана с прямой решеткой.

Обратная решетка была впервые предложена Эвальдом и была использована Лауэ для описания взаимосвязи между кристаллической структурой и дифракционной картиной. Обратная решетка не является решеткой в том обычном смысле, который мы вкладываем при определении пространственной решетки кристалла.

По Эвальду базисные вектора обратной решетки определяются соотношениями:

; ; , (6.16)

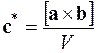
где a, b, c – базисные вектора прямой решетки; V =a[b´c] – объем элементарной ячейки прямой решетки.

Угловые параметры прямой и обратной решетки связаны соотношениями

; (6.17)

; (6.18)

. (6.19)

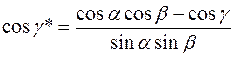
Скалярные произведения базисных векторов прямой и обратной решеток равны

(а*×а) = (b*×b) = (с*×с) = 1, (а*×b) = (а*×с) = (b*×с) = (b*×а) =

= (с*×b) = (с*×а) = 0. (6.20)

Узлы прямой и обратной решеток определяются векторами

R = ha + kb + lc, (6.21)

где h, k, l и H=nh, K=nk, L=nl – целые числа; n – общий множитель.

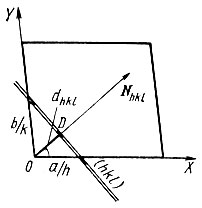
Вектор обратной решетки G = ha * + kb * + lc * перпендикулярен плоскости (hkl) прямой решетки, а длина этого вектора равна обратной величине расстояния d между плоскостями <hkl> прямой решетки, т.е.

Объем V* элементарной ячейки обратной решетки равен обратной величине объема V элементарной ячейки прямой решетки (и обратно):

Источник

5. Обратная решётка. Зоны Бриллюэна

Найдем для основных векто­ров трансляции ,,такие три вектора,,, которые обладают следующим свойством: скалярное произведение вектора на вектор (i, j = 1,2,3) равно Таким свойством обладают векторы:,,. Размерность векторов,, — обратная длина, т.е. эти векторы заданы в так называемом обратном пространстве.

Обратное пространство и обратная решетка не являются отвлечен­ными абстрактными понятиями, они имеют вполне реальное физиче­ское содержание и играют фундаментальную роль при анализе волно­вых процессов в кристаллах. Дело в том, что волновые векторы любых волн, распространяющихся в кристаллах, задаются в обратном пространстве. При этом каждому вектору обратной решетки соответствует волна с периодом, равным некоторому вектору трансляции прямой решетки.

Полученный вывод сделан для простой кубической решетки. Но он остается справедливым и для других решеток.

Источник

Зачем нужна обратная решетка

В физике твердого тела при анализе многих явлений (дифракция, движение электронов в потенциальном поле, рассеяние фотонов), связанных с периодическим расположением частиц, важную и полезную роль играет обратная решетка.

Обратная решетка представляет собой удобную абстракцию, позволяющую математически просто описать условия протекания того или иного явления в твердом кристаллическом теле.

Между векторами элементарных трансляций и параметрами обратной решетки существует вполне определенная связь.

В векторном виде эти условия записываются тремя скалярными произведениями:

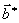
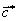
Два других вектора и определяют, исходя из сеток на других координатных плоскостях:

Рис. 1.14. К выводу связи между параметрами прямой и обратной решеток

откуда в соответствии с соотношениями (1.1), (1.2) и (1.3)

Объем элементарной ячейки обратной решетки равен

Таким образом, объем элементарной ячейки обратной решетки 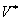есть величина обратная объему элементарной ячейки ристалла. Это соотношение является общим и применимо ко всем кристаллическим решеткам, в том числе и к непрямоугольным.

Итак, прямая и обратная ячейки взаимно сопряжены. Если для описания кристаллической решетки вместо принятой вначале выбрать другую элементарную ячейку, то для обратной решетки получится также другая группа из трех векторов, но решетка, построенная таким образом, будет идентична первой. Это следует из прямой связи между любым вектором одной решетки с одним только семейством плоскостей другой вне зависимости от координатных осей. Соответствие между двумя решетками, их взаимосвязь не зависят от выбора элементарной ячейки.

Решетка, обратная обратной решетке, является исходной (прямой) решеткой.

Каждый узел [[ HKL ]] * обратной решетки соответствует семейству параллельных плоскостей ( HKL ) прямой решетки.

Источник

Зачем нужна обратная решетка

§ 3. Обратная решетка

В частности, к этому средству приходится прибегать и в структурной кристаллографии.

Осевые орты взаимной системы a*,b*, c* определяются через осевые векторы кристаллографической системы a, b, c единичной матрицей скалярных произведений:

Геометрический смысл соотношений (5) и (6) очень прост.

Соотношение (a*a)=М означает, что
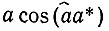
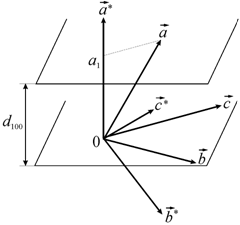
. Но -это межплоскостное расстояние между параллельными гранями YZ элементарной ячейки, т. е. межплоскостное расстояние d₁₀₀ (рис. 3, а). Следовательно, длина осевого вектора обратной решетки равна

По своей длине осевые орты a*, b*, c* обратны межплоскостным расстояниям серии плоскостей (100),(010) и (001) соответственно (с масштабным коэффициентом М).

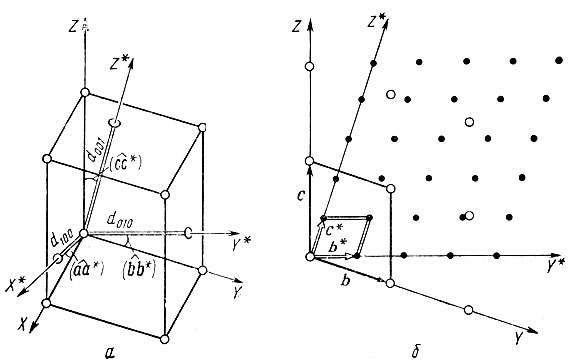
Рис. 3. Направление осей обратной координатной системы (а); построение обратной решетки (б)

Используем осевые орты а*, b*, c* для построения второй решетки, т. е. введем систему точек ·hkl·*, удовлетворяющих условию

Решетку, построенную таким образом, называют обратной по отношению к кристаллографической. Этот вспомогательный геометрический образ широко используется в рентгеноструктурном анализе для интерпретации рентгенограмм.

На рис. 4, а изображены прямая и обратная решетки (условно взяты двумерные решетки; третий индекс каждого узла можно считать равным нулю). В обратной решетке проведен узловой ряд через точки ·110·*, ·220·*, ·330·*, т. е. узловой ряд [110]*. На том же рисунке показана серия плоскостей основной решетки, имеющая те же индексы (110). Как видно, они взаимно перпендикулярны. На рис. 4, б то же построение относится к узловому ряду [310]* обратной решетки и серии узловых сеток (310) основной решетки. Узловой ряд [310]* снова перпендикулярен плоскости (310). Кроме того, легко видеть, что чем больше длина вектора H_hkl обратной решетки, тем меньше межплоскостное расстояние в соответствующей серии плоскостей d_hkl основной решетки.

В общем виде справедливо следующее соотношение.

Вектор Н_hkl, проведенный из начала координат в любой узел обратной решетки ·hkl·*, ближайший к началу в данном узловом ряду, всегда перпендикулярен узловой сетке основной (кристаллографической) решетки, имеющей те же индексы, а длина этого вектора |H_hkl| обратно пропорциональна межплоскостному расстоянию d_hkl. Если обозначить единичный по длине вектор нормали к серии плоскостей (hkl) через N_hkl (где |N |=1), то сформулированное свойство можно записать в виде соотношения

Так как узловой ряд [hkl]* далее содержит узлы ·2h2k2l ·, ·3h3k3l ·, и т. д., то в более общей форме

где

В скалярной форме 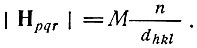. Соотношения (8) можно рассматривать как частные случаи этого общего соотношения.

Рис. 5. К доказательству соотношения(11)

Для доказательства справедливости формулы (11) умножим обе части этого равенства скалярно на один из осевых векторов решетки кристалла, например а. С учетом соотношений (5) и (6) в левой части имеем

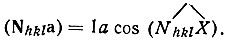
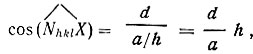
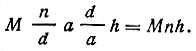
В правой части соотношения (11) N hkl по определению, есть единичный вектор нормали к серии плоскостей (hkl), следовательно, . На рис. 5 изображена ближайшая к началу координат сетка (hkl) и проведена нормаль к ней N_hkl. На оси X отмечен отрезок a/h, отсекаемый этой сеткой, а на нормали N_hkl— расстояние d_hkl. Очевидно, что , а вся правая часть (11). Повторив те же операции при скалярном

перемножении обеих частей равенства (11) на b и на с, убеждаемся, что все три компоненты (проекции на оси) векторов, представляющих левую и правую части равенства, совпадают. Значит, оба вектора H pqr и 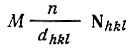равны по длине и совпадают по направлению.

Соотношения (10) и особенно (11) будут использованы в последующих разделах при выводе основных формул структурного анализа.

Соотношение (10) дает также основу для вывода формулы (3), связывающей межплоскостное расстояние некоторой серии плоскостей (hkl) с параметрами решетки a, b, c, α, β, γ. Положив М=1 и взяв скалярный квадрат от обеих частей равенства (10), получим

* ( См.: Бокий Г. Б., Порай-Кошиц М. А. Рентгеноструктурный анализ. Т. I. Изд-во МГУ, 1964. С. 316-317.)

Источник

ОБРАТНАЯ РЕШЕТКА

— периодпч. решёткав обратном пространстве, элементарные векторы трансляции к-рой b_i связаны с осн. векторами трансляции a_i исходной Браве решётки (прямой решётки) условиями

Узлы О. р. задаются соотношениями 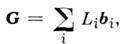где L_i— произвольные целые числа, i =1, 2, 3 для трёхмерной решётки,i= 1, 2 для двухмерной. Размерность О. р. совпадает с размерностьюпрямой решётки. Так, для трёхмерной прямой решётки О. р. является трёхмернойс элементарными векторами трансляции, равными в соответствии с (1):

Здесь V =( а ₁[ а₂ а₃])- объём элементарной ячейки прямой решётки; объём элементарной ячейки О.

Полезное

Смотреть что такое «ОБРАТНАЯ РЕШЕТКА» в других словарях:

ОБРАТНАЯ РЕШЕТКА — точечная трехмерная решетка в абстрактном обратном пространстве, где расстояния имеют размерность обратной длины. Понятие обратной решетки удобно для описания дифракции рентгеновских лучей, нейтронов и электронов на кристалле … Большой Энциклопедический словарь

обратная решетка — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN reciprocal lattice … Справочник технического переводчика

Обратная решетка — Обратная решётка точечная трехмерная решётка в абстрактном обратном пространстве, где расстояния имеют размерность обратной длины. Понятие обратной решётки удобно для описания дифракции рентгеновских лучей, нейтронов и электронов на кристалле.… … Википедия

обратная решетка — [reciprocal lattice] вспомогательная пространственная решетка, построенная на векторах a1, b1, c1 однозначно связанных с векторами трансляций а, b, с кристаллической решетки; скалярное произведение одноименных векторов равно 1, разноименное 0;… … Энциклопедический словарь по металлургии

обратная решётка — точечная трёхмерная решётка в абстрактном обратном пространстве, где расстояния имеют размерность обратной длины. Понятие «Обратной решётки» удобно для описания дифракции рентгеновских лучей, нейтронов и электронов на кристалле. * * * ОБРАТНАЯ… … Энциклопедический словарь

Решетка — [lattice] 1. Смотри Колосниковая решетка. 2. Смотри Пространственная и кристаллическая решетка: Смотри также: триклинная решетка тетрагональная решетка пространственная решетка … Энциклопедический словарь по металлургии

Решетка — решётка I ж. 1. Переплетающиеся ряды деревянных или металлических полос, прутьев или проволоки. отт. Частый забор, ограда из полос, планок, прутьев. 2. Устройство с отверстиями для задерживания чего либо, для прохождения воздуха и т.п. 3. То, что … Современный толковый словарь русского языка Ефремовой

Решетка — Решётка по В. И. Далю всякая несплошная вещь, со сквозниной, с промежками, пролётами; ряд установленных жердочек, шестиков, или переложенных, переплетённых вдоль и поперек, либо иным образом; В математике Решётка в теории множеств частично… … Википедия

триклинная решетка — [triclinic lattice] кристаллическая решетка, элементарная ячейка которой относится к триклинной сингонии. Смотри также: Решетка тетрагональная решетка пространственная решетка обратная решетка … Энциклопедический словарь по металлургии

Источник