зачем нужна квантовая механика
Квантовая механика – что это такое и зачем она нужна?
Квантовая механика родилась как необходимость, чтобы объяснить результаты некоторых опытов, которые не могла объяснить классическая теория.
Второй казус возник с планетарной моделью атома Резерфорда. Когда он представил свою модель, то мудрецы сразу же выдвинули теорию: электрон, вращается с большой скоростью вокруг ядра в результате чего должен излучать энергию и в конце концов упасть на ядро. А этот электрон никуда не падал и никуда не улетал. Но то ли эти мудрецы забыли или и не знали об опытах Кауфмана и наличие у ядра магнитного поля (может быть тогда об этом никто не знал) так как не учли все это в своих рассуждениях.
Пришлось Бору постулировать: у атома есть такие уровни (орбиты), где электрон летает и ничего не излучает. Все остолбенели и перестали искать силы, которые не позволяют электрону упасть на ядро, а про силы, удерживающие электрон в составе атома, даже и не думали, да и сейчас ученые и не подозревают, что такие силы существуют в виде обменного фотона.
Все бросились математикой доказывать существование таких утверждений. Я вот взял прямо с Википедии не большой список. Особо в этом преуспели:
К этому списку можно еще добавить многих.
Вы главное не пугайтесь этих формул. В этих формулах элементы, выделенные розовым цветом, называются гамильтонианом. Он описывает энергию, которая участвует в решении этой задачи. Это может быть потенциальная энергия, кинетическая энергия, упругая энергия и т.д. Вот в гамильтониане Шредингера расписаны кинетическая энергия, например, электрона и потенциальная энергия протона (электрическое поле). А под дифференциалами искомые функции, то есть при таком-то гамильтониане надо найти такую функцию, которая удовлетворяла бы этому уравнению. Обычно решение находится в виде синусов, косинусов и других колеблющихся функций. В общем волна и точка. Функция волновая.
Вот эту задачу для атома водорода и решает Ричард Фейнман в своих лекциях: “Том 9. Глава 17. Атом водорода и периодическая таблица”. http://t-z-n.ru/archives/tom9.pdf. Правда он допускает не поправимую ошибку – исключает, вернее не вводит в гамильтониан, магнитное поле протона, которое как раз и не позволяет электрону упасть на протон. Ну да ладно этого пока никто не понимает.
Дальше он градуирует потенциал на определенные участки с энергией En=ER/n*2. Называет число n – главным квантовым числом. Для кинетической энергии вводится число l, как полагает Фейнман оно квантует орбитальный момент.
Затем решает это уравнение и поучает такие результаты.
Как видите везде волны. Ясно что функция волновая. Но это волны чего? Как эта волна связана с частицей, чтобы объяснить корпускулярно-волновой дуализм? Волна относится к самому телу электрона, чего требует этот самый дуализм, или к поведению электрона, что никак не входит в дуализм? Надо бы объяснить дуализм самого электрона, без относительно того где он находится, а Фейнман решает задачу – где он находится, как частица. Женится, и обещать женится – разные вещи.
Не знаю, как эти теоретические расчеты Фейнмана вписываются в серии Ридберга, Лаймана, Бальмера и других.
Других описаний чего-либо я пока не нашел. Да думаю их по логике и быть то не должно. Действительно, если атом водорода Фейнман верно описал при помощи уравнения Шредингера, то с необходимостью такие же результаты должны будут получится у любого ученого, описывающего атом водорода пользующихся фомулами Неймана, Линдбада и другими.
По этой причине утверждение, что “квантовая механика адекватно описывает основные свойства и поведение атомов, ионов, молекул, конденсированных сред и других систем с электронно-ядерным строением” (Википедия) кажется весьма сомнительным.
К сожалению, не нахожу и не могу представить хоть какую-то значимую область явлений, где квантовая механика помогла бы что-нибудь решить.
Вы можете представить какое-то участие принципов этой механики в автомобиле строении. Автомобиль уже был, а волновой функции не было. Может быть паровозы или пароходы, у которых гребные винты рассчитываются с применением волновых функций. Все это было до гения Шредингера. У Эдисона вообще не было никакого образования, а его лампочки светят. Тогда следует искать следы применения этих функций в более поздних явлениях? Ракеты. Пользовались ли Мещерский или Циолковский квантовой механикой, да еще и с необходимостью, как с законами? Ой, ли. А компьютер? Вот булева алгебра в компьютерах применялась и применяется, а дуализм не применяется до сих пор, хотя и пытаются построить квантовый компьютер. Где, где может применятся идеология квантовой механики? В атомной сфере, в радио, в телекоммуникациях или в любых других процессах передачи информации или энергии?
Назовите мне хоть одну из областей бытия, в которой сидел бы ученый и рассчитывал бы поведение “атомов, ионов, молекул”. Может это в молекулярной биологии ученый рассчитывает, как происходит репликация, митоз, параметры вакцины и так далее? Покажите такого ученого, у которого на вооружении была бы волновая функция, за исключением преподавателей, для которых волновая функция – хлеб. Да легче найти самого замаскированного шпиона, чем такого ученого.
В заключение можно сказать, что такая квантовая механика с ее нынешними законами человечеству приносит больше вреда, нежели пользы.
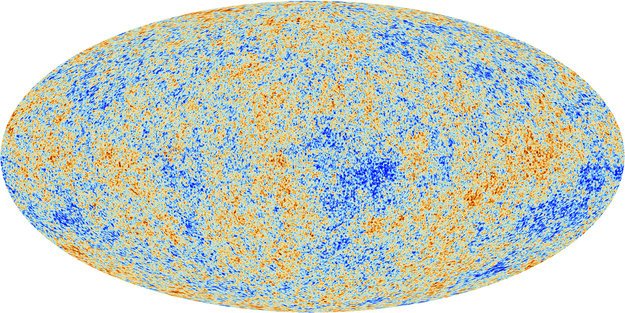
Сверхъестественное Вселенского масштаба: что такое тёмная материя, куда ведут черные дыры, и зачем нужна квантовая механика
Физика, как ни парадоксально звучит, — наука наиболее разношёрстная, неизученная и неполноценная. И это мнение не только научных журналистов, но и самих учёных, понимающих как много ещё им предстоит открыть. Взять ту же Теорию относительности Эйнштейна: она идеально работает для планет и галактик, но для микромира субатомных частиц она совершенно непригодна. В микроскопических масштабах правит квантовая физика.
Если даже теоретические модели физики не могут объединиться, то что уж говорить об экспериментальных наблюдениях. Здесь как в притче об истине и слоне: один слепой мудрец сказал, что истина — это огромное и необъятное, потрогав слона за брюхо, другой — что она длинная и гибкая, коснувшись хобота животного, а третий — что у истины кисточка на тонком стебельке — как у хвоста.
И всё же, существуют в мире науки неоспоримые результаты наблюдений и идеальные с математической точки зрения гипотезы, в которых действительно интересно разобраться. Ведь они могут открыть такие просторы для размышлений, что попытка осмыслить бесконечность Вселенной покажется детской загадкой о качелях.
Тёмная материя
Тёмную материю можно охарактеризовать всего двумя словами: «вездесущая» и «неуловимая». Если вспоминать школьный курс физики, то можно припомнить, что видов взаимодействия (по крайней мере, нам известных) существует всего четыре — гравитационное, электромагнитное, сильное и слабое. Всё, что мы можем увидеть или засечь каким-либо прибором, обязательно будет участвовать в электромагнитном взаимодействии, однако тёмная материя, как назло, этим не занимается.
Теоретики решили, что если есть материя, значит, она из чего-то состоит. В смысле, из каких-то частиц, похожих на наши атомы, или по крайней мере, протоны и электроны. Как только ни пытались назвать эти частицы физики — тёмными атомами, аксионами, космионами, тяжёлыми нейтрино. Наконец, сравнительно недавно с названием для частиц тёмной материи определились. Их назвали вимпами.
Астрономический спутник «Планк».
Вимп — грубая калька с английской аббревиатуры WIMP, которая расшифровывается как Weakly Interacting Massive Particles, то есть, «слабо взаимодействующие массивные частицы». Из четырёх видов взаимодействий вимпы участвуют только в двух — слабом, как видно из названия, и гравитационном, как видно из наблюдений. Астрономы постоянно сталкиваются с гравитационной тягой, которую оказывают скопления тёмной материи на наши родные звёзды и галактики.
На этом познания физиков о тёмной материи заканчиваются, если, конечно, не учитывать массу громоздких расчётов. Совершенно неясно, какой массой обладают эти частицы: одни расчёты указывают на 6-8 гигаэлектронвольт, другие — на 33 гигаэлектронвольта, а третьи дают вообще несопоставимые с реальностью данные.

Пока весь мир ждет, когда будут выделены средства на постройку более чувствительных и крупных детекторов, остается только фантазировать, что же такое тёмная материя и тёмная энергия, и что они скрывают под своей темнотой.
Чёрные дыры
Чёрные дыры — фактически мёртвые звёзды. Они не имеют ничего общего с тёмной материей и являются вполне обычными с определённой точки зрения объектами. После того, как массивное светило напрочь исчерпает свой запас топлива и взорвётся сверхновой, образуется собственно чёрная дыра.
Это тело представляет собой сверхплотную точку — так называемую сингулярность — аналогичную тому, что представляла собой Вселенная в момент Большого взрыва. Сингулярность окружена горизонтом событий — гипотетической границей, за которую не может выйти ни материя, ни свет, ни даже информация. К слову, знаменитый Стивен Хокинг немного несогласен с последним утверждением: его именем названо так называемое излучение Хокинга, представляющее собой частицы, которым всё же удалось выпрыгнуть за пределы горизонта событий.
После осознания того факта, что чёрные дыры удерживают своей гравитацией целые галактики и обладают массами, равными миллионам солнечных, но крайне малыми размерами, начинается самое интересное.
Квантовая механика
Квантовая механика скрывает за собой самые интересные тайны Вселенной. Выше уже было сказано: законы квантовой механики идеально функционируют для описания взаимодействий субатомных частиц, однако для описания природы массивных тел, будь то стул и стол или звезда и галактика, квантмех непригоден.
Но что будет, если включить фантазию? В этом разделе физики есть, как минимум, два явления, достойных внимания и ближайшего рассмотрения. Первое из них называется суперпозиция. Некая частица обладает сразу несколькими состояниями до тех пор, пока её не измерят — всё зависит от нас, наблюдателей. Здесь же уместно вспомнить замученного интернет-пользователями кота Шрёдингера : теоретик придумал этот мысленный эксперимент именно для иллюстрации понятия суперпозиции — кот жив и мёртв одновременно, пока коробку не откроют и наблюдатель не сыграет свою роль.
По принципу суперпозиции строятся квантовые компьютеры. В них вместо привычных битов функционируют кубиты (qubit, quantum bit — квантовый бит), которые принимают значения «0» и «1» одновременно. За счёт этого увеличивается скорость вычислений и, соответственно, производительность компьютера.
Другое квантовомеханическое явление называется квантовой запутанностью. Представьте себе две частицы, разведённые по разным концам Вселенной. Если они «запутаны» друг с другом, то как только одна из них примет определённое состояние, другая мгновенно пример противоположное. Если бы они сообщались посредством какого-либо электрического сигнала, то он шёл бы миллиарды лет, а тут смена происходит одновременно.

И если представить, что наша Вселенная — всего лишь голограмма, проекция от другой или других миров, это математически означает, что то, что мы видим как квантовую запутанность, есть червоточина, только в четырёхмерном мире.

На одной идее о квантовой запутанности можно зайти очень далеко. В конце концов, мгновенная передача какой-либо информации есть прямо нарушение принципа непреодолимости скорости света. Если когда-нибудь кто-нибудь придумает, как заставить запутанные частицы передавать нужную нам информацию — а пока что к этому не подобрались даже теоретики — то у нас появится шанс, к примеру, связаться с обитателями далёких планет. Если на них, конечно, вообще кто-то живет.
А если придумают как по запутанности передавать материю, то мечты фантастов о телепортации станут реальностью.
Кстати, за чудесами физики не надо лезть ни в чёрную дыру, ни нырять внутрь атома, достаточно выйти завтра утром на пробежку. Знайте, чем быстрее вы бежите сквозь пространство, тем медленнее движетесь сквозь время. Так что душ будете принимать не только постройневшим, но и помолодевшим.
Текст: Ася Горина, редактор «Вести Наука».
Квантовая механика
Слово «квант» происходит от латинского quantum («сколько, как много») и английского quantum («количество, порция, квант»). «Механикой» издавна принято называть науку о движении материи. Соответственно, термин «квантовая механика» означает науку о движении материи порциями (или, выражаясь современным научным языком науку о движении квантующейся материи). Термин «квант» ввел в обиход немецкий физик Макс Планк (см. Постоянная Планка) для описания взаимодействия света с атомами.
Квантовая механика часто противоречит нашим понятиям о здравом смысле. А всё потому, что здравый смысл подсказывает нам вещи, которые берутся из повседневного опыта, а в своем повседневном опыте нам приходится иметь дело только с крупными объектами и явлениями макромира, а на атомарном и субатомном уровне материальные частицы ведут себя совсем иначе. Принцип неопределенности Гейзенберга как раз и очерчивает смысл этих различий. В макромире мы можем достоверно и однозначно определить местонахождение (пространственные координаты) любого объекта (например, этой книги). Не важно, используем ли мы линейку, радар, сонар, фотометрию или любой другой метод измерения, результаты замеров будут объективными и не зависящими от положения книги (конечно, при условии вашей аккуратности в процессе замера). То есть некоторая неопределенность и неточность возможны — но лишь в силу ограниченных возможностей измерительных приборов и погрешностей наблюдения. Чтобы получить более точные и достоверные результаты, нам достаточно взять более точный измерительный прибор и постараться воспользоваться им без ошибок.
Теперь если вместо координат книги нам нужно измерить координаты микрочастицы, например электрона, то мы уже не можем пренебречь взаимодействиями между измерительным прибором и объектом измерения. Сила воздействия линейки или другого измерительного прибора на книгу пренебрежимо мала и не сказывается на результатах измерений, но чтобы измерить пространственные координаты электрона, нам нужно запустить в его направлении фотон, другой электрон или другую элементарную частицу сопоставимых с измеряемым электроном энергий и замерить ее отклонение. Но при этом сам электрон, являющийся объектом измерения, в результате взаимодействия с этой частицей изменит свое положение в пространстве. Таким образом, сам акт замера приводит к изменению положения измеряемого объекта, и неточность измерения обусловливается самим фактом проведения измерения, а не степенью точности используемого измерительного прибора. Вот с какой ситуацией мы вынуждены мириться в микромире. Измерение невозможно без взаимодействия, а взаимодействие — без воздействия на измеряемый объект и, как следствие, искажения результатов измерения.
О результатах этого взаимодействия можно утверждать лишь одно:
неопределенность пространственных координат × неопределенность скорости частицы > h/m,
или, говоря математическим языком:
где Δx и Δv — неопределенность пространственного положения и скорости частицы соответственно, h — постоянная Планка, а m — масса частицы.
Соответственно, неопределенность возникает при определении пространственных координат не только электрона, но и любой субатомной частицы, да и не только координат, но и других свойств частиц — таких как скорость. Аналогичным образом определяется и погрешность измерения любой такой пары взаимно увязанных характеристик частиц (пример другой пары — энергия, излучаемая электроном, и отрезок времени, за который она испускается). То есть если нам, например, удалось с высокой точностью измерили пространственное положение электрона, значит мы в этот же момент времени имеем лишь самое смутное представление о его скорости, и наоборот. Естественно, при реальных измерениях до этих двух крайностей не доходит, и ситуация всегда находится где-то посередине. То есть если нам удалось, например, измерить положение электрона с точностью до 10 –6 м, значит мы одновременно можем измерить его скорость, в лучшем случае, с точностью до 650 м/с.
Из-за принципа неопределенности описание объектов квантового микромира носит иной характер, нежели привычное описание объектов ньютоновского макромира. Вместо пространственных координат и скорости, которыми мы привыкли описывать механическое движение, например шара по бильярдному столу, в квантовой механике объекты описываются так называемой волновой функцией. Гребень «волны» соответствует максимальной вероятности нахождения частицы в пространстве в момент измерения. Движение такой волны описывается уравнением Шрёдингера, которое и говорит нам о том, как изменяется со временем состояние квантовой системы.
Картина квантовых событий в микромире, рисуемая уравнением Шрёдингера, такова, что частицы уподобляются отдельным приливным волнам, распространяющимся по поверхности океана-пространства. Со временем гребень волны (соответствующий пику вероятности нахождения частицы, например электрона, в пространстве) перемещается в пространстве в соответствии с волновой функцией, являющейся решением этого дифференциального уравнения. Соответственно, то, что нам традиционно представляется частицей, на квантовом уровне проявляет ряд характеристик, свойственных волнам.
Согласование волновых и корпускулярных свойств объектов микромира (см. Соотношение де Бройля) стало возможным после того, как физики условились считать объекты квантового мира не частицами и не волнами, а чем-то промежуточным и обладающим как волновыми, так и корпускулярными свойствами; в ньютоновской механике аналогов таким объектам нет. Хотя и при таком решении парадоксов в квантовой механике всё равно хватает (см. Теорема Белла), лучшей модели для описания процессов, происходящих в микромире, никто до сих пор не предложил.
Квантовая механика для всех, даром, и пусть никто не уйдёт обиженным: часть первая
Здравствуйте! Я хотел бы представить вашему вниманию отличное введение в квантовую механику, написанное Элиезером Юдковским; быть может, он известен вам по своему сайту lesswrong.com, посвящённому рационализму, предрассудкам, когнитивным парадоксам и ещё многим интересным вещам.
читать вторую часть →
Введение во введение
Предупреждаю сразу: этот цикл статей заметно отличается от традиционного введения в квантовую механику.
Во-первых, я не буду цитировать Ричарда Фейнмана, однажды заявившего, что «это нормально — не понимать квантовую механику, потому что никто её не понимает». Когда-то это было так, но времена меняются.
Я не скажу: «Квантовую механику невозможно понять, к ней просто нужно привыкнуть». (Эту цитату приписывают Джону фон Нейману; он жил в те дремучие времена, когда никто и в самом деле не понимал квантовую механику.)
Нельзя заканчивать объяснение словами «Если что-то непонятно, так и должно быть». Нет, так не должно быть. Может, проблема в вас. Может — в вашем учителе. В любом случае, её надо решать, а не сидеть сложа руки и успокаивать себя тем, что все остальные тоже ничего не понимают.
Я не буду говорить, что квантовая механика — это нечто странное, запутанное или недоступное для человеческого понимания. Да, она контринтуитивна — но это беда исключительно нашей интуиции. Квантовая механика возникла задолго до Солнца, планеты Земля или человеческой цивилизации. Она не собирается меняться ради вас. Вообще, не существует обескураживающих фактов, есть только теории, обескураженные фактами; а если теория не совпадает с практикой, это не делает ей чести.
Всегда стоит рассматривать реальность как совершенно обыденную вещь. С начала времён во Вселенной не случилось ничего необычного.
Наша цель — научиться чувствовать себя как дома в этом квантовом мире. Потому что мы и так дома.
На протяжении всего этого цикла я буду говорить о квантовой механике как о самой обычной теории; а там, где интуитивное представление о мире не совпадает с ней, я буду высмеивать интуицию за несоответствие реальности.
Во-вторых, я не собираюсь следовать традиционному порядку изучения квантовой механики, копирующему порядок, в котором её открывали.
Обычно всё начинается с рассказа о том, что материя иногда ведёт себя как кучка маленьких бильярдных шаров, сталкивающихся между собой, а иногда — как волны на поверхности бассейна. Это сопровождается несколькими примерами, иллюстирующими оба взгляда на материю.
Раньше, когда всё это только зарождалось и никто не имел ни малейшего понятия о математических основах физики, учёные всерьёз считали, что всё состоит из атомов, ведущих себя примерно как бильярдные шары. А потом они стали считать, что всё состоит из волн. А потом они опять вернулись к бильярдным шарам. Всё это привело к тому, что учёные окончательно запутались, и только через несколько десятилетий — к концу девятнадцатого века — им удалось расставить всё по своим местам.
Если применить этот исторический достоверный подход к обучению современных студентов (как сейчас и поступают), с ними закономерно случится то же, что случилось с ранними учёными, а именно — они впадут в полное и абсолютное замешательство. Рассказывать студентам, изучающим физику, о корпускулярно-волновом дуализме, это то же самое, что начинать курс химии лекцией о четырёх стихиях.
Электрон не похож ни на бильярдный шар, ни на гребень океанской волны. Электрон — это совершенно другой объект с математической точки зрения, и он остаётся таким при любых обстоятельствах. А если вы будете упорствовать в своём стремлении считать его и тем, и тем, как вам удобнее, предупреждаю: за двумя зайцами погонишься — ни одного не поймаешь.
Это не единственная причина, по которой исторический порядок — не лучший выбор. Давайте проследим за гипотетическим процессом с самого начала: люди замечают, что они окружены другими животными — внутри животных, оказывается, есть органы — а органы, если присмотреться внимательнее, состоят из тканей — под микроскопом видно, что ткани состоят из клеток — клетки состоят из протеинов и прочих химических соединений — химические соединения состоят из атомов — атомы состоят из протонов, нейтронов и электронов — а последние гораздо проще и понятнее животных, с которых всё началось, но были открыты на десятки тысяч лет позже.
Физику не начинают проходить с биологии. Тогда почему её нужно начинать с обсуждения лабораторных экспериментов и их результатов, которые даже в случае простейших опытов являются следствием множества сложных и запутанных процессов?
С одной стороны, я могу понять, почему во главу угла ставится эксперимент. Мы же о физике говорим, в конце концов.
С другой стороны, давать студентам в руки сложный математический аппарат только для того, чтобы они могли проанализировать простой опыт — это уже чересчур. Программистов, например, сначала учат складывать две переменные, а только потом — писать многопоточные приложения; и плевать на то, что вторые «ближе к реальной жизни».
Классическая механика не следует явным образом из квантовой механики. Более того, классическая механика находится на гораздо более высоком уровне. Сравните атомы и молекулы с кварками: миллионы известных науке химических веществ, сотня химических элементов, и всего шесть кварков. Сначала лучше понять простое, а только потом переходить к сложному.
Наконец, я буду рассматривать квантовую механику со строго реалистической позиции — наш мир является квантовым, наши уравнения описывают территорию, а не её карту, и привычный нам мир неявным образом существует в квантовом мире. Если среди моих читателей есть антиреалисты — пожалуйста, придержите свои комментарии. Квантовую механику гораздо труднее понять и представить, если сомневаешься в её справедливости. Я поговорю об этом подробнее в одной из следующих статей.
Я думаю, что той точки зрения, которую я буду излагать в этом введении, придерживается большинство физиков-теоретиков. Но вы всё же должны знать, что это не единственная возможная точка зрения, и немалая доля учёных сомневается в верности реалистической позиции. Хоть я и не собираюсь уделять внимание каким-либо другим теориям прямо сейчас, я чувствую себя обязанным упомянуть о том, что они есть.
Подводя итог, моя цель — научить вас думать как коренной житель квантового мира, а не как турист поневоле.
Покрепче вцепитесь в реальность. Мы начинаем.
Конфигурации и амплитуды
Посмотрите на рис. 1. В точке A находится полупосеребрённое зеркало, а в точках B и C — два детектора фотонов.
Этот простой эксперимент в своё время заставил учёных поломать головы. Дело в том, что в половине случаев фотон, выпущенный в сторону зеркала, регистрировался первым детектором, а в половине — на вторым. И учёные — внимание, приготовьтесь смеяться — предполагали, что зеркало то пропускало фотон, то отражало его.
Ха-ха-ха, представьте себе зеркало, которое может само выбирать, пропускать ему фотон или не пропускать! Если вы и можете это представить, то все равно не делайте этого — а не то вы запутаетесь так же, как и те учёные. Зеркало ведёт себя абсолютно одинаково в обоих случаях.
Если бы мы попробовали написать компьютерную программу, симулирующую этот эксперимент (а не просто предсказывающую результат), она бы выглядела примерно так…
В начале программы мы объявляем переменную, хранящую в себе определённый математический объект — конфигурацию. Она представляет некое описание состояния мира — в данном случае, «один фотон летит в точку А».
Введём ещё две конфигурации: «фотон летит из A в точку B» и «фотон летит из A в точку C». Мы пока не знаем амплитуды этих конфигураций; им будут присвоены значения в ходе выполнения программы.
В принципе, можно считать «первый детектор регистрирует фотон» и «второй детектор регистрирует фотон» отдельными конфигурациями, но это ничего не меняет; их амплитуды будут равны амплитудам двух предыдущих конфигураций соответственно. (На самом деле их ещё надо домножить на множитель, равный расстоянию от A до детекторов, но мы просто предположим, что все расстояния в нашем эксперименте являются множителями единицы.)
Итак, вот конечное состояние программы:
Разумеется, сколько бы раз мы ни запускали программу, конечное состояние останется таким же.
Теперь, по довольно сложным причинам, в которые я пока не буду вдаваться, не существует простого способа измерить амплитуду конфигурации. Состояние программы скрыто от нас.
Хоть мы и не можем измерить амплитуду непосредственно, кое-что у нас есть — а именно, волшебная измерительная штуковина, которая может сообщить нам квадрат модуля амплитуды конфигурации. Другими словами, для амплитуды (a + bi) штуковина ответит числом (a² + b²).
Точнее было бы сказать, что волшебная штуковина находит всего лишь отношение квадратов модулей друг к другу. Но даже этой информации оказывается достаточно, чтобы понять, что происходит внутри программы и по каким законам она работает.
С помощью штуковины мы можем легко узнать, что квадраты модулей конфигураций «сработал первый детектор» и «сработал второй детектор» равны. А проведя некоторые более сложные эксперименты, мы сможем также узнать отношение самих амплитуд — i к 1.
Кстати, а что это за волшебная измерительная штуковина такая?
Ну, когда такие эксперименты проводят в реальной жизни, в качестве волшебной штуковины служит то, что эксперимент проводят пару тысяч раз и просто считают, сколько раз фотон оказался в первом детекторе, а сколько — во втором. Отношение этих значений и будет отношением квадратов модулей амплитуд. Почему это будет так — вопрос другой, гораздо более сложный. А пока можно пользоваться штуковиной и без понимания того, как да почему она работает. Всему своё время.
Вы можете спросить: «А зачем вообще нужна квантовая теория, если её предсказания совпадают с предсказаниями „бильярдной” теории?» Есть две причины. Во-первых, реальность, что бы вы там ни думали, всё-таки подчиняется квантовым законам — амплитуды, комплексные числа и всё такое. А во-вторых, «бильярдная» теория не работает для любого мало-мальски сложного эксперимента. Хотите пример? Пожалуйста.
На рис. 2 вы можете видеть два зеркала в точках B и C, и два полу-зеркала в точках A и D. Позже я объясню, почему отрезок DE проведён пунктиром; на расчётах это никак не скажется.
Давайте применим правила, которые мы уже знаем.
В начале у нас есть конфигурация «фотон летит в A», её амплитуда — (-1 + 0i).
Считаем амплитуды конфигураций «фотон летит из A в B» и «фотон летит из A в C»:
Интуитивно ясно, что обычное зеркало ведёт себя как половина полу-зеркала: всегда отражает фотон, всегда умножает амплитуду на i. Итак:
Важно понять, что «из B в D» и «из C в D» — это две разные конфигурации. Нельзя просто написать «фотон летит в D», потому что от угла, под которым этот фотон приходит в D, зависит то, что с ним случится дальше.
Отношение квадратов модулей амплитуд — 0 к 4; из расчётов следует, что первый детектор вообще не будет срабатывать! Поэтому-то отрезок DE и был проведён пунктиром на рис. 2.
Если бы полу-зеркала отражали или пропускали фотон случайным образом, оба детектора реагировали бы примерно с одинаковой частотой. Но это не совпадает с результатами экспериментов. Вот и всё.
Вы могли бы возразить: «А вот и не всё! Предположим, например, что когда зеркало отражает фотон, с ним происходит что-то такое, что второй раз он уже не отразится? И, наоборот, когда зеркало пропускает фотон, в следующий раз ему придётся отразиться.»
Во-первых, бритва Оккама. Не стоит выдумывать сложное объяснение, если уже существует простое (если, конечно, считать квантовую механику простой…) А во-вторых, я могу придумать другой опыт, который опровергнет и эту альтернативную теорию.
Поместим маленький непрозрачный объект между B и D, чтобы амплитуда конфигурации «фотон летит из B в D» всегда равнялась нулю.
Это невозможно объяснить, если считать, что фотон — это маленький бильярдный шарик, который отражается от зеркал.
Дело в том, что об амплитуде нельзя думать, как о вероятности. В теории вероятностей, если событие X может произойти или не произойти, то вероятность события Z равна P(Z|X)P(X) + P(Z|¬X)P(¬X), где все вероятности положительны. Если вы знаете, что вероятность Z при условии, что X случилось, равна 0.5, а вероятность X — 0.3, то полная вероятность Z по меньшей мере 0.15, независимо от того, что произойдёт, если X не случится. Не бывает отрицательных вероятностей. Возможные и невозможные события не могут аннулировать друг друга. А амплитуды — могут.
Вот пример неправильного мышления: «Фотон летит в B или в C, но он мог полететь по-другому, и это влияет на вероятность того, что он полетит в E…»
События, которые не случились, не имеют никакого влияния на мир. Единственное, что может повлиять на мир — это наше воображение. «О боже, эта машина чуть не сбила меня», думаете вы, и решаете уйти в монастырь, чтобы больше никогда не встречаться с опасными машинами. Но реально по-прежнему не само событие, а лишь ваше воображение, содержащееся в вашем мозгу — который можно из вас достать, пощупать и положить назад, чтобы убедиться, что он вполне реален.
Реально всё, что влияет на мир. (Если вы полагаете, что это не так, попробуйте дать определение слову «реальный».) Конфигурации и амплитуды непосредственно влияют на мир, так что они тоже реальны. Сказать, что конфигурация — это «то, что могло случиться», так же странно, как сказать, что стул — это «то, что могло случиться».
А что это тогда — конфигурация?
На самом деле всё немного сложнее, чем вам могло показаться после прочтения этой статьи.
Каждая конфигурация описывает все частицы во Вселенной. Амплитуда — это непрерывное распределение по всему пространству конфигураций, а не дискретное, как мы рассматривали сегодня. И в самом деле, фотоны же не телепортируются из одного места в другое мгновенно, а каждое различное состояние мира описывается новой конфигурацией. В конце концов мы и до этого доберёмся.
Если вы ничего не поняли из этого абзаца, не беспокойтесь, я всё объясню. Потом.