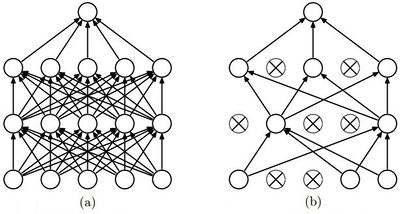
зачем нужна функция активации в нейросети
Практики реализации нейронных сетей
Содержание
Аугментация данных [ править ]
При глубоком обучении иногда можно столкнуться с ситуацией, когда набор данных имеет ограниченный размер. Но чтобы получить лучшие результаты обобщение модели, необходимо иметь больше данных, в том числе и различные их вариации. То есть необходимо увеличить размер исходного набора искусственным образом, и это можно сделать с помощью аугментации данных.
| Определение: |
| Аугментация данных (англ. data augmentation) — это методика создания дополнительных данных из имеющихся данных. |
Чаще всего, проблема ограниченного набора данных возникает при решении задач, связанных с обработкой изображений. Следующие способы аугментации изображений являются самыми популярными:
Также, можно применять различные комбинации, к примеру, вырезать часть изображения, повернуть его и изменить цвет фона.
Продвинутыми способами аугментации данных является семейство порождающих состязательных сетей.
Дропаут [ править ]
Одной из проблем глубокого обучения нейронных сетей является переобучение. И метод дропаут — популярный способ решения этой проблемы, благодаря простому алгоритму и хорошим практическим результатам.
| Определение: |
| Дропаут (англ. dropout) — метод регуляризации нейронной сети для предотвращения переобучения. |
В обычной нейронной сети явление переобучения появляется из-за так называемой совместной адаптации (англ. co-adaptation), то есть при обновлении весов нейрона, во время обучения методом обратного распространения ошибки, учитывается деятельность остальных нейронов с целью минимизировать функцию потерь. Поэтому веса нейронов могут меняться, исправляя при этом ошибки других нейронов. Метод дропаута как раз предотвращает эту адаптацию.
Алгоритм дропаут [ править ]
Обратный дропаут [ править ]
Обратная модификация дропаута на практике используется чаще обычной, потому что в ней не нужно менять каждый раз модель для проведения этапа тестирования.
Функции активации [ править ]
Одним из важнейших аспектов глубокой нейронной сети являются функции активации.
| Определение: |
| Функция активации (англ. activation function) [math]a(x)[/math] определяет выходное значение нейрона в зависимости от результата взвешенной суммы входов и порогового значения. |
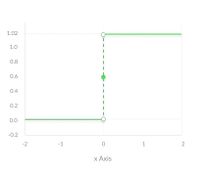
Ступенчатая функция [ править ]
Ступенчатая функция (англ. binary step function) является пороговой функцией активации. То есть если [math]z[/math] больше или меньше некоторого значения, то нейрон становится активированным. Такая функция отлично работает для бинарной классификации. Но она не работает, когда для классификации требуется большее число нейронов и количество возможных классов больше двух.
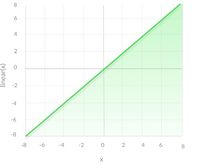
Линейная функция [ править ]
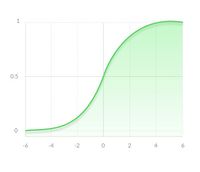
Сигмоидная функция [ править ]
Несмотря на множество сильных сторон сигмоидной функции, у нее есть значительный недостаток. Производная такой функции крайне мала во всех точках, кроме сравнительно небольшого промежутка. Это сильно усложняет процесс улучшения весов с помощью градиентного спуска. Более того, эта проблема усугубляется в случае, если модель содержит много слоев. Данная проблема называется проблемой исчезающего градиента. [1]
Что касается использования сигмоидной функции, то ее преимущество над другими — в нормализации выходного значения. Иногда, это бывает крайне необходимо. К примеру, когда итоговое значение слоя должно представлять вероятность случайной величины. Кроме того, эту функцию удобно применять при решении задачи классификации, благодаря свойству «прижимания» к асимптотам.
Функция гиперболического тангенса [ править ]
Обычно, [math]tanh[/math] является предпочтительнее сигмоиды в случаях, когда нет необходимости в нормализации. Это происходит из-за того, что область определения данной функции активации центрирована относительно нуля, что снимает ограничение при подсчете градиента для перемещения в определенном направлении. Кроме того, производная гиперболического тангенса значительно выше вблизи нуля, давая большую амплитуду градиентному спуску, а следовательно и более быструю сходимость.
Функция ReLU [ править ]
Функцию активации ReLU следует использовать, если нет особых требований для выходного значения нейрона, вроде неограниченной области определения. Но если после обучения модели результаты получились не оптимальные, то стоит перейти к другим функциям, которые могут дать лучший результат.
Функция Leaky ReLU [ править ]
На практике LReLU используется не так часто. Практический результат использования LReLU вместо ReLU отличается не слишком сильно. Однако в случае использования Leaky требуется дополнительно настраивать гиперпараметр (уровень наклона при отрицательных значениях), что требует определенных усилий. Еще одной проблемой является то, что результат LReLU не всегда лучше чем при использовании обычного ReLU, поэтому чаще всего такой подход используют как альтернатива. Довольно часто на практике используется PReLU (Parametric ReLU), который позволяет добиться более значительных улучшений по сравнению с ReLU и LReLU. Также, в случае параметрической модификации ReLU, угол наклона не является гиперпараметром и настраивается нейросетью.
Сверточная нейронная сеть, часть 1: структура, топология, функции активации и обучающее множество
Предисловие
Данные статьи (часть 2) являются частью моей научной работы в ВУЗе, которая звучала так: «Программный комплекс детектирования лиц в видеопотоке с использованием сверточной нейронной сети». Цель работы была — улучшение скоростных характеристик в процессе детектирования лиц в видеопотоке. В качестве видеопотока использовалась камера смартфона, писалось десктопное ПС (язык Kotlin) для создания и обучения сверточной нейросети, а также мобильное приложение под Android (язык Kotlin), которая использовала обученную сеть и «пыталась» распознать лица из видеопотока камеры. Результаты скажу получились так себе, использовать точную копию предложенной мной топологии на свой страх и риск (я бы не рекомендовал).
Введение
Наилучшие результаты в области распознавания лиц показала Convolutional Neural Network или сверточная нейронная сеть (далее – СНС), которая является логическим развитием идей таких архитектур НС как когнитрона и неокогнитрона. Успех обусловлен возможностью учета двумерной топологии изображения, в отличие от многослойного персептрона.
Сверточные нейронные сети обеспечивают частичную устойчивость к изменениям масштаба, смещениям, поворотам, смене ракурса и прочим искажениям. Сверточные нейронные сети объединяют три архитектурных идеи, для обеспечения инвариантности к изменению масштаба, повороту сдвигу и пространственным искажениям:
Именно поэтому в своей работе я использовал сверточную нейронную сеть, основанную на принципах неокогнитрона и дополненную обучением по алгоритму обратного распространения ошибки.
Структура сверточной нейронной сети
СНС состоит из разных видов слоев: сверточные (convolutional) слои, субдискретизирующие (subsampling, подвыборка) слои и слои «обычной» нейронной сети – персептрона, в соответствии с рисунком 1.

Рисунок 1 – топология сверточной нейронной сети
Первые два типа слоев (convolutional, subsampling), чередуясь между собой, формируют входной вектор признаков для многослойного персептрона.
Свое название сверточная сеть получила по названию операции – свертка, суть которой будет описана дальше.
Сверточные сети являются удачной серединой между биологически правдоподобными сетями и обычным многослойным персептроном. На сегодняшний день лучшие результаты в распознавании изображений получают с их помощью. В среднем точность распознавания таких сетей превосходит обычные ИНС на 10-15%. СНС – это ключевая технология Deep Learning.
Основной причиной успеха СНС стало концепция общих весов. Несмотря на большой размер, эти сети имеют небольшое количество настраиваемых параметров по сравнению с их предком – неокогнитроном. Имеются варианты СНС (Tiled Convolutional Neural Network), похожие на неокогнитрон, в таких сетях происходит, частичный отказ от связанных весов, но алгоритм обучения остается тем же и основывается на обратном распространении ошибки. СНС могут быстро работать на последовательной машине и быстро обучаться за счет чистого распараллеливания процесса свертки по каждой карте, а также обратной свертки при распространении ошибки по сети.
На рисунке ниже продемонстрирована визуализация свертки и подвыборки:
Топология сверточной нейросети
Определение топологии сети ориентируется на решаемую задачу, данные из научных статей и собственный экспериментальный опыт.
Можно выделить следующие этапы влияющие на выбор топологии:

Рисунок 2 — Топология сверточной нейросети
Входной слой
Входные данные представляют из себя цветные изображения типа JPEG, размера 48х48 пикселей. Если размер будет слишком велик, то вычислительная сложность повысится, соответственно ограничения на скорость ответа будут нарушены, определение размера в данной задаче решается методом подбора. Если выбрать размер слишком маленький, то сеть не сможет выявить ключевые признаки лиц. Каждое изображение разбивается на 3 канала: красный, синий, зеленый. Таким образом получается 3 изображения размера 48х48 пикселей.
Входной слой учитывает двумерную топологию изображений и состоит из нескольких карт (матриц), карта может быть одна, в том случае, если изображение представлено в оттенках серого, иначе их 3, где каждая карта соответствует изображению с конкретным каналом (красным, синим и зеленым).
Входные данные каждого конкретного значения пикселя нормализуются в диапазон от 0 до 1, по формуле:
Сверточный слой
Сверточный слой представляет из себя набор карт (другое название – карты признаков, в обиходе это обычные матрицы), у каждой карты есть синаптическое ядро (в разных источниках его называют по-разному: сканирующее ядро или фильтр).
Количество карт определяется требованиями к задаче, если взять большое количество карт, то повысится качество распознавания, но увеличится вычислительная сложность. Исходя из анализа научных статей, в большинстве случаев предлагается брать соотношение один к двум, то есть каждая карта предыдущего слоя (например, у первого сверточного слоя, предыдущим является входной) связана с двумя картами сверточного слоя, в соответствии с рисунком 3. Количество карт – 6.

Рисунок 3 — Организация связей между картами сверточного слоя и предыдущего
Размер у всех карт сверточного слоя – одинаковы и вычисляются по формуле 2:
Ядро представляет из себя фильтр или окно, которое скользит по всей области предыдущей карты и находит определенные признаки объектов. Например, если сеть обучали на множестве лиц, то одно из ядер могло бы в процессе обучения выдавать наибольший сигнал в области глаза, рта, брови или носа, другое ядро могло бы выявлять другие признаки. Размер ядра обычно берут в пределах от 3х3 до 7х7. Если размер ядра маленький, то оно не сможет выделить какие-либо признаки, если слишком большое, то увеличивается количество связей между нейронами. Также размер ядра выбирается таким, чтобы размер карт сверточного слоя был четным, это позволяет не терять информацию при уменьшении размерности в подвыборочном слое, описанном ниже.
Ядро представляет собой систему разделяемых весов или синапсов, это одна из главных особенностей сверточной нейросети. В обычной многослойной сети очень много связей между нейронами, то есть синапсов, что весьма замедляет процесс детектирования. В сверточной сети – наоборот, общие веса позволяет сократить число связей и позволить находить один и тот же признак по всей области изображения.
Неформально эту операцию можно описать следующим образом — окном размера ядра g проходим с заданным шагом (обычно 1) все изображение f, на каждом шаге поэлементно умножаем содержимое окна на ядро g, результат суммируется и записывается в матрицу результата, как на рисунке 4.

Рисунок 4 — Операция свертки и получение значений сверточной карты (valid)

Операция свертки и получение значений сверточной карты. Ядро смещено, новая карта получается того же размера, что и предыдущая (same)
При этом в зависимости от метода обработки краев исходной матрицы результат может быть меньше исходного изображения (valid), такого же размера (same) или большего размера (full), в соответствии с рисунком 5.

Рисунок 5 — Три вида свертки исходной матрицы
В упрощенном виде этот слой можно описать формулой:
При этом за счет краевых эффектов размер исходных матриц уменьшается, формула:
Подвыборочный слой
Подвыборочный слой также, как и сверточный имеет карты, но их количество совпадает с предыдущим (сверточным) слоем, их 6. Цель слоя – уменьшение размерности карт предыдущего слоя. Если на предыдущей операции свертки уже были выявлены некоторые признаки, то для дальнейшей обработки настолько подробное изображение уже не нужно, и оно уплотняется до менее подробного. К тому же фильтрация уже ненужных деталей помогает не переобучаться.
В процессе сканирования ядром подвыборочного слоя (фильтром) карты предыдущего слоя, сканирующее ядро не пересекается в отличие от сверточного слоя. Обычно, каждая карта имеет ядро размером 2×2, что позволяет уменьшить предыдущие карты сверточного слоя в 2 раза. Вся карта признаков разделяется на ячейки 2х2 элемента, из которых выбираются максимальные по значению.
Обычно в подвыборочном слое применяется функция активации RelU. Операция подвыборки (или MaxPooling – выбор максимального) в соответствии с рисунком 6.

Рисунок 6 — Формирование новой карты подвыборочного слоя на основе предыдущей карты сверточного слоя. Операция подвыборки (Max Pooling)
Формально слой может быть описан формулой:
Полносвязный слой
Последний из типов слоев это слой обычного многослойного персептрона. Цель слоя – классификация, моделирует сложную нелинейную функцию, оптимизируя которую, улучшается качество распознавания.
Нейроны каждой карты предыдущего подвыборочного слоя связаны с одним нейроном скрытого слоя. Таким образом число нейронов скрытого слоя равно числу карт подвыборочного слоя, но связи могут быть не обязательно такими, например, только часть нейронов какой-либо из карт подвыборочного слоя быть связана с первым нейроном скрытого слоя, а оставшаяся часть со вторым, либо все нейроны первой карты связаны с нейронами 1 и 2 скрытого слоя. Вычисление значений нейрона можно описать формулой:
Выходной слой
Выбор функции активации
В данной работе в качестве функции активации в скрытых и выходном слоях применяется гиперболический тангенс, в сверточных слоях применяется ReLU. Рассмотрим наиболее распространенные функций активации, применяемые в нейронных сетях.
Функция активации сигмоиды
Эта функция относится к классу непрерывных функций и принимает на входе произвольное вещественное число, а на выходе дает вещественное число в интервале от 0 до 1. В частности, большие (по модулю) отрицательные числа превращаются в ноль, а большие положительные – в единицу. Исторически сигмоида находила широкое применение, поскольку ее выход хорошо интерпретируется, как уровень активации нейрона: от отсутствия активации (0) до полностью насыщенной активации (1). Сигмоида (sigmoid) выражается формулой:
График сигмоидальной функции в соответствии с рисунком ниже:
Крайне нежелательное свойство сигмоиды заключается в том, что при насыщении функции с той или иной стороны (0 или 1), градиент на этих участках становится близок к нулю.
Напомним, что в процессе обратного распространения ошибки данный (локальный) градиент умножается на общий градиент. Следовательно, если локальный градиент очень мал, он фактически обнуляет общий градиент. В результате, сигнал почти не будет проходить через нейрон к его весам и рекурсивно к его данным. Кроме того, следует быть очень осторожным при инициализации весов сигмоидных нейронов, чтобы предотвратить насыщение. Например, если исходные веса имеют слишком большие значения, большинство нейронов перейдет в состояние насыщения, в результате чего сеть будет плохо обучаться.
Сигмоидальная функция является:
Функция активации гиперболический тангенс
В данной работе в качестве активационной функции для скрытых и выходного слоев используется гиперболический тангенс. Это обусловлено следующими причинами:
Функция активации ReLU
Известно, что нейронные сети способны приблизить сколь угодно сложную функцию, если в них достаточно слоев и функция активации является нелинейной. Функции активации вроде сигмоидной или тангенциальной являются нелинейными, но приводят к проблемам с затуханием или увеличением градиентов. Однако можно использовать и гораздо более простой вариант — выпрямленную линейную функцию активации (rectified linear unit, ReLU), которая выражается формулой:
График функции ReLU в соответствии с рисунком ниже:
Преимущества использования ReLU:
Обучающие выборки использующиеся в экспериментах
Обучающая выборка состоит из положительных и отрицательных примеров. В данном случае из лиц и “не лиц”. Соотношение положительных к отрицательным примерам 4 к 1, 8000 положительных и 2000 отрицательных.
В качестве положительной обучающей выборки использовалась база данных LFW3D [7]. Она содержит цветные изображения фронтальных лиц типа JPEG, размером 90×90 пикселей, в количестве 13000. База данных предоставляется по FTP, доступ осуществляется по паролю. Для получения пароля необходимо заполнить на главной странице сайта простую форму, где указать свое имя и электронную почту. Пример лиц из базы данных показан в соответствии с рисунком ниже:
В качестве отрицательных обучающих примеров использовалась база данных SUN397 [8], она содержит огромное количество всевозможных сцен, которые разбиты по категориям. Всего 130000 изображений, 908 сцен, 313000 объектов сцены. Общий вес этой базы составляет 37 GB. Категории изображений весьма различны и позволяют выбирать более конкретную среду, где будет использоваться конечное ПС. Например, если априори известно, что детектор лиц предназначен только для распознавания внутри помещения, то нет смысла использовать обучающую выборку природы, неба, гор и т.д. По этой причине автором работы были выбраны следующие категории изображений: жилая комната, кабинет, классная комната, компьютерная комната. Примеры изображений из обучающей выборки SUN397 показаны в соответствии с рисунком ниже:
Результаты
Прямое распространение сигнала от входного изображения размером 90х90 пикселей занимает 20 мс (на ПК), 3000 мс в мобильном приложении. При детектировании лица в видеопотоке в разрешении 640х480 пикселей, возможно детектировать 50 не перекрытых областей размером 90х90 пикселей. Полученные результаты с выбранной топологией сети хуже по сравнению с алгоритмом Виолы-Джонса.
Выводы
Сверточные нейронные сети обеспечивают частичную устойчивость к изменениям масштаба, смещениям, поворотам, смене ракурса и прочим искажениям.
Ядро — представляет из себя фильтр, который скользит по всему изображению и находит признаки лица в любом его месте (инвариантность к смещениям).
Подвыборочный слой дает:
Обучение сверточной нейронной сети описано во второй части.
Ссылки
— Виды нейронных сетей (подобная схема классификации нейронных сетей)
— Нейронные сети для начинающих: раз и два.
Функции активации в нейронных сетях
Дата публикации Sep 6, 2017
Что такое функция активации?
Это просто функция, которую вы используете, чтобы получить выходные данные узла. Это также известно какФункция передачи,
Почему мы используем функции активации с нейронными сетями?
Функции активации можно в основном разделить на 2 типа:
К вашему сведению: шпаргалка приведена ниже.
Линейная или идентификационная функция активации
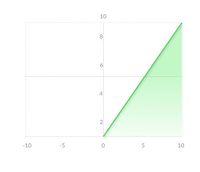
Как видите, функция является линейной или линейной. Поэтому выходные данные функций не будут ограничиваться каким-либо диапазоном.
Уравнение:f (x) = x
Диапазон :(бесконечность до бесконечности)
Это не помогает со сложностью или различными параметрами обычных данных, которые передаются в нейронные сети.
Нелинейная функция активации
Нелинейные функции активации являются наиболее часто используемыми функциями активации. Нелинейность помогает заставить график выглядеть примерно так
Это облегчает модели обобщение или адаптацию к различным данным и позволяет различать выходные данные.
Основные термины, необходимые для понимания нелинейных функций:
Производная или Дифференциальная:Изменение по оси у с.р. изменение в оси x.Он также известен как наклон.
Монотонная функция:Функция, которая либо полностью не увеличивается, либо не уменьшается.
Нелинейные функции активации в основном делятся на основе ихдиапазон или кривые—
1. Сигмовидная или логистическая функция активации
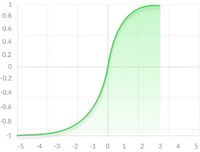
Кривая сигмовидной функции выглядит как S-образная форма.
Основная причина, по которой мы используем сигмовидную функцию, заключается в том, что она существует между(От 0 до 1).Поэтому он особенно используется для моделей, где мы должныпредсказать вероятностьв качестве выхода. Так как вероятность чего-либо существует только между0 и 1,сигмоид является правильным выбором.
ФункциядифференцируемаЭто означает, что мы можем найти наклон сигмовидной кривой в любых двух точках.
Функциямонотонныйно производной функции нет.
Логистическая сигмоидная функция может вызвать застревание нейронной сети во время обучения.
функция softmaxэто более обобщенная функция логистической активации, которая используется для мультиклассовой классификации.
2. Функция активации Танга или гиперболического тангенса
tanh также похожа на логистическую сигмоиду, но лучше. Диапазон функции tanh составляет от (-1 до 1). tanh также сигмоидальный (s-образный).
Преимущество состоит в том, что отрицательные входные данные будут отображаться строго отрицательными, а нулевые входные данные будут отображаться вблизи нуля на графике tanh.
Функциядифференцируема,
Функциямонотонныйв то время как егопроизводная не монотонная,
Функция tanh в основном используется для классификации между двумя классами.
Функции tanh и logistic sigmoid используются в сетях прямой связи.
3. Функция активации ReLU (выпрямленный линейный блок)
В настоящее время ReLU является наиболее используемой функцией активации в мире. Так как она используется практически во всех сверточных нейронных сетях или для глубокого обучения.
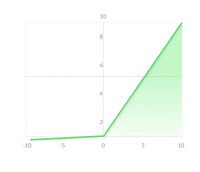
Как видите, ReLU наполовину выпрямлен (снизу). f (z) равно нулю, когда z меньше нуля, а f (z) равно z, когда z выше или равно нулю.
Диапазон:[От 0 до бесконечности)
Функция и ее производнаяобамонотонный,
Но проблема в том, что все отрицательные значения сразу становятся равными нулю, что снижает способность модели соответствовать или обучаться на основе данных должным образом. Это означает, что любой отрицательный входной сигнал, данный функции активации ReLU, немедленно превращает значение в ноль на графике, что, в свою очередь, влияет на результирующий график, не соответствующим образом отображая отрицательные значения.
4. Leaky ReLU
Это попытка решить проблему умирающего ReLU
Утечка помогает увеличить диапазон функции ReLU. Обычно значение 0,01 или около того.
когдаа не 0,01тогда это называетсяРандомизированный ReLU,
СледовательнодиапазонУтечек ReLU (бесконечность до бесконечности).
Обе утечки и рандомизированные функции ReLU являются монотонными по своей природе. Также их производные также монотонны по своей природе.
Почему производная / дифференциация используется?
При обновлении кривой, чтобы знать вв каком направленииа такжекак многоизменить или обновить кривую в зависимости от наклона. Вот почему мы используем дифференцирование почти в каждой части машинного обучения и глубокого обучения
Я буду публиковать 2 сообщения в неделю, поэтому не пропустите урок.
Итак, следуйте за мнойсредний,facebook,щебет,LinkedIn,Google+,Quoraчтобы увидеть похожие посты.
Любые комментарии или если у вас есть какие-либо вопросы,напишите это в комментарии.
Хлопай! Поделиться этим! Подписывайтесь на меня!