зачем нужен дифференциал в математике
Что такое дифференциал функции?
Понятие дифференциала функции связано с такими важными математическими разделами как дифференциальное и интегральное исчисление и тесно связано с понятием производной функции. Наиболее часто дифференциал применяется для приближенных вычислений, а также для оценки погрешностей формул и измерений.
Дифференциал функции — это линейная часть приращения функции. Говоря о значении дифференциала функции, рассматривают конкретную точку функции и бесконечно малое изменение аргумента.
История открытия дифференциала
Чаще всего открытие дифференциально-интегрального исчисления принято связывать с именем Исаака Ньютона, однако, этот факт активно оспаривают учёные со всего света.
Действительно, открытие целого нового направления в науке, столь значимого для её развития, было бы ошибочно считать заслугой только одного учёного. Изначально интегрирование связывали с вычислением площадей и объёмов криволинейных фигур. Такие задачи, как известно, решались ещё во времена Архимеда, поэтому его имя также имеет отношение к открытию дифференциального исчисления.
Также дифференцирование имеет отношение к решению задач на проведение касательных к различным кривым. Данное направление активно развивали греческие математики. В те времена математики столкнулись с трудностью, которую не смогли решить в дальнейшем и представители Нового времени.
Дело в том, что для определения направления прямой требовалось знать координаты как минимум двух точек, а касательная имеет лишь одну точку соприкосновения с кривой. Этот факт натолкнул учёных на мысль о том, что в одной точке кривая может иметь несколько касательных. В то время ученые пришли к выводу, что прямая состоит не из точек, а из отрезков минимальной длины. Таким образом, они считали направление касательной в некоторой точке совпадающим с направлением атомарного отрезка в данной точке.
В дальнейшем учёные Нового времени опровергли данную теорию. В этот период огромный вклад в развитие науки внёс Исаак Ньютон. Ученый сформулировал определения и принципы решения производных, а также основы дифференциального исчисления, которых придерживаются учёные и в наши дни.
Дифференциальное исчисление широко применяется в математике и других науках для решения различных задач.
Геометрический смысл дифференциала
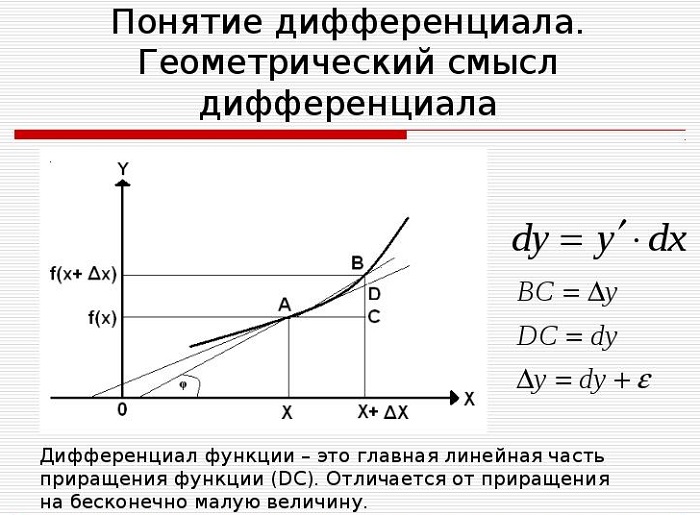
Геометрический смысл дифференциала заключается в следующем: дифференциал функции f(x) равен приращению ординаты касательной к графику функции, которая проведена через некоторую точку с координатами (x,y) при изменении координаты x на величину Δх=dx.
Дифференциал является главной линейной частью функции относительно приращения аргумента. Чем меньше приращение функции, тем большая доля приращения приходится на эту линейную часть.
Таким образом, при бесконечно малом Δх, приращение функции можно считать равным ее дифференциалу. Это свойство дифференциала позволяет использовать его для приблизительных вычислений и оценки погрешностей измерений.
Применение дифференциала в приближенных вычислениях
Поскольку дифференциал функции является частью ее приращения, то при бесконечно малом приращении аргумента он приблизительно равен приращению функции. При этом чем меньше приращение аргумента, тем точнее значение функции. Этот факт даёт возможность использования дифференциалов для приближённых вычислений.
С помощью таких вычислений можно решать различные виды задач. Приближённые вычисления практически всегда связаны с наличием погрешности.
Использование дифференциала для оценки погрешностей
Результаты измерений в большинстве случаев содержат ошибку, обусловленную неточностью измерительных приборов.
Число, несколько превышающее или равное этой неточности, называется «предельной абсолютной погрешностью».
Отношение предельной погрешности к значению измеряемой величины называют «предельной относительной погрешностью».
Для оценки величины погрешностей измерений используют дифференциальное исчисление.
При выполнении некоторых расчётов в исследованиях, проектировании, анализе полученных опытных путём данных часто возникает необходимость предварительной прикидки результата, которую удобно выполнять, используя дифференциал функции. Приближённые вычисления, выполненные с его помощью, могут дать новые направления дальнейшего изучения объектов и их разработок.
Понятие и геометрический смысл дифференциала
Пусть y = f (x) имеет производную
Применяя свойства предела функции, получают равенство
После умножения обеих частей на приращение аргумента Δx, образуется тождество:
в котором в правой части записано слагаемое, являющееся бесконечно малой одного порядка с Δx, далее идет слагаемое более высокого порядка.
Определение 1
Дифференциалом функции y = f (x) первого порядка называется главная часть её приращения f′(x)Δx, которую обозначают dy (или d(f(x)).
Для наглядного представления и понимания определения рассматривается касательная к графику функции y = f(x) в точке x. Когда значение переменной сдвигается по построенной прямой (получает приращение) на некоторую малую величину Δx, значение второй координаты точки тоже меняется.
Значит, дифференциал функции y = f(x) в точке x равен приращению ординаты касательной, когда её абсцисса меняется на величину Δx.
Определение 2
Дифференциал от дифференциала называется дифференциалом второго порядка. Таким же рекуррентным образом вводятся понятия дифференциалов более высоких порядков.
Формы записи дифференциала
Для нахождения дифференциала независимой переменной рассматривают функцию y = x, учитывая, что x’ = 1, а, следовательно:
Отсюда получается формула:
Для второго порядка вводится обозначение d 2 y.
Свойства дифференциала
Существующая таблица производных помогает выделить некоторые свойства дифференциалов, например, для суммы, произведения, частного получаются следующие правила:
Одним из важных свойств является инвариантность (неизменность) формы записи, независимо от того, является ли функция элементарной или композицией элементарных (сложной). Фактически,
Примеры решения задач
Задача №1
Найти дифференциал функции
Задача №2
Вычислить значение дифференциала функции
В помощь студентам создан онлайн калькулятор, который позволяет ввести функцию, нажать кнопку и получить форму или значение дифференциала.
Если dx есть константа, то для высших порядков имеет место следующая формула:
Этот результат вытекает непосредственно из определения:
Задача №3
Найти d 2 y, если y = cos2x и x – независимая переменная.
Если x – функция от некоторой другой независимой переменной, то свойство инвариантности перестаёт работать, следовательно,
Задача №4
Найти d 2 y, если y = x 2 и x = t 3 + 1, t – независимый аргумент.
Нетрудно заметить, что если выразить y напрямую через t, то получится тот же результат.
с высокой степенью точности можно вычислить приращение любой дифференцируемой зависимости.
Раскрыв Δy, сделав соответствующие преобразования, приходят к формуле приближённых вычислений:
Задача №5
Вычислить приближённо arctg1,05.
Пусть f(x) = arctg x. Тогда
Полный дифференциал функции
Математика не ограничивается множеством функций одного независимого аргумента. Рассматриваются зависимости от двух и более переменных.
Определения похожи, отличается вид главной части. Рассматриваются несколько слагаемых.
Например, если z = f(x;y) то
Последнее равенство есть формула полного дифференциала. Для функции нескольких переменных сохраняется принцип построения.
Если рассматривают приращения только по одной переменной, то приходят к понятию частных дифференциалов.
Заключение
Высшая математика позволяет находить приближённо общий корень системы уравнений, пользуясь дифференциальным исчислением, делать прикидку результатов, прогнозировать получаемое.
 mishin05
mishin05
У ДВУХ математических действий дифференцирования: по частному и по полному дифференциалам
должны быть и ДВА обратных действия интегрирования: с константой интегрирования и без константы!
В выше указанной статье я давал выдержку из работы Эйлера: «Интегральное исчисление». Сейчас я еще раз дам отрывок из этой выдержки:
Бедолага Эйлер в обеих своих работах о дифференциальном исчислении и об интегральном исчислении постоянно твердит о том, что дифференциалы не могут быть отличными от нуля, иначе их отношение не даст производную!
Но люди с особым специфическим состоянием мозга не могут понять как может существовать мир без пустых множеств и бесконечностей. Этот мир видится им не таким красочным, как рисуется в их воображаемых моделях.
Я давал в статье Необратимая деградация разума или почему дебилы победили Леонарда Эйлера формулу для получения призводной одной из степенных функций с нулем к которому стремится приращение аргумента. Ноль в этом случае означает отсутствие разницы между двумя значениями.
В статье Секта совреманных «математиков» я показал другую формулу, без нулей, которая подробно показывает как два значения аргумента становятся одним произвольным значением.
Но люди со специфическим состоянием мозга не приемлют отсутствие некоей малой величины, которую они обозначают различными буковками и которая позволяет им утверждать о некоем бесконечном числе слагаемых при интегрировании и некоей степени малости при дифференцировании.
Кто же прав? Леонард Эйлер или толпа современных «математиков»? Можно привести пример из современных учебников, где стремление к нулю разницы между двумя значениями аргумента на графике функции рассматривается как превращение секущей в касательную к линии графика функции. Пока на графике две точки, то значение производной найти невозможно. Как только обе точки сливаются в одну, то тут же сразу появляется производная со своим определенным значением.
Я не понимаю как можно глядеть в книгу и видеть фигу? Ведь пока приращение между двумя значениями аргумента не стало равным нулю, ни о какой производной речи не шло. Как только появилось значение производной, то это означает. что два значения аргумента стали одним и тем же.
Бессмысленно посещать дурку для того, чтобы убеждать пациентов в том, что они зря отрезают себе языки, суют пальцы в розетки или бьются головами о стенки. Я уже понял, что как только некая критическая масса населения получает некий вывих мозга, то процесс уже необратим.
Наверное, именно для такой ситуации природой придумана война. Чтобы нивелировать это фатальное для цивилизации соотношение.
 mishin05
mishin05
У ДВУХ математических действий дифференцирования: по частному и по полному дифференциалам
должны быть и ДВА обратных действия интегрирования: с константой интегрирования и без константы!
Еще раз. Сами по себе это две самостоятельные функции. Но, при использозовании действия «дифференцирования», одна из этих функций станет структурным элементом другой функции. Для чего это нужно? Для адекватного описания действительности. Потому, что почти все объекты действительного мира меняют свои размеры именно интегрированием.
Схематичный пример действий дифференцирования и интегрирования расположен на рисунке в начале статьи.
То есть, на точку «надеваем» колечко на том же самом расстоянии, что и радиус самого колечка, потому, что мы интегируем площади колечек именно по дифференциалу длины того отезка, который называется радиусом. Надеваем все больше колечек, выполняя исходное обязательное условие: Радиус каждого очень тонкого колечка равен расстоянию от первоначальной точки (вершины «пирамидки») до этого колечка. Будем получать объем пирамидки, равный интегралу площади колечек по диференциалу радиуса. Я, надеюсь, схема понятна. Именно эта модель вынесена в заголовок моего блога.
Теперь, вернемся к заявленной теме статьи. Что такое неопределенность «ноль, деленный на ноль» или что такое бесконечность? Это модели нашего разума, а не модели реальности. Если часть площади круга представить как кольцо, ограниченное внутренней окружностью и внешней, то площадь кольца и будет приращением функции площади круга. Расстояние можду этими двумя окружностями и будет приращением аргумента.
Если площадь кольца начать мысленно сжимать, то есть устремить друг к другу внешнюю окружность к внутренней, то пределом площади такого кольца станут две окружности, расположенные рядом. То есть, между ними не «влезет» другая окружность. Это будет элементарное приращение площади круга. Что с радиусом? Его длина станет элементарной и будет находиться между двумя соседними точками. Это и будет элементарным приращением аргумента.
Дифференциал (математика)
Дифференциал — это математический термин, обозначающий некое бесконечно малое приращение.
Содержание
[править] Дифференциал функции
Дифференциал функции равен произведению производной функции на дифференциал аргумента.
Нахождение дифференциала функции называется дифференцированием, так как требует нахождения производной.
[править] Свойства дифференциалов
Для функций u = f(x) и v = g(x) верны правила:
[math]d[f(x)+g(x)]=df(x)+dg(x) \qquad \qquad \qquad \ d[u+v]=du+dv[/math] [math]d[f(x)-g(x)]=df(x)-dg(x) \qquad \qquad \qquad \ d[u-v]=du-dv[/math] [math]d[f(x)\cdot g(x)]=df(x)\cdot g(x)+f(x)\cdot dg(x) \Leftrightarrow \ d[uv]=du\cdot v+u\cdot dv[/math] [math]d\left[\frac
При f(x) и g(x) = C получаем:
[math]d[f(x)+C]=df(x) \qquad \ \ d[u+C]=du[/math] [math]d[f(x)-C]=df(x) \qquad \ \ d[u-C]=du[/math] [math]d[f(x)\cdot C]=C\cdot df(x) \Leftrightarrow \ d[u\cdot C]=C\cdot du[/math] [math]d\left[\frac
При f(x) = C и g(x) получаем:
[math]d[C+g(x)]=dg(x) \qquad \ \ d[C+v]=dv[/math] [math]d[C-g(x)]=dg(x) \qquad \ \ d[C-v]=-dv[/math] [math]d[C\cdot g(x)]=C\cdot dg(x) \Leftrightarrow \ d[C\cdot v]=C\cdot dv[/math] [math]d\left[\frac
[править] Виды дифференциалов:
Дифференциалы элементарных функций — это дифференциалы (табличные) от элементарных функций.
Дифференциалы сложных функций — это дифференциалы от функций, состоящих из внешней функции и внутренней функции (функция от функции).
Формулы дифференциалов сложных функций

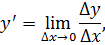
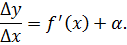
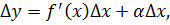

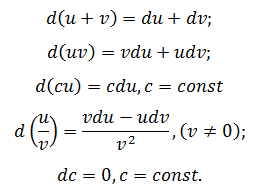

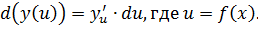
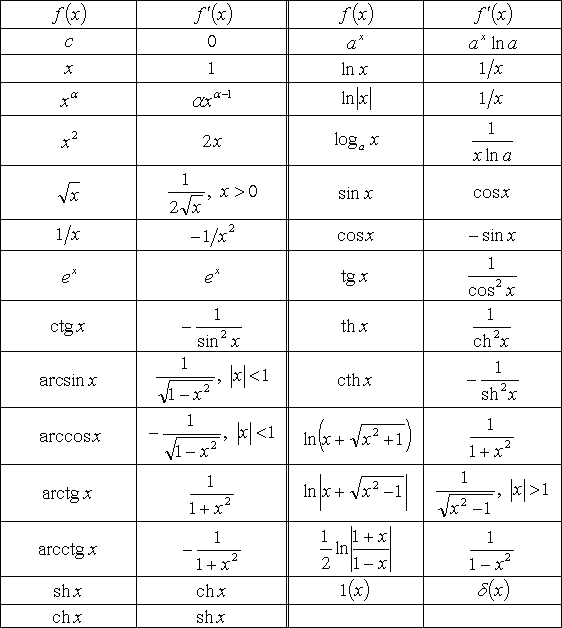
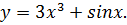
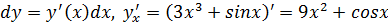
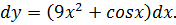
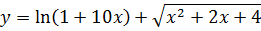
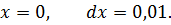
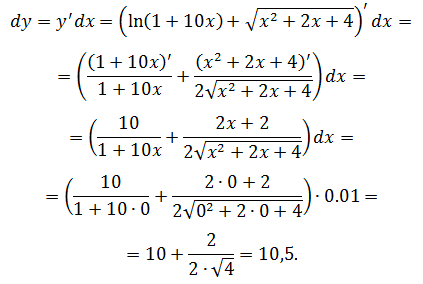
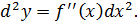
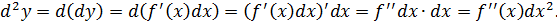

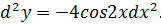
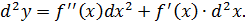
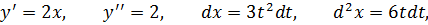
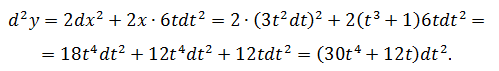
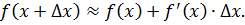
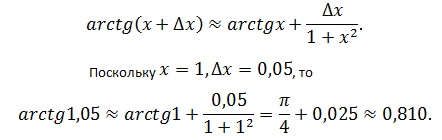


 mishin05
mishin05


