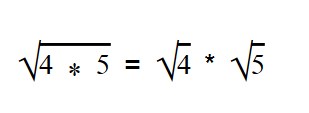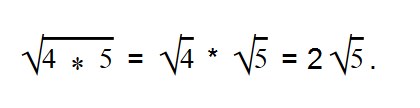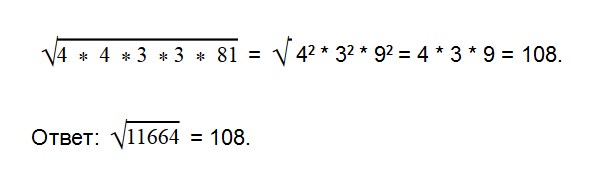зачем число возводят в квадрат

Свойства степеней. Действия со степенями

Что такое степень числа

В учебниках по математике можно встретить такое определение:

«Степенью n числа а является произведение множителей величиной а n-раз подряд»

a — основание степени

n — показатель степени

Соответственно, a n = a·a·a·a. ·a

Читается такое выражение, как a в степени n

Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) на само себя.

А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 — она решается довольно просто:

2 — основание степени

3 — показатель степени

Если вам нужно быстро возвести число в степень, можно использовать наш онлайн-калькулятор. Но чтобы не упасть в грязь лицом на контрольной по математике, придется все-таки разобраться с теорией.

Рассмотрим пример из жизни, чтобы было понятно, для чего можно использовать возведение чисел в степень на практике.

Задачка про миллион: представьте, что у вас есть миллион рублей. В начале каждого года вы зарабатываете на нем еще два. Получается, что миллион каждый год утраивается. Был один, а стало три — и так каждый год. Здорово, правда? А теперь посчитаем, какая сумма у вас будет через 4 года.

Как решаем: один миллион умножаем на три (1·3), затем результат умножаем на три, потом еще на три. Наверное, вам уже стало стало скучно, потому что вы поняли, что три нужно умножить само на себя четыре раза. Так и сделаем:

Математики заскучали и решили все упростить:

Ответ: через четыре года у вас будет 81 миллион.

Таблица степеней

Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3).

Источник

Зачем число возводят в квадрат

Введение.

Математика – очень древняя наука. Многие понятия, правила, законы, формулы уже известны давно, и открыть что-то новое, просто невозможно. Всё равно на уроке математики мы открываем для себя новые знания. Из года в год наши знания увеличиваются. Например, при изучении темы «Степень» узнали, что произведение одинаковых множителей можно записать, как степень данного числа. Так мы познакомились с квадратом и кубом числа.

Устно возводить в квадрат однозначное число легко, для этого надо знать всего лишь таблицу умножения. А как устно возвести в квадрат двузначное число, меня очень заинтересовало.

Умея это выполнять, мы откажемся от письменного умножения. Конечно, можно посмотреть в таблицу квадратов, но она не всегда под руками.

Цель проекта: Поиск приёмов быстрого возведения чисел в квадрат.

Задачи: 1) Познакомиться с историей возникновения степени числа.

2) Изучить приёмы быстрого возведения чисел в квадрат.

3) Вывести свой способ возведения чисел в квадрат.

4) Выбрать из всех самый оптимальный способ.

Гипотеза: Применение приёмов быстрого возведения чисел в квадрат облегчает вычисления, повышает вычислительную культуру учащихся. Возводить в квадрат легко и просто.

Объект исследования: приёмы быстрого возведения чисел в квадрат.

Методы исследования: Анализ литературы. Поисковый метод. Сравнение.

Актуальность проекта: Во все времена умение производить в уме различные вычисления вызывает восхищение, это отличное упражнение, позволяющее поддержать мозг в состоянии «боевой готовности»[1]. Освоение способов устного возведения чисел в квадрат усиливает интерес к математике, развивает внимание, мышление, память, эрудицию и математические способности.

История возникновения квадрата числа.

Сложение, вычитание, умножение и деление идут первыми в списке арифметических действий. У математиков не сразу сложилось представление о возведении в степень как о самостоятельной операции, хотя в самых древних математических текстах Древнего Египта и Междуречья встречаются задачи на вычисление степеней[5].

В своей знаменитой «Арифметике» Диофант Александрийский [2] описывает первые натуральные степени чисел так:

«Все числа… состоят из некоторого количества единиц; ясно, что они продолжаются, увеличиваясь до бесконечности. …среди них находятся: квадраты, получающиеся от умножения не­которого числа самого на себя; это же число называется стороной квадрата, затем кубы, получающиеся от умножения квадратов на их сторону, далее квадрато-квадраты — от умножения квадратов самих на себя, далее квадрато-кубы, получающиеся от умно­жения квадрата на куб его стороны, далее кубо-кубы — от умножения кубов самих на себя».

Прошло много времени и у Рене Декарта[3] в его «Геометрии» (1637) мы находим современное обозначение степеней а?, а. Любопытно, что Декарт считал, что а*а не занимает больше места, чем а 2 и не пользовался этим обозначением при записи произведения двух одинаковых множителей.

Немецкий ученый Лейбниц[4] считал, что упор должен быть сделан на необходимости применения символики для всех записей произведений одинаковых множителей и применял знак а 2 [5].

Приёмы быстрого возведения чисел в квадрат.

Учись считать быстро! Для овладения этим навыком любому человеку нужны:

Давайте познакомимся с некоторыми приёмами возведения в квадрат двузначных чисел, которые выполняются почти мгновенно[1].

Возведение в квадрат числа, оканчивающегося на 5.

Чтобы возвести в квадрат число, оканчивающееся цифрой 5, надо умножить количество его десятков на следующее за ним число и приписать к произведению 25.

Возведение в квадрат числа, первая цифра которого равна 5.

Чтобы возвести в квадрат двузначное число, первая цифра которого равна 5, надо к 25 прибавить число единиц и приписать квадрат числа единиц.

Возведение в квадрат числа, оканчивающегося на 1.

При возведении в квадрат числа, оканчивающегося на 1, нужно округлить число до десятков, возвести новое число в квадрат, и прибавить к этому квадрату исходное число и число, полученное при округлении.

Возведение в квадрат числа, оканчивающегося на 9.

Возведение в квадрат числа, оканчивающегося на 4.

При возведении в квадрат числа, оканчивающегося на 4, нужно заменить цифру 4 на 5, возвести новое число в квадрат и из этого квадрата вычесть исходное число и число, полученное заменой 4 на 5.

Возведение в квадрат числа, оканчивающегося на 6.

При возведении в квадрат числа, оканчивающегося на 6, нужно заменить цифру 6 на 5, возвести новое число в квадрат, и прибавить к этому квадрату исходное число и число, полученное заменой 6 на 5.

Возведение в квадрат числа, близкого к 50.

а) Для чисел от 40 до 50 (числа пятого десятка). Опорное число – 15.

1) 44 2 = (15 + 4) · 100 + (50 – 44) 2 = 1900 + 36 = 1936.

2) 43 2 = 18 · 100 + 7 2 = 1800 + 49 = 1849.

3) 48 2 = 2300 + 4 = 2304.

б) Для чисел от 25 до 40 и до 50. Опорное число – 25.

1) 37 2 = (37 – 25) · 100 + (50 – 37) 2 = 12 · 100 + 13 2 = 1200 + 169 = 1369.

Для этого приёма надо знать квадраты чисел от 1 до 25.

2) 28 2 = 3 · 100 + 22 2 = 300 + 484 = 784.

3) 46 2 = 2100 + 16 = 2116.

4) 39 2 = 1400 + 121 = 1521.

в) Для чисел от 50 до 60 (числа шестого десятка). Опорное число – 25.

1) 57 2 = (25 +7) · 100 + (57 – 50) 2 = 32 · 100 + 7 2 = 3200 + 49 = 3249.

2) 52 2 = 2700 + 4 = 2704.

г) Для чисел от 50 до 60 и до 75. Опорное слово – 25.

Для этого приёма надо знать квадраты чисел от 1 до 25.

1) 58 2 = (58 – 25) · 100 + (58 – 50) 2 = 33 · 100 + 8 2 = 3300 + 64 = 3364.

2) 71 2 = 46 · 100 + 21 2 = 4600 + 441 = 5041.

Возведение в квадрат числа, близкого к 100.

97 2 = (97 – 3) · 100 + 3 2 = 9400 + 9 = 9409, где 3 – дополнение 97 до 100.

94 2 = (94 – 6) · 100 + 6 2 = 8800 + 36 = 8836.

Возведение в квадрат любого двузначного числа.

38 2 = (30 + 8) 2 = (30 + 8) · (30 + 8) = (30 + 8) · 30 + (30 + 8) · 8 = 30 · 30 + 8 · 30 +

+ 30 · 8 + 8 · 8 = 3 · 3 · 100 + 3 · 8 · 10 + 3 · 8 · 10 + 8 · 8 = 3 2 · 100 + 3 · 8 · 2 · 10 + + 8 2 = 9 · 100 + 48 · 10 + 64 = 964 + 480 = 1444.

Можно оформить решение так:

27 2 = 449 + 280 = 729.

84 2 = 6416 + 640 = 7056.

42 2 = 42 · 42 = (42 + 2) · 40 + 2 2 = 44 · 40 + 4 = 1760 + 4 = 1764

78 2 = (78 + 8) · 70 + 64 = 86 · 70 + 64 = 6020 + 64 = 6084.

в) Метод «округления».

1) Для чисел, у которых цифра единиц больше 5:

47 2 = 47 · 47 = 50 · (47 – 3) + 3 2 = 50 · 44 + 9 = 2200 + 9 = 2209.

26 2 = 30 · 22 + 16 = 660 + 16 = 676.

1) Для чисел, у которых цифра единиц меньше 5:

73 2 = 73 · 73 = 70 · (73 + 3) + 3 2 = 70 · 76 + 9 = 5320 + 9 = 5329.

82 2 = 80 · 84 + 4 = 6720 + 4 = 6724.

г) Метод замены квадрата числа произведением.

29 2 = (29 – 9) · (29 + 9) + 9 2 = 20 · 38 + 81 = 760 + 81 = 841.

86 2 = (86 – 6) · (86 + 6) + 6 2 = 80 · 92 + 36 = 7360 + 36 = 7396.

54 2 = 50 · 58 + 16 = 2900 + 16 = 2916.

д) Метод понижения числа на единицу.

28 2 = (28 – 1) 2 + 28 + (28 – 1) = 27 2 + 28 + 27 = 729 + 55 = 784.

56 2 = 55 2 + 56 + 55 = 3025 + 111 = 3136.

Минус этого приёма в том, что квадрат данного двузначного числа выражаем через квадрат числа на единицу меньше, который надо либо вычислять, либо снова понижать, и так до бесконечности.

Возведение в квадрат любого двузначного числа по методу Алины.

Приёмов возведения двузначных чисел в квадрат много и все они разные. Для каждой группы чисел надо знать своё правило, а удержать все правила в уме иногда невозможно.

Собирая материал для проекта, мне захотелось вывести свой приём быстрого возведения двузначного числа в квадрат.

Очень понравился приём возведения в квадрат чисел, оканчивающихся на 5. Он быстрый и понятный. А можно ли этот приём применить для любого числа? Изучая литературу, я нигде этого способа не увидела. Применяя его для любых двузначных чисел, вот что у меня получилось.

Напомню: 35 2 = 3 · (3 + 1) · 100 + 5 2 = 1200 + 25 = 1225.

Возведём по этому способу в квадрат число 36.

Мы знаем, что 36 2 = 1296.

3 · (3 + 1) · 100 + 6 2 = 1200 + 36 = 1236, но 1236 1296. Число 1236 2 = 3 · 4 · 100 + 6 2 + 30 · 2 = 1236 + 60 = 1296.

Рассмотрим другие примеры.

56 2 = 5 · 6 · 100 + 6 2 + 50 · 2 = 3000 + 36 + 100 = 3036 + 100 = 3136.

46 2 = 2036 + 40 · 2 = 2036 + 80 = 2116.

Я много раз возводила числа в квадрат и увидела такую закономерность:

Пусть, например, надо возвести в квадрат число 39. Цифра 9 стоит на четвёртом месте от цифры 5, число 4 удваиваем, это будет 8, а теперь применяем приём:

39 2 = 3 · 4 · 100 + 9 2 + 30 · 8 = 1200 + 81 + 240 = 1281 + 240 = 1521.

240 можно представить так: 30 · 2 · 4, то есть десятки числа удвоить и умножить на номер места цифры единиц от цифры 5.

73 2 = 5609 – применяя приём возведения в квадрат для числа, оканчивающегося на 5. Но 5329 ≠ 5609.

х = 280, где 280 = 70 · 2 · 2, первая двойка удваивает число десятков в числе; вторая двойка обозначает номер места цифры 3 от цифры 5.

Эврика! Способ найден!

73 2 = 7 · 8 ·100 + 3 · 3 – 70 · 2 · 2 = 5609 – 280 = 5329.

Можно оформить решение и так:

Какой приём возведения двузначного числа в квадрат наиболее простой? Для себя я выбрала два приёма. Мне они оба понятные и несложные.

Какой приём выберите вы, думайте сами. Вам решать.

Заключение.

Владение приёмами быстрого возведения двузначного числа в квадрат даёт возможность выбрать в каждом отдельном случае наиболее рациональные и эффективные пути вычислений, что приводит:

Считаю, что возводить двузначные числа в квадрат легко и просто. Гипотеза доказана.

Умение считать в уме остаётся полезным навыком для современного человека, несмотря на то, что он владеет всевозможными устройствами, способными считать за него.

Возможность обходиться без калькулятора и в нужный момент оперативно решить поставленную арифметическую задачу – это здорово[1]!

Источник

Что такое квадратный корень

Что такое квадратный корень

Определение арифметического квадратного корня ясности не добавляет, но заучить его стоит:

Арифметическим квадратным корнем из неотрицательного числа a называется такое неотрицательное число, квадрат которого равен a.

Определение квадратного корня также можно представить в виде формул:
√a = x
x 2 = a
x ≥ 0
a ≥ 0

Из определения следует, что a не может быть отрицательным числом. То есть то, что стоит под корнем — обязательно положительное число.

Чтобы разобраться, почему именно так и никак иначе, давайте рассмотрим пример.

Попробуем найти корень из √-16

Здесь логично предположить, что 4, но давайте проверим: 4*4 = 16 — не сходится.

Получается, что ни одно число не может дать отрицательный результат при возведении его в квадрат.

Числа, стоящие под знаком корня, должны быть положительными.

Исходя из определения, значение корня также не должно быть отрицательным.

Разница между квадратным корнем и арифметическим квадратным уравнением

Прежде всего, чтобы разграничить эти два понятия, запомните:

Это два нетождественных друг другу выражения.

Из выражения x 2 = 16 следует, что:

Если две вертикальные палочки возле x вводят вас в замешательство, почитайте нашу статью о модуле числа.

В то же самое время, из выражения x = √16 следует, что x = 4.

Если ситуация все еще кажется запутанной и нелогичной, просто запомните, что отрицательное число может быть решением только в квадратном уравнении. Если в решении «минус» — есть два варианта:

Если вы извлекаете квадратный корень из числа, то можете быть уверены, вас ждет «положительный» результат.

Давайте рассмотрим пример, чтобы окончательно выяснить разницу между квадратным корнем и квадратным уравнением.

Даны два выражения:

Первое выражение — квадратное уравнение.

Второе выражение — арифметический квадратный корень.

Мы видим, что результатом решения первого выражения стали два числа — отрицательное и положительное. А во втором случае — только положительное.

Запись иррациональных чисел с помощью квадратного корня

Иррациональное число — это число, которое нельзя представить в виде обыкновенной дроби.

Чаще всего, иррациональные числа можно встретить в виде корней, логарифмов, степеней и т.д.

Примеры иррациональных чисел:

Чтобы упростить запись иррациональных чисел, математики ввели понятие квадратного корня. Давайте разберем пару примеров, чтобы увидеть квадратный корень в деле.

Дано уравнение: x 2 = 2.

Сразу сталкиваемся с проблемой, поскольку очевидно, что ни одно целое число не подходит.

Переберем числа, чтобы удостовериться в этом:

1 * 1 = 1,
2 * 2 = 4,
3 * 3 = 9.

Отрицательные числа дают такой же результат. Значит результатом решения не могут быть целые числа.

Извлечение корней

Решать примеры с квадратными корнями намного легче, если запомнить как можно больше квадратов чисел. Для этого воспользуйтесь таблицей — сохраните ее себе и используйте для решения задачек.

Таблица квадратов

Вот несколько примеров извлечения корней, чтобы научиться пользоваться таблицей:

Ищем в таблице число 289, двигаемся от него влево и вверх, чтобы определить цифры, образующие нужное нам число.

Ищем в таблице число 3025.
Влево — 5, вверх — 5.

Ищем в таблице число 7396.

Ищем в таблице число 9025.

Ищем в таблице число 1600.

Извлечением корня называется нахождение его значение.

Свойства арифметического квадратного корня

У арифметического квадратного корня есть 3 свойства — их нужно запомнить, чтобы проще решать примеры.

Давайте потренируемся и порешаем примеры на все три операции с корнями. Не забывайте обращаться к таблице квадратов. Попробуйте решить примеры самостоятельно, а для проверки обращайтесь к ответам.

Умножение арифметических корней

Для умножения арифметических корней используйте формулу:

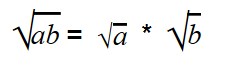Примеры:

Внимательно посмотрите на второе выражение и запомните, как записываются такие примеры.

Если нет возможности извлечь корни из чисел, то поступаем так:

Деление арифметических корней

Для деления арифметических корней используйте формулу:

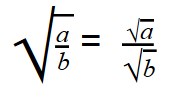Примеры:

Выполняя деление, не забывайте сокращать множители. При делении арифметических корней, используйте правила преобразования обыкновенных дробей.

Возведение арифметических корней в степень

Для возведения арифметического корня в степень используйте формулу:

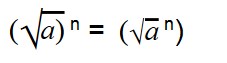Примеры:

Эти две формулы нужно запомнить:

Повторите свойства степеней, чтобы без труда решать такие примеры.

Внесение множителя под знак корня

Вы уже умеете по-всякому крутить и вертеть квадратными корнями: умножать, делить, возводить в степень. Богатый арсенал, не правда ли? Осталось овладеть еще парой приемов и можно без страха браться за любую задачку.

А теперь давайте разберемся, как вносить множитель под знак корня.

Число семь умножено на квадратный корень из числа девять.

Извлечем квадратный корень и умножим его на 7.

В данном выражение число 7 — множитель. Давайте внесем его под знак корня.

Запомните, что вносить множитель под знак корня обязательно нужно так, чтобы значение исходного выражения осталось неизменным. Иными словами, после наших манипуляций с корнем, значение выражения должно по-прежнему оставаться 21.

Вы помните, что (√a) 2 = a

Тогда число 7 должно быть возведено во вторую степень. В этом случае значение выражения останется тем же.

7√9 = √7 2 * 9 = √49 * 9 = √49 * √9 = 7 * 3 = 21.

Формула внесения множителя под знак корня:

Потренируемся вносить множители. Попробуйте решить примеры самостоятельно, сверяясь с ответами.

Вынесение множителя из-под знака корня

С тем, как вносить множитель под корень мы, кажется, разобрались. Но алгебра — такая алгебра, поэтому теперь неплохо бы и вынести множитель из-под знака корня.

Дано выражение в виде квадратного корня из произведения.

Вы уже наверняка без труда извлекаете квадратный корень из чего угодно, поэтому знаете, что делать.

Извлекаем корень из всех имеющихся множителей.

В данном выражении квадратный корень мы можем извлечь только из 4, поэтому:

Таким образом множитель выносится из-под знака корня.

Давайте разберем примеры. Попробуйте вынести множители из-под знака корня самостоятельно, сверяясь с ответами.

Раскладываем подкоренное выражение на множители 28 = 7*4.

Сравнение квадратных корней

Мы почти досконально разобрали арифметический квадратный корень, научились умножать, делить и возводить его в степень. Теперь вы без труда можете вносить множители под знак корня и выносить их оттуда. Осталось научиться сравнивать корни и стать непобедимым теоретиком.

Итак, чтобы понять, как сравнить два квадратных корня, нужно запомнить пару правил.

Если:

Потренируйтесь в сравнении корней. Сверяете свои результаты с ответами.

Ответ: преобразовываем выражение 9√5.

9√5 = √81 * √5 = √81*5 = √405

Ответ: преобразовываем выражение 7√12.

7√12 = √49 * √12 = √49*12 = √588

Это значит, что 7√12 > √20.

Как видите, ничего сложного в сравнении арифметических квадратных корней нет.

Самое главное — выучить формулы и сверяться с таблицей квадратов, если значения корня слишком большие для легкого вычисления в уме.

Не бойтесь пользоваться вспомогательными материалами. Математика просто создана для того, чтобы окружить себя подсказками и намеками.

Когда вы почувствуете, что уже достаточно натренировались в решении примеров с квадратными корнями, можете позволить себе время от времени прибегать к помощи онлайн-калькуляторов. Они помогут решать примеры быстрее и быть эффективнее.

Таких калькуляторов в интернете много, вот один из них.

Извлечение квадратного корня из большого числа

Вы уже наверняка познакомились и подружились с таблицей квадратов. Она — ваша правая рука. С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.

Но, как вы можете заметить, таблица заканчивается на числе 9801. А это, согласитесь, не самое крупное число из тех, что могут вам попасться в примере.

Чтобы извлечь корень из большого числа, которое отсутствует в таблице квадратов, нужно:

Извлечь корень из большого числа можно разными способами — вот один из них.

Извлечем корень из √2116.

Наша задача в том, чтобы определить между какими десятками стоит число 2116.

Мы видим что, 2116 больше 1600, но меньше 2500.

41, 42, 43, 44, 45, 46, 47, 48, 49.

Запомните лайфхак по вычислению всего на свете, что нужно возвести в квадрат.

Не секрет, что на последнем месте в любом числе может стоять только одна цифра от 1 до 0.

Как пользоваться таблицей

4 2 = 16 ⇒ 6

5 2 = 25 ⇒ 5

6 2 = 36 ⇒ 6

7 2 = 49 ⇒ 9

8 2 = 64 ⇒ 4

9 2 = 81 ⇒ 1

Мы знаем, что число 41, возведенное в квадрат, даст число, на конце которого — цифра 1.

Число, 42, возведенное в квадрат, даст число, на конце которого — цифра 4.

Число 43, возведенное в квадрат, даст число, на конце которого — 9.

Такая закономерность позволяет нам без записи «перебрать» все возможные варианты, исключая те, которые не дают нужную нам цифру 6 на конце.

Далее вычисляем: 44 * 44 = 1936.

Если такой способ показался не до конца понятным — можно потратить чуть больше времени и разложить число на множители. Если решить все правильно, получим такой же результат.

Еще пример. Извлечем корень из числа √11664

Разложим число 11664 на множители:

Запишем выражение в следующем виде:

Извлечь квадратный корень из большого числа гораздо проще с помощью калькулятора. Но знать парочку таких способов «на экстренный случай» точно не повредит. Например, для контрольной или ЕГЭ.

Чтобы закрепить все теоретические знания, давайте ещё немного поупражняемся в решении примеров на арифметические квадратные корни.

109004, Москва, ул. Александра Солженицына, 23а, строение 1, подъезд 10

Источник