принцип метода обучения с учителем

Все модели машинного обучения за 5 минут

Mar 6, 2020 · 5 min read

Фундаментальная сегментация моделей машинного обучения

Все модели машинного обучения разделяются на обучение с учителем (supervised) и без учителя (unsupervised). В первую категорию входят регрессионная и классификационная модели. Рассмотрим значения этих терминов и входящие в эти категории модели.

Обучение с учителем

Представляет собой изучение функции, которая преобразует входные данные в выходные на основе примеров пар ввода-вывода.

Например, из набора данных с двумя переменными: возраст (входные данные) и рост (выходные данные), можно реализовать модель обучения для прогнозирования роста человека на основе его возраста.

Пример обучения с учителем

Повторюсь, обучение с учителем подразделяется на две подкатегории: регрессия и классификация.

Регрессия

В регре с сионных моделях вывод является непрерывным. Ниже приведены некоторые из наиболее распространенных типов регрессионных моделей.

Линейная регрессия

Пример линейной регрессии

Задача линейной регрессии заключается в нахождении линии, которая наилучшим образом соответствует данным. Расширения линейной регрессии включают множественную линейную регрессию (например, поиск наиболее подходящей плоскости) и полиномиальную регрессию (например, поиск наиболее подходящей кривой).

Дерево решений

Изображение из Kaggle

Дерево решений — популярная модель, используемая в исследовании операций, стратегическом планировании и машинном обучении. Каждый прямоугольник выше называется узлом. Чем больше узлов, тем более точным будет дерево решений. Последние узлы, в которых принимается решение, называются листьями дерева. Деревья решений интуитивны и просты в создании, однако не предоставляют точные результаты.

Случайный лес

Случайный лес — это техника ансамбля методов, основанная на деревьях решений. Случайные леса включают создание нескольких деревьев решений с использованием первоначальных наборов данных и случайный выбор поднабора переменных на каждом этапе. Затем модель выбирает моду (значение, которое встречается чаще других) из всех прогнозов каждого дерева решений. Какой в этом смысл? Модель “победы большинства” снижает риск ошибки отдельного дерева.

Например, у нас есть одно дерево решений (третье), которое предсказывает 0. Однако если полагаться на моду всех 4 деревьев, прогнозируемое значение будет равно 1. В этом заключается преимущество случайных лесов.

Нейронная сеть

Визуальное представление нейронной сети

Нейронная сеть — это многослойная модель, устроенная по системе человеческого мозга. Как и нейроны в нашем мозге, круги выше представляют узлы. Синим обозначен слой входных данных, черным — скрытые слои, а зеленым — слой выходных данных. Каждый узел в скрытых слоях представляет функцию, через которую проходят входные данные, приводящие к выходу в зеленых кругах.

Классификация

В классификационных моделях вывод является дискретным. Ниже приведены некоторые из наиболее распространенных типов классификационных моделей.

Логистическая регрессия

Логистическая регрессия аналогична линейной регрессии, но используется для моделирования вероятности ограниченного числа результатов, обычно двух. Логистическое уравнение создается таким образом, что выходные значения могут находиться только между 0 и 1:

Метод опорных векторов

Метод опорных векторов — это классификационный метод обучения с учителем, довольно сложный, но достаточно интуитивный на базовом уровне.

Предположим, что существует два класса данных. Метод опорных векторов находит гиперплоскость или границу между двумя классами данных, которая максимизирует разницу между двумя классами. Есть множество плоскостей, которые могут разделить два класса, но только одна из них максимизирует разницу или расстояние между классами.

Наивный Байес

Наивный Байес — еще один популярный классификатор, используемый в науке о данных. Его идея лежит в основе теоремы Байеса:

Несмотря на ряд нереалистичных предположений, сделанных в отношении наивного Байеса (отсюда и название “наивный”), он не только доказал свою эффективность в большинстве случаев, но и относительно прост в построении.

Обучение без учителя

В отличие от обучения с учителем, обучение без учителя используется для того, чтобы сделать выводы и найти шаблоны из входных данных без отсылок на помеченные результаты. Два основных метода, используемых в обучении без учителя, включают кластеризацию и снижение размерности.

Кластеризация

Кластеризация — это техника обучения без учителя, которая включает в себя группирование или кластеризацию точек данных. Чаще всего она используется для сегментации потребителей, выявления мошенничества и классификации документов.

Распространенные методы кластеризации включают кластеризацию с помощью k-средних, иерархическую кластеризацию, сдвиг среднего значения и кластеризацию на основе плотности. У каждого из них есть свой способ поиска кластеров, однако все они предназначены для достижения одного результата.

Понижение размерности

Снижение размерности — это процесс уменьшения числа рассматриваемых случайных переменных путем получения набора главных переменных. Проще говоря, это процесс уменьшения размера набора признаков (уменьшение количества признаков). Большинство методов снижения размерности могут быть классифицированы как отбор или извлечение признаков.

Популярный метод понижения размерности называется методом главных компонент (PCA). Он представляет собой проецирование многомерных данных (например, 3 измерения) в меньшее пространство (например, 2 измерения). Это приводит к уменьшению размерности данных (2 измерения вместо 3) при сохранении всех исходных переменных в модели.

Источник

Риски и предостережения при применении метода главных компонент к задачам обучения с учителем

Пространство высокой размерности и его проклятие

Проклятие размерности – это серьезная проблема при работе с реальными наборами данных, которые, как правило, являются многомерными. По мере увеличения размерности пространства признаков число конфигураций может расти экспоненциально, и, по итогу число конфигураций, охватываемых наблюдением, уменьшается.

В таком случае метод главных компонент (PCA) будет играть важную роль, эффективно понижая размерность данных и сохраняя при этом как можно больше вариаций, присутствующих в наборе данных.

Давайте вкратце рассмотрим суть метода главных компонент, прежде чем углубляться в проблему.

Метод Главных Компонент – определение

Основная идея метода главных компонент заключается в том, чтобы уменьшить размерность набора данных, состоящего из большого количества взаимосвязанных переменных, сохраняя при этом максимальное разнообразие, присутствующее в наборе данных.

Определим симметричную матрицу А,

Где Х – матрица m x n независимых переменных, где m – число столбцов, а n – число точек данных. Матрицу А можно разложить следующим образом:

Где D – диагональная матрица, а E — матрица собственных векторов А, расположенных столбцами.

Почему бездумное применение метода главных компонент является проклятием для задач обучения с учителем?

В литературе часто упоминается использование метода главных компонент в регрессии, а также в задачах мультиколлинеарности. Однако наряду с использованием регрессии на главных компонентах, было много неверных представлений про объяснимость переменной отклика главными компонентами и порядок их важности.

Распространенное заблуждение, которое встречалось несколько раз в различных статьях и книгах, гласит, что в среде обучения с учителем при регрессии на главных компонентах, главные компоненты независимой переменной с маленькими собственными значениями, не будут играть важной роли в объяснении переменной отклика, что приводит нас к цели написания этой статьи. Идея состоит в том, что компоненты с маленькими собственными значениями могут быть столь же важны или даже гораздо более важны, чем основные компоненты с большими собственными значениями при объяснении переменной отклика.

Ниже я перечислю несколько примеров публикаций, о которых я говорил:

[1]. Мэнсфилд и др. (1977, стр. 38) предполагает, что если удаляются только компоненты с небольшой дисперсией, то регрессия не сильно теряет в прогностической способности.
[2]. В книге Ганста и Мейсона (1980) 12 страниц посвящены регрессии на главных компонентах, и большая часть дискуссии предполагает, что удаление главных компонент основано исключительно на их дисперсиях. (стр. 327–328).
[3]. Мостеллер и Тьюрки (1977, стр. 397–398) также аргументируют, что компоненты с небольшой дисперсией вряд ли будут важны в регрессии, очевидно, тем, что природа «хитра», но не «единообразна».
[4]. Хокинг (1976, стр. 31) еще жестче определяет правило сохранения главных компонент в регрессии, основываясь на дисперсии.

Теоретическое объяснение и понимание

Для начала давайте получим корректное математическое обоснование вышеупомянутой гипотезы, а затем дадим небольшие пояснения для лучшего понимания с помощью геометрической визуализации и моделирования.

Допустим,
Y – переменная отклика,
X – Матрица пространства признаков
Z – Стандартизованная версия Х

Пускай …. ≥ λp$» data-tex=»inline»/> будут собственными значениями Z T Z (корреляционной матрицы), а V – соответствующими собственными векторами, тогда в W=ZV, столбцы в W будут представлять главные компоненты Z. Стандартный метод, применяемый при регрессии на главных компонентах, заключается в регрессии первых m главных компонент на Y, и задачу можно представить через теорему ниже и ее пояснение [2].

Теорема:

Пусть W= (W₁,…,Wp) – собственные вектора Х. Теперь рассмотрим регрессионную модель:

Если истинный вектор коэффициентов регрессии β сонаправлен с j-м собственным вектором Z T Z, то при регрессии Y на W, j-й главный компонент Wⱼ будет вносить вклад в обучение, тогда как оставшиеся не будут вносить вклада в принципе.

Доказательство: Пусть V=(V₁,…,Vp) – матрица собственных векторов Z T Z. Тогда

Так как , где коэффициенты регрессии выражения.

Если β сонаправлен с j-м собственным вектором Vⱼ, тогда Vⱼ = aβ, где a – ненулевое скалярное значение. Следовательно, θj = Vⱼᵀβ = aβᵀβ и θᴋ = Vᴋᵀβ = 0, где k≠j. Таким образом коэффициент регрессии θᴋ соответствующий Wᴋ равен нулю, при k≠j, соответственно,

Поскольку переменная Wᴋ не уменьшает сумму квадратов, если ее коэффициент регрессии равен 0, то Wj принесет основной вклад, в то время как остальные главные компоненты не внесут никакого вклада.

Геометрическое значение и моделирование

А теперь давайте смоделируем и получим геометрическое представление вышеперечисленных математических выкладок. Объяснение проиллюстрировано с помощью моделирования двумерного пространства признаков (Х) и одной переменной отклика, чтобы гипотезу можно было легко понять визуально.

Рисунок 1: Одномерные и двумерные графики для рассматриваемых переменных Х1 и Х2

На первом этапе моделирования пространство признаков было смоделировано с помощью многомерного нормального распределения с очень высокой корреляцией между переменными и главными компонентами.

Рисунок 2: Тепловая карта корреляции для PC1 и PC2 (главных компонент)

Из графика очень хорошо видно, что между главными компонентами нет никакой корреляции. На втором шаге происходит моделирование значений переменной отклика Y таким образом, чтобы направление коэффициента Y главных компонент совпадало с направлением второй главной компоненты.

После получения переменной отклика, корреляционная матрица будет выглядеть примерно следующим образом.

Рисунок 3: Тепловая карта для переменной Y и PC1 и PC2.

На графике хорошо видно, что между Y и PC2 корреляция выше, чем между Y и PC1, что подтверждает нашу гипотезу.

Рисунок 4: Дисперсия пространства признаков, объясняемая PC1 и PC2.

Поскольку на рисунке показано, что PC1 объясняет 95% дисперсии Х, то по логике, изложенной выше, мы должны полностью игнорировать PC2 при регрессии.

Так давайте же последуем ей и увидим, что получится!

Рисунок 5. Результат регрессии с Y и PC1.

Таким образом R², равный 0, говорит о том, что несмотря на то, что PC1 дает 95% дисперсии Х, она все еще не объясняет переменную отклика.

Теперь сделаем то же самое с PC2, которая объясняет лишь 5% дисперсии Х, и посмотрим, что из этого выйдет.

Рисунок 6: Результат регрессии с Y и PC2.

Юху! Вы только посмотрите, что произошло: главная компонента, которая объясняла 5% дисперсии Х, дала 72% дисперсии Y. Есть также и реальные примеры в подтверждение таким ситуациям:

[1] Смит и Кэмпбелл (1980) привели пример из химических технологий, где были 9 регрессорных переменных, и когда дисперсия восьмой главной компоненты составляла 0,06% от общей дисперсии, которая была бы не принята в расчет из-за вышеизложенной логики.
[2] Второй пример предоставили нам Кунг и Шариф (1980). В исследовании, посвящённом прогнозированию даты начала муссонов по десяти метеорологическим переменным, значимыми компонентами были только восьмая, вторая и десятая. В этом примере показано, что даже главная компонента с наименьшим собственным значением будет третьей по значимости с точки зрения объяснения изменчивости переменной отклика.

Вывод

Приведенные выше примеры показывают, что нецелесообразно удалять главные компоненты с маленькими собственными значениями, так как они влияют лишь на объяснимость в пространстве признаков, но не переменной отклика. Следовательно, нужно сохранять все компоненты в методах понижении размерности при обучении с учителем, таких как регрессия частично наименьших квадратов и регрессия наименьших углов, о которых мы поговорим в дальнейших статьях.

Узнать подробнее о курсе «Machine Learning. Базовый курс», а также посетить бесплатный урок, можно записавшись на бесплатный вебинар по этой ссылке.

Источник

Обучение с учителем

Материал из MachineLearning.

Обучение с учителем (Supervised learning) — один из разделов машинного обучения, посвященный решению следующей задачи. Имеется множество объектов (ситуаций) и множество возможных ответов (откликов, реакций). Существует некоторая зависимость между ответами и объектами, но она неизвестна. Известна только конечная совокупность прецедентов — пар «объект, ответ», называемая обучающей выборкой. На основе этих данных требуется восстановить зависимость, то есть построить алгоритм, способный для любого объекта выдать достаточно точный ответ. Для измерения точности ответов определённым образом вводится функционал качества.

Под учителем понимается либо сама обучающая выборка, либо тот, кто указал на заданных объектах правильные ответы. Существует также обучение без учителя, когда на объектах выборки ответы не задаются.

Содержание

Типология задач обучения с учителем

Типы входных данных

Типы откликов

Обучение с учителем: формальная постановка

Говорят также, что алгоритм должен обладать способностью к обобщению эмпирических фактов, или выводить общее знание (закономерность, зависимость) из частных фактов (наблюдений, прецедентов).

Данная постановка является обобщением классических задач аппроксимации функций. В классической аппроксимации объектами являются действительные числа или векторы. В реальных прикладных задачах входные данные об объектах могуть быть неполными, неточными, неоднородными, нечисловыми. Эти особенности приводят к большому разнообразию методов обучения с учителем.

Функции потерь и функционалы качества

Типичный выбор функции потерь:

Вводится функционал качества, характеризующий среднюю ошибку (эмпирический риск) алгоритма на произвольной выборке

Метод минимизации эмпирического риска — один из наиболее распространённых подходов к обучению алгоритмов по прецедентам. Он заключается в том, чтобы в заданной модели алгоритмов найти алгоритм, минимизирующий среднюю ошибку на обучающей выборке:

Тем самым задача обучения сводится к оптимизации и может быть решена численными методами оптимизации.

Обобщающая способность и проблема переобучения

Практически в каждом методе предпринимаются специальные усилия, чтобы избежать переобучения. границы применимости метода минимизации эмпирического риска и проблему переобучения изучает теория вычислительного обучения.

Признаковое пространство

В зависимости от множества признаки делятся на следующие типы:

Часто встречаются прикладные задачи с разнотипными признаками, для их решения подходят далеко не все методы.

Примеры прикладных задач

Задачи медицинской диагностики

В роли объектов выступают пациенты. Признаки характеризуют результаты обследований, симптомы заболевания и применявшиеся методы лечения. Примеры бинарных признаков: пол, наличие головной боли, слабости. Порядковый признак — тяжесть состояния (удовлетворительное, средней тяжести, тяжёлое, крайне тяжёлое). Количественные признаки — возраст, пульс, артериальное давление, содержание гемоглобина в крови, доза препарата. Признаковое описание пациента является, по сути дела, формализованной историей болезни. Накопив достаточное количество прецедентов в электронном виде, можно решать различные задачи:

Ценность такого рода систем в том, что они способны мгновенно анализировать и обобщать огромное количество прецедентов — возможность, недоступная специалисту-врачу.

Предсказание месторождений полезных ископаемых

Признаками являются данные геологической разведки. Наличие или отсутствие тех или иных пород на территории района кодируется бинарными признаками. Физико-химические свойства этих пород могут описываться как количественными, так и качественными признаками. Обучающая выборка составляется из прецедентов двух классов: районов известных месторождений и похожих районов, в которых интересующее ископаемое обнаружено не было. При поиске редких полезных ископаемых количество объектов может оказаться намного меньше, чем количество признаков. В этой ситуации плохо работают классические статистические методы. Задача решается путём поиска закономерностей в имеющемся массиве данных. В процессе решения выделяются короткие наборы признаков, обладающие наибольшей информативностью — способностью наилучшим образом разделять классы. По аналогии с медицинской задачей, можно сказать, что отыскиваются «синдромы» месторождений. Это важный побочный результат исследования, представляющий значительный интерес для геофизиков и геологов.

Оценивание кредитоспособности заёмщиков

Эта задача решается банками при выдаче кредитов. Потребность в автоматизации процедуры выдачи кредитов впервые возникла в период бума кредитных карт 60-70-х годов в США и других развитых странах. Объектами в данном случае являются физические или юридические лица, претендующие на получение кредита. В случае физических лиц признаковое описание состоит из анкеты, которую заполняет сам заёмщик, и, возможно, дополнительной информации, которую банк собирает о нём из собственных источников. Примеры бинарных признаков: пол, наличие телефона. Номинальные признаки — место проживания, профессия, работодатель. Порядковые признаки — образование, занимаемая должность. Количественные признаки — сумма кредита, возраст, стаж работы, доход семьи, размер задолженностей в других банках. Обучающая выборка составляется из заёмщиков с известной кредитной историей. В простейшем случае принятие решений сводится к классификации заёмщиков на два класса: «хороших» и «плохих». Кредиты выдаются только заёмщикам первого класса. В более сложном случае оценивается суммарное число баллов (score) заёмщика, набранных по совокупности информативных признаков. Чем выше оценка, тем более надёжным считается заёмщик. Отсюда и название — кредитный скоринг. На стадии обучения производится синтез и отбор информативных признаков и определяется, сколько баллов назначать за каждый признак, чтобы риск принимаемых решений был минимален. Следующая задача — решить, на каких условиях выдавать кредит: определить процентную ставку, срок погашения, и прочие параметры кредитного договора. Эта задача также может быть решения методами обучения по прецедентам.

Прогнозирование потребительского спроса

Решается современными супермаркетами и торговыми розничными сетями. Для эффективного управления торговой сетью необходимо прогнозировать объёмы продаж для каждого товара на заданное число дней вперёд. На основе этих прогнозов осуществляется планирование закупок, управление ассортиментом, формирование ценовой политики, планирование промоакций (рекламных кампаний). Специфика задачи в том, что количество товаров может исчисляться десятками или даже сотнями тысяч. Прогнозирование и принятие решений по каждому товару «вручную» просто немыслимо. Исходными данными для прогнозирования являются временные ряды цен и объёмов продаж по товарам и по отдельным магазинам. Современные технологии позволяют снимать эти данные непосредственно с кассовых аппаратов. Для увеличения точности прогнозов необходимо также учитывать различные внешние факторы, влияющие на потребительский спрос: уровень инфляции, погодные условия, рекламные кампании, социально-демографические условия, активность конкурентов. В зависимости от целей анализа в роли объектов выступают либо товары, либо магазины, либо пары «магазин, товар». Ещё одна особенность задачи — несимметричность функции потерь. Если прогноз делается с целью планирования закупок, то потери от заниженного прогноза существенно выше потерь от завышенного.

Принятие инвестиционных решений на финансовом рынке

Источник

Революция машинного обучения: общие принципы и влияние на SEO

Предлагаю вашему вниманию перевод статьи «Революция машинного обучения» за авторством Эрика Энжа (Eric Enge).

Машинное обучение уже само по себе является серьезной дисциплиной. Оно активно используется вокруг нас, причем в гораздо более серьезных масштабах, чем вы можете себе представить. Несколько месяцев назад я решил углубиться в эту тему, чтобы узнать о ней больше. В этой статье я расскажу о некоторых базовых принципах машинного обучения, а также поделюсь своими рассуждениями по поводу его влияния на SEO и digital-маркетинг.

Для справки, рекомендую посмотреть презентацию Рэнда Фишкина «SEO in a Two Algorithm World», где Рэнд подробно рассматривает влияние машинного обучения на поиск и SEO. К этой теме я еще вернусь.

Я также упомяну сервис, который позволяет спрогнозировать шансы ретвита вашего поста на основании следующих параметров: показатель Followerwonk Social Authority, наличие изображений, хэштегов и некоторых других факторов. Я назвал этот сервис Twitter Engagement Predictor (TEP). Чтобы разработать такую систему мне понадобилось создать и обучить нейронную сеть. Вы указываете исходные параметры твита, сервис обрабатывает их и прогнозирует шансы ретвита.

TEP использует данные исследования, опубликованного в декабре 2014 «Twitter engagement» (вовлечение в Twitter), где мы проанализировали 1,9 миллионов оригинальных твитов (исключая ретвиты и избранное), чтобы определить основные факторы, которые влияют на получение ретвитов.

Мое путешествие в машинное обучение

Свое первое представление о машинном обучении я получил в 2011 году, когда брал интервью у гуглера Питера Норвига, который рассказал мне как с помощью этой технологии Google обучает сервис Google Translate.

Если вкратце, они собирают информацию о всех вариантах перевода слова в сети и на основе этих данных проводят обучение. Это очень серьезный и сложный пример машинного обучения, Google применила его в 2011 году. Стоит сказать, что сегодня все лидеры рынка — например, Google, Microsoft, Apple и Facebook используют машинное обучение для многих интересных направлений.

Еще в ноябре, когда я захотел серьезнее разобраться в этой теме, я приступил к поиску статей в сети. Вскоре я обнаружил отличный курс по машинному обучению на Coursera. Его преподает Andrew Ng (Эндрю Ын) из Стэнфордского университета, курс дает хорошее представление об основах машинного обучения.

Внимание: Курс довольно объемный (19 занятий, каждое в среднем занимает около часа или больше). Он также требует определенного уровня подготовки в области математики, чтобы вникнуть в вычисления. В ходе курса вы погрузитесь в математику с головой. Но суть в следующем: если вы владеете необходимым бэкграундом в математике и полны решимости, то это хорошая возможность пройти бесплатный курс, чтобы усвоить каноны машинного обучения.

Кроме этого, Ын продемонстрирует вам множество примеров на языке Octave. На основе изученного материала вы сможете разработать собственные системы машинного обучения. Именно это я и сделал в примере программы из статьи.

Основные положения машинного обучения

Прежде всего, позвольте прояснить одну вещь: я не являюсь ведущим специалистом в области машинного обучения. Тем не менее, я узнал достаточно, чтобы рассказать вам о некоторых базовых положениях. В машинном обучении можно выделить два основных способа: обучение с учителем и обучение без учителя. Для начала я рассмотрю обучение с учителем.

Машинное обучение с учителем

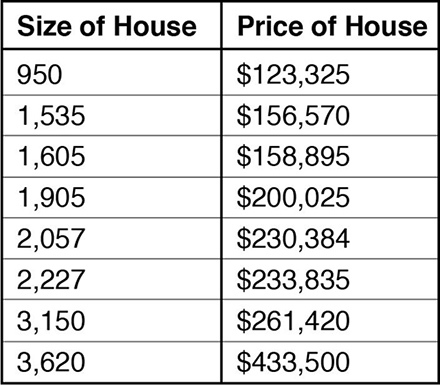
На базовом уровне можно представить обучение с учителем как создание серии уравнений для соответствия известному набору данных. Допустим, вам нужен алгоритм для оценки стоимости недвижимости (этот пример Ын часто использует в курсе Coursera). Возьмем некоторые данные, которые будут выглядеть следующим образом:

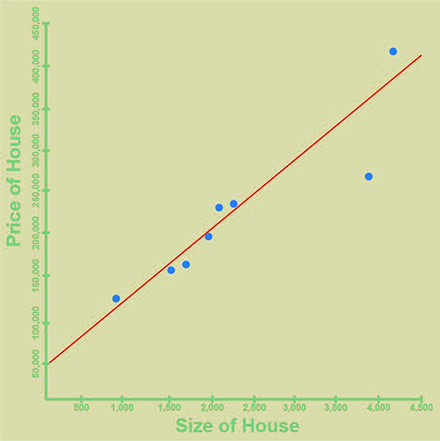
В этом примере у нас есть (вымышленные) исторические данные, которые показывают стоимость дома в зависимости от его размера. Как вы уже могли заметить, чем больше дом, тем дороже он стоит, но эта зависимость не ложится на прямую. Тем не менее, мы можем вычислить такую прямую, которая довольно неплохо будет соответствовать исходным значениям, она будет выглядеть так:

Эта линия может быть использована для прогнозирования цен на новые дома. Мы рассматриваем размер дома как «входной» параметр и прогнозируемую алгоритмом цену как «выходной» параметр.

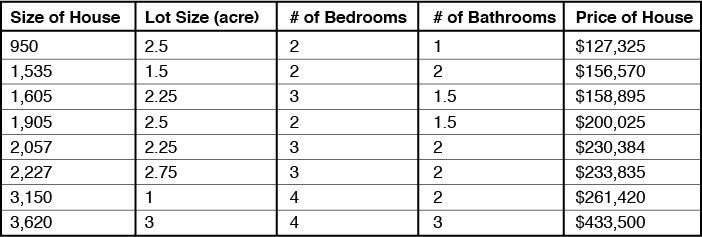
В целом, эта модель совсем упрощенная. Ведь существуют и другие значимые факторы, которые влияют на цену недвижимости — это количество комнат, количество спален, количество санузлов, общая площадь. Исходя из этого, мы можем построить более сложную модель, с таблицей данных вроде этой:

Отметим, что для этого варианта прямая не подойдёт, нам необходимо назначить каждому фактору свой вес в прогнозировании цены. Возможно, основными факторами будут размер и площадь дома, но комнаты, спальни и санузлы тоже требуют указания веса. Все эти факторы будут использоваться в качестве «входных» параметров.

Даже сейчас, нашу модель можно считать весьма упрощенной. Еще одним существенным фактором в ценах на недвижимость является локация. Цены в Сиэттле (штат Вашингтон) отличаются от цен в Галвестоне (штат Техас). Если вы попытаетесь построить подобный алгоритм в национальном масштабе, используя локацию в качестве дополнительного «входного» параметра, вы столкнетесь с серьезной задачей.

Машинное обучение можно использовать для решения всех вышеизложенных задач. В каждом из примеров мы использовали наборы данных (их чаще называют «обучающие выборки») для запуска программ, алгоритм которых основан на соответствии этим данным. Этот метод позволяет задействовать новые «входные» параметры для прогнозирования результата (в нашем случае, цены). Таким образом, способ машинного обучения, при котором система обучается на основе обучающих выборок называют «обучением с учителем».

Задачи классификации

183 см). Набор входных данных будет выглядеть приблизительно так:

На выходе данного алгоритма мы получим значение 0, если человек, вероятно, будет ниже чем 183 см и значение 1, если рост прогнозируется выше заданного. Для решения этой задачи классификации мы указываем входные параметры для специфического класса. В этом случае мы не пытаемся определить точный рост, а просто прогнозируем вероятность, что он будет выше или ниже заданного.

Примерами более сложных вопросов классификации является распознавание рукописного текста или спама в письмах.

Машинное обучение без учителя

Данный способ машинного обучения используют при отсутствии обучающей выборки. Идея заключается в том, чтобы научить систему выделять группы объектов с общими свойствами. Например, у нас может быть следующий набор данных:

Алгоритм анализирует эти данные и группирует их на основании общих свойств. В примере ниже показаны объекты «x» имеют общие свойства:

Тем не менее, алгоритм может ошибаться при распознавании объектов и группировать их примерно так:

В отличие от обучения с учителем, этот алгоритм сам определил параметры, свойственные каждой из групп и сгруппировал их. Одним из примеров реализации системы обучения без учителя является сервис Google News. Посмотрим на следующий пример:

Мы видим новость о задержании Ираном 10 американских моряков, а также ссылки на связанные новости от агентств Reuters и Bloomberg (обведено красным). Группировка этих новостей является хорошим примером системы машинного обучения без учителя, когда алгоритм учится находить связи между объектами и объединять их.

Другие примеры использования машинного обучения

Замечательным примером использования машинного обучения является алгоритм определения автора, который Moz реализовали в своем сервисе для работы с контентом. Узнать об этом алгоритме больше можно здесь. В статье по ссылке подробно описываются проблемы, с которыми специалистам из Moz пришлось столкнуться и каким образом они решили поставленную задачу.

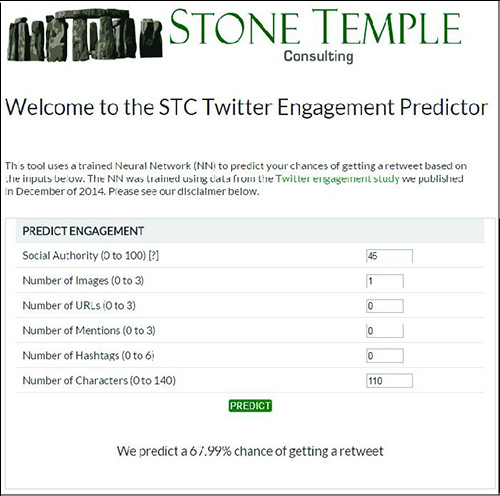
Теперь расскажу немного об упомянутом в начале статьи сервисе Twitter Engagement Predictor, система которого построена на базе нейронной сети. Пример его работы можно увидеть на скриншоте:

Программа делает бинарный прогноз ретвитнут ваш пост или нет, и в случае положительного ответа высчитывает вероятность ретвита.

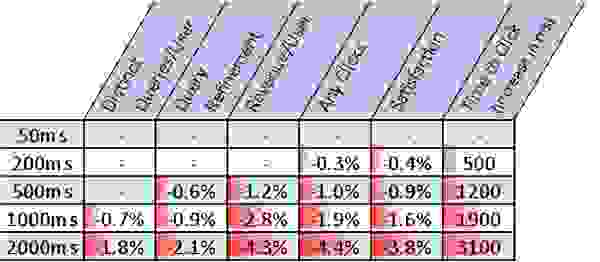
При анализе исходных данных, используемых для обучения сети можно обнаружить немало интересных нюансов, например:

Таблица показывает статистику для твитов пользователей с уровнем Social Authority от 0 до 9, без изображений, без ссылок и упоминаний, содержащих 2 хештега и от 0 до 40 символов текста. Мы видим 1156 таких твитов без ретвитов и только 17 твитов с ретвитами.

Наш алгоритм показывает, что с высокой вероятностью твит с такими параметрами не получит ретвитов, но этот прогноз будет неверным для 1,4% случаев (17 из 1173). Нейронная сеть прогнозирует вероятность получения ретвита в 2,1%.

Я рассчитал таблицу возможных случаев и обнаружил, что у нас было 102045 примеров с возможностью ошибки, или примерно 10% от всей обучающей выборки. Это значит, что нейронная сеть будет делать верные прогнозы в лучшем случае для 90% ситуаций.

Кроме того, я проверил два дополнительных набора данных (содержащие 470к и 473к примеров) через нейронную сеть, чтобы оценить точность показаний TEP. В абсолютном прогнозе (да/нет) система оказалась права в 81% случаев. Учитывая, что здесь тоже присутствовали около 10% примеров с возможной ошибкой, можно сказать, что результат довольно неплох! По этой причине сервис TEP дополнительно отображает вероятность ретвита в процентах, вместо обычного прогноза (да/нет).

Примеры алгоритмов, которые может использовать Google

Теперь, когда мы разобрались с основными способами машинного обучения, давайте перейдем ко второй части статьи и посмотрим, для чего Google может использовать эти методы:

Алгоритм Пингвин

Одним из подходов к реализации алгоритма Google Penguin может быть построение связей между ссылочными характеристиками, которые могут быть потенциальными индикаторами ссылочного спама:

Изложенный мной пример демонстрирует систему обучения с учителем, где вы тренируете алгоритм на основании имеющихся у вас данных о плохих и хороших ссылках (сайтах), обнаруженных за последние годы. После обучения алгоритма с его помощью можно проверять ссылки для определения их «качества». Основываясь на процентном соотношении «плохих» ссылок (и/или показателе PageRank), можно принимать решение – понижать рейтинг сайта в поиске или нет.

Другой подход в решении этой задачи предполагает использование базы хороших и плохих ссылок, где алгоритм сам определяет их характеристики. При таком подходе алгоритм наверняка обнаружит дополнительные факторы, которые не замечают люди.

Алгоритм Панда

После того, как мы рассмотрели потенциальные возможности алгоритма Пингвин, ситуация немного прояснилась. Теперь представим возможности алгоритма оценки качества контента.

Как машинное обучение влияет на SEO

Ключ к пониманию степени влияния машинного обучения на SEO лежит в вопросе, зачем Google (и другие поисковые системы) использует эти методы. Важно то, что существует сильная корреляция между качеством результатов органической выдачи и доходом Google от контекстной рекламы.

Еще в 2009 году Bing и Google проводили ряд экспериментов, которые показали, что появление даже небольших задержек в результатах поиска значительно влияют на удовлетворенность пользователей. В свою очередь, менее довольные пользователи меньше кликали на рекламные объявления, а поисковые системы получали меньший доход:

Объясняется все это очень просто. У Google полно конкурентов, и это касается не только поиска Bing. Борьба за аудиторию в остальных (непоисковых) сервисах также является формой конкуренции. Здесь уже подключаются Facebook, Apple/Siri и Amazon. Существует множество альтернативных источников получения и обмена информацией, и они каждый день работают над тем, чтобы стать лучше. Поэтому и Google должен.

Я уже предположил, что машинное обучение может использоваться в алгоритмах Пингвин и Панда, и это вполне может быть частью глобального алгоритма оценки «качества поиска». Скорее всего, вы увидим еще много примеров использования подобных алгоритмов в будущем.

Итак, что это значит?

Учитывая, что повышение удовлетворенности пользователя имеет решающее значение для Google, нам стоит рассматривать этот показатель в качестве основного фактора ранжирования для SEO. Вам нужно научиться измерять его и повышать показатель со временем. Рекомендую задать себе следующие вопросы:

Заключение

Машинное обучение стремительно распространяется. Препятствия для обучения базовых алгоритмов исчезают. Все основные компании на рынке в той или иной мере используют методы машинного обучения. Вот немного информации для чего машинное обучение использует Facebook, а вот как активно вербует специалистов по машинному обучению Apple. Другие компании предоставляют платформы, чтобы облегчить внедрение машинного обучения, например, Microsoft и Amazon.

Людям, занятым в области SEO и digital-маркетинга, стоит ожидать, что топовые компании будут активно развивать алгоритмы для решения своих задач. Поэтому лучше настраиваться на работу в соответствии с основными целями лидеров рынка.

В случае с SEO машинное обучение со временем будет повышать планку качества контента и опыта взаимодействия пользователей. Самое время учесть все эти факторы в своих стратегиях продвижения, чтобы успеть на борт стремительно движущегося лайнера технологий.

Источник