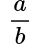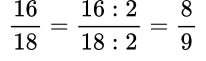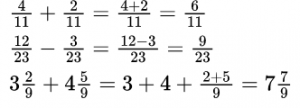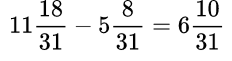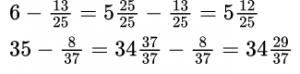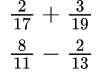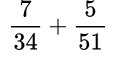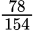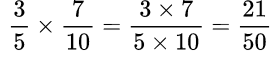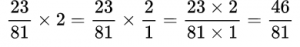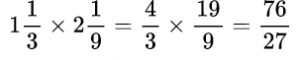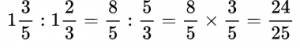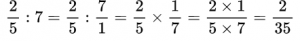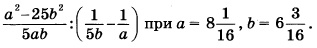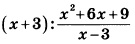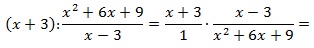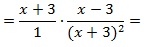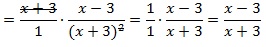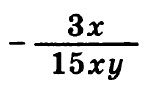примеры на обыкновенные дроби 5 класс примеры для тренировки

Задачи на дроби 5 класс

Ищем педагогов в команду «Инфоурок»

Математика – 5 класс

Задачи на нахождение дроби от числа

1. На подарок мальчику друзья собрали одну четвертую часть стоимости велосипеда. Велосипед стоил 660 рублей. Какую сумму собрали дети?

2. В школу привезли 360 учебников. Ученики 6а разгрузили 1/3 часть всех учебников. Школьники из 6б 1/4 часть от общего количества. А ученики 6в все остальные. Сколько учебников разгрузил 6в?

3. Мама купила 27 яблок. В первый день съели 1/9 часть всех яблок. Во второй день 1/6 часть оставшихся.
Сколько яблок осталось после двух дней?

4. Из 24 конфет 1/3 часть досталась сестре, а остальные мальчик поровну поделил с братом.
Сколько конфет осталось мальчику?

5. В классе 27 учеников. Четыре девятых из них девочки, а треть мальчиков носят очки. Сколько мальчиков носят очки?

6. По рецепту врача пациент должен принимать лекарство из расчета одна упаковка (21 таблетка) в неделю.
Сколько таблеток в день должен пить больной?

7. В пачке 250 листов бумаги. На перепечатывание одной рукописи ушло пачки, на перепечатывание другой рукописи остатка. Сколько осталось чистых листов?

8. Весь путь 114 км. В первый день туристы проехали всего пути. Сколько км им осталось проехать?

За первый час было расчищено от снега 5/17 всей дороги, а за второй час 9/17 всей дороги. Какая часть дороги была расчищена от снега за эти два часа? На какую часть дороги было расчищено меньше в первый час, чем во второй?

За первый день турист прошел половину всего маршрута, а за второй-2/3 его оставшейся части. Какую часть маршрута осталось пройти туристу за третий день пути?

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Математика – 5 класс

Задачи на нахождение дроби от числа

1. На подарок мальчику друзья собрали одну четвертую часть стоимости велосипеда. Велосипед стоил 660 рублей. Какую сумму собрали дети?

2. В школу привезли 360 учебников. Ученики 6а разгрузили 1/3 часть всех учебников. Школьники из 6б 1/4 часть от общего количества. А ученики 6в все остальные. Сколько учебников разгрузил 6в?

3. Мама купила 27 яблок. В первый день съели 1/9 часть всех яблок. Во второй день 1/6 часть оставшихся.
Сколько яблок осталось после двух дней?

4. Из 24 конфет 1/3 часть досталась сестре, а остальные мальчик поровну поделил с братом.
Сколько конфет осталось мальчику?

5. В классе 27 учеников. Четыре девятых из них девочки, а треть мальчиков носят очки. Сколько мальчиков носят очки?

6. По рецепту врача пациент должен принимать лекарство из расчета одна упаковка (21 таблетка) в неделю.
Сколько таблеток в день должен пить больной?

7. В пачке 250 листов бумаги. На перепечатывание одной рукописи ушло пачки, на перепечатывание другой рукописи остатка. Сколько осталось чистых листов?

8. Весь путь 114 км. В первый день туристы проехали всего пути. Сколько км им осталось проехать?

9. За первый час было расчищено от снега 5/17 всей дороги, а за второй час 9/17 всей дороги. Какая часть дороги была расчищена от снега за эти два часа? На какую часть дороги было расчищено меньше в первый час, чем во второй?

11. За первый день турист прошел половину всего маршрута, а за второй-2/3 его оставшейся части. Какую часть маршрута осталось пройти туристу за третий день пути?

Номер материала: 120675

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

На Госуслугах ввели запись детей на кружки и секции

Время чтения: 2 минуты

В школе в Пермском крае произошла стрельба

Время чтения: 1 минута

СК предложил обучать педагогов выявлять деструктивное поведение учащихся

Время чтения: 1 минута

Путин попросил привлекать родителей к капремонту школ на всех этапах

Время чтения: 1 минута

Онлайн-конференция о дизайн-мышлении в современной дошкольной педагогике

Время чтения: 2 минуты

В Тюменской области продлили на неделю дистанционный режим для школьников

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Обыкновенные дроби

теория по математике 📈 числа и вычисления

Обыкновенная дробь – это запись числа в виде:

где число a называют числителем, а число b – знаменателем дроби.

Основное свойство дроби

Если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь.

Пример №1. У первой дроби можно разделить числитель и знаменатель на одно и то же число 14, и получится равная ей дробь. Или как у второй дроби можно умножить числитель и знаменатель на одно и то же число, допустим, на 5.

Сократить дробь – значит разделить числитель и знаменатель на одно и то же число.

Пример №2. Чтобы сократить данную дробь надо вспомнить признаки делимости и увидеть, что числитель и знаменатель дроби — четные числа, значит, их можно разделить на 2, то есть дробь сокращается на 2:

Пример №3. По признаку делимости числитель и знаменатель делятся на 5, значит, сокращается данная дробь на 5.

Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями

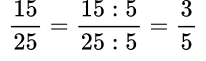
При сложении (вычитании) обыкновенных дробей с одинаковыми знаменателями нужно знаменатель оставить тем же, а числители сложить (вычесть). Если дроби смешанные, то отдельно складывают (вычитают) целые части.

Решения можно записывать короче, выполняя устно сложение или вычитание целых частей, а также – числителей.

Вычитание обыкновенной дроби из целого числа

Чтобы вычесть дробь из единицы, нужно единицу представить в виде неправильной дроби, числитель и знаменатель которой равны знаменателю вычитаемой дроби.

Пример №5. Представляем единицу в виде дроби и получаем вычитание дробей с одинаковыми знаменателями (числители можно вычесть устно).

Вычитание обыкновенной дроби из бóльшего числа

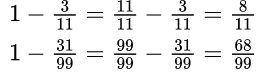
Чтобы вычесть обыкновенную дробь из числа, большего 1, необходимо представить эту дробь в виде смешанного числа, числитель и знаменатель которой равны также знаменателю вычитаемой дроби.

Сложение и вычитание дробей с разными знаменателями

Сложение и вычитание дробей с разными знаменателями требует предварительного приведения дробей к общему знаменателю. Существуют несколько приемов, которыми можно воспользоваться для нахождения общего знаменателя.

Нахождение общего знаменателя

Наименьшее общее кратное (НОК) – это наименьшее число, которое делится без остатка на данные знаменатели одновременно. Обычно его находят устно при выполнении действий с дробями.

Правило нахождения НОК рассмотрим на примере чисел 12 и 15. Пример №7. 1. Нужно разложить на простые множители каждое число:

2. Затем найти одинаковые множители (подчеркиваем):

В данном случае это только множитель 3.

3. Взять одно из данных чисел и домножить на оставшиеся (не подчеркнутые) множители другого числа:

12 домножаем на 5: 12×5=60, или

15 домножаем на 2 и 2: 15×2×2=60

Таким образом, НОК =60. Обычно достаточно просто внимательно посмотреть на числа и в уме подобрать для них НОК.

Перемножение знаменателей. Приём №2.

Нам необходимо просто перемножить знаменатели. Обычно этот прием используется тогда, когда даны простые числа (которые делятся на 1 и на само себя) и на множители их не разложить.

Пример №8.

Для нахождения общего знаменателя в первом случае: 17×19=323, во втором: перемножаем 11 и 13, получаем 143.

Последовательный подбор. Приём №3.

Данный способ можно применить для небольших чисел устно: возьмем больший из знаменателей, умножим его на 2 и проверим, делится ли это число на второй знаменатель. Если нет, то умножим последовательно на 3, 4 и проверим аналогично.

Пример №9. Возьмем число 51, умножим на 2, получим 102 — видим, что 102 делится на 34, поэтому 102 и будет общий знаменатель.

После того, как мы научились находить общий знаменатель, приступаем непосредственно к алгоритму сложения (или вычитания) обыкновенных дробей с разными знаменателями.

Находим общий знаменатель. Можно использовать прием, когда умножаем 11 и 14, так как 11 — простое число. Следовательно, общий знаменатель равен 154. Находим дополнительный множитель к каждому числителю:

Выполняем умножение в числителе: Выполняем сложение дробей с одинаковыми знаменателями:

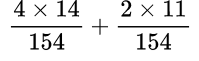
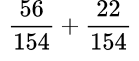
Умножение обыкновенных дробей

При умножении обыкновенных дробей получают дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.

При умножении обыкновенной дроби и целого числа необходимо целое число представить в виде дроби, числитель которой равен этому числу, а знаменатель равен 1 (что по сути означает перемножение числителя единственной первой дроби и целого числа, знаменатель же остается от первой дроби, так не меняется при умножении на единицу).

Если даны смешанные дроби, то необходимо сначала смешанную дробь перевести в неправильную, а затем выполнить умножение.

Пример №11. Здесь числитель 3 умножили на числитель 7, знаменатель 5 на знаменатель 10.

Пример №12. Случай, когда мы находим произведение дроби и целого числа. Целое число представили в виде дроби со знаменателем 1.

Пример №13. Нам даны смешанные дроби, переводим их в неправильные для выполнения умножения.

Деление обыкновенных дробей

При делении обыкновенных дробей необходимо делимое (то есть первую дробь) умножить на перевернутую вторую дробь, то есть дробь, обратную второй.

Если даны смешанные числа, то перед выполнением деления их необходимо перевести в обыкновенные неправильные дроби.

Если дробь нужно разделить на целое число, то его сначала нужно представить в виде дроби, а затем выполнить деление по правилу.

Пример №14. Делимое умножаем на число, обратное делителю. 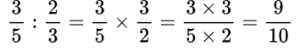Пример №15. Смешанные дроби сначала переводим в неправильные, а затем выполняем деление.

Пример №16. Деление дроби на целое число, где целое число 7 представлено в виде обыкновенной дроби.

Найдите значение выражения:

Упрощение заданного выражения нужно начать с преобразований в скобках. Здесь следует привести дроби к общему знаменателю:

теперь переходим от деления дробей к их умножению:

затем 1) сокращаем дроби на 5ab; 2) в числителе первой дроби раскладываем выражение, используя формулу сокращенного умножения для разности квадратов:

сокращаем выражение на (a–5b): Представим числовые значения для a и b в виде неправильных дробей (для удобства вычислений): Подставим полученные значения в выражение и найдем конечный результат: Ответ: 39

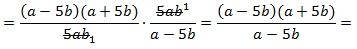
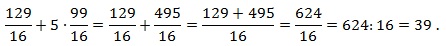
pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите значение выражения при x = 12:

Выполним тождественные преобразования выражения, чтобы упростить его. 1-й шаг – переход от деления дробей к их умножению:

далее в знаменателе второй дроби сворачиваем выражение по формуле сокращенного умножения (используем ф-лу для квадрата суммы):

теперь сокращаем выражение (в числителе первой дроби и в знаменателе второй) и приходим к окончательно упрощенному виду:

Подставляем числовое значение для х в полученное выражение и находим результат:

Ответ: 0,6

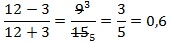
pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите значение выражения

В первую очередь в заданиях такого типа необходимо упростить выражение, а затем подставить числа. Приведем выражение к общему знаменателю — это b, для этого умножим первое слагаемое на b, после этого получим в числителе:

Приведем подобные слагаемые — это 9b² и — 9b², в числителе остается 5a. Запишем конечную дробь:

Вычислим её значение, подставив числа из условия:

pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите значение выражения:

Итак, в данном задании при вычитании дробей нам необходимо привести их к общему знаменателю. Общий знаменатель — это 15 x y, для этого необходимо первую дробь домножить на 5 y — и числитель и знаменатель, естественно:

Далее, после того как дроби приведены к общему знаменателю, можно производить вычисления. Вычислим числитель:

5 y — (3 x + 5 y) = 5 y — 3 x — 5 y = — 3 x

Тогда дробь примет вид:

Выполнив простые сокращения числителя и знаменателя на 3 и на x, получим: — 1/5 y

Подставим значение y = 0,5: — 1 / (5 • 0,5) = — 1 / 2,5 = — 0,4

pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите значение выражения:

В данном случае, в отличие от первого, мы будем упрощать выражение вынося за скобки, а не раскрывая их.

Сразу можно заметить, что b присутствует у первой дроби в числителе, а у второй — в знаменателе, поэтому можем их сократить. Семь и четырнадцать тоже сокращаются на семь:

Далее выносим из числителя второй дроби a:

Подставляем значение a = 13:

pазбирался: Даниил Романович | обсудить разбор | оценить

Какое из данных ниже чисел является значением выражения?

Заметим, что в знаменателе присутствует разность (4 — √14), от которой нам необходимо избавиться. Как же это сделать?

Для этого вспоминаем формулу сокращенного умножения, а именно разность квадратов! Чтобы правильно её применить в этом задании необходимо помнить правила обращения с дробями. В данном случае вспоминаем, что дробь не изменяется, если числитель и знаменатель домножить на одно и то же число или выражение. Для разности квадратов нам не хватает выражения (4 + √14), значит, домножим на него числитель и знаменатель.

После этого в числителе получим 4 + √14, а в знаменателе разность квадратов: 4² — (√14)². После этого знаменатель легко вычисляется:

Суммарно наши действия выглядят так:

pазбирался: Даниил Романович | обсудить разбор | оценить

Аналогично предыдущим заданиям вычисляем знаменатель: для этого приводим дроби к общему знаменателю — это 84. Для этого первую дробь умножаем на 4, а вторую на 3, получим:

1/21 + 1/28 = 4/84 + 3/84

Итак, мы получили в знаменателе 7/84, теперь делим числитель на знаменатель — это все равно что умножить 1 на обратную 7/84 дробь:

1 / ( 7 / 84 ) = 1 •84/7 = 84/7

Далее остается поделить 84 на 7:

pазбирался: Даниил Романович | обсудить разбор | оценить

Можно решать задачу напрямую — вычисляя значения последовательно, это не должно составить труда, однако решение будет долгим и с большими вычислениями. Здесь можно заметить, что 1/3 присутствует как в уменьшаемом — 6 • (1/3)², так и в вычитаемом — 17 • 1/3, поэтому её можно легко вынести за скобку.

Проведя вычисления в скобках, получим:

pазбирался: Даниил Романович | обсудить разбор | оценить

Источник

Тренажер «Дроби» онлайн

Данный тренажер является третьим в линейке тренажеров по математике для развития навыков устного счета с удобным, интуитивно-понятным интерфейсом.

Онлайн тренажер «Дроби»

Работа тренажера также основана на генерации примеров по математике с различными видами дробей, изучаемых в средних классах школы. Решение примеров способствует развитию скорости и качества устного счёта.

Приложение благоприятно влияет на умственную деятельность как детей, так и взрослых.

Режимы счёта

На странице настроек режима можно задавать необходимые параметры генерации примеров с дробями для любого класса.

Онлайн тренажер «Дроби» позволяет генерировать примеры с любыми видами дробей, с любым из четырёх арифметических действий.

В приложении отсутствуют режимы «Уравнение» и «Сравнение» из-за их избыточной сложности. Работа проходит только в режиме «Пример» с возможным использованием следующих типов дробей:

Также имеется возможность включить обязательную проверку ответа на сокращение дробной части числа и выделение целой части числа (если имеется). Понять, нужно ли сокращать ответ можно по красному индикатору * на странице настроек и странице ввода ответа.

Все изменения настроек сразу применяются и Вы тут же можете увидеть как будет выглядеть новый пример в графе «Например». Когда подбор нужных характеристик окончен, нажмите на кнопку ПОЕХАЛИ.

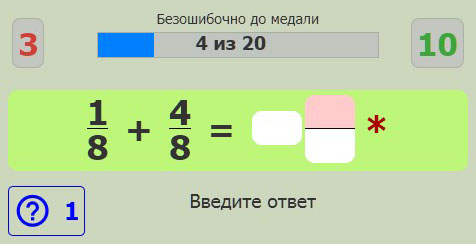
Процесс счёта

Вверху представлены 4 кнопки быстрого доступа: к главной странице сайта, профилю пользователя. Также есть возможность включить/отключить звуковые уведомления или перейти к Подробному решению текущего примера.

Вы решаете заданый пример, вводите ответ по частям (целое, числитель, знаменатель) в соответствующие поля с помощью экранной клавиатуры, нажимаете на кнопку ПРОВЕРИТЬ. Если затрудняетесь дать ответ, воспользуйтесь подсказкой. После проверки ответа Вы увидите сообщение либо о правильно введенном ответе, либо об ошибке.

Количество правильных, неправильных ответов и число подсказок можно увидеть в соответствующих индикаторах.

Прогресс и достижения

Для получения медали, в зависимости от степени её «классности» (бронзовая, серебряная или золотая), необходимо безошибочно решить 20, 50 и 100 примеров соответственно. Медаль высшей категории заменяет собой предыдущую, и выдается единоразово. На полоске прогресса наглядно видно сколько примеров осталось решить для достижения цели. При получении медали прогресс не сбрасывается, таким образом чтобы получить, например, серебряную медаль достаточно решить еще 30 примеров безошибочно.

Узнать, получили ли Вы уже медаль за конкретный режим можно на странице «Статистика» в профиле или в самом приложении.

Такой интерфейс делает процесс решения математических примеров более интересным, являясь также простой мотивацией для детей.

Подробное решение примеров

В любой момент работы с тренажером вы можете перейти в разделу «Подробного решения примера», если обычной подсказки в виде верного ответа вам не достаточно. Для этого кликните на соответствующую иконку сверху, либо перелестнув страницу вниз.

Здесь вы сможете посмотреть подробное решение примера с дробями со всеми преобразованиями, сокращениями и упрощениями.

Дополнительная информация

Хотим также обратить внимание, что ссылка на какой-либо режим имеет довольно простой вид:

домен сайта + раздел приложения + кодировка данного режима

например: matematika.club/drobi/#60101

Таким образом Вы легко можете пригласить любого человека посоревноваться в решении арифметических примеров по математике, просто передав ему ссылку на текущий режим.

Источник