применение законов кирхгофа на практике
БИЛЕТ 13?— Законы Кирхгофа, их практическое применение.
Применение законов Кирхгофа Законы Кирхгофа широко применяются в различных видах цепей, которые могут быть последовательными либо параллельными. Наиболее типичным примером последовательной цепи служит елочная гирлянда, где все лампочки соединяются в последовательную цепь. В такой цепи в соответствии с законом Ома напряжение постепенно падает. В параллельных цепях напряжение остается одинаковым, а сила тока каждого элемента напрямую зависит от его сопротивления. Определение токов, проходящих по каждому узлу таких цепей, производится в соответствии с первым законом Кирхгофа.
Второй закон Кирхгофа. При сложной и разветвленной цепи, она мысленно разбивается на несколько обыкновенных замкнутых контуров. Распределение тока по этим контурам происходит различными путями. В этом случае, достаточно сложно определить маршрут протекания того или иного тока. В каждом контуре у электронов происходит либо приобретение дополнительной энергии, либо ее потеря из-за возникшего сопротивления. Таким образом, общая энергия электронов в каждом замкнутом контуре имеет нулевое значение. В противном случае, с физической точки зрения, происходило бы постоянное возрастание или убывание электрического тока.
Источник: https://electric-220.ru/news/zakon_kirkhgofa/2014-01-06-483
Говоря проще сложно посчитать значения силы тока/напряжения разветвлённой цепи нервов не хватит с источниками ЭДС>1 без использования законов Киргофа.
Пример 1.2.
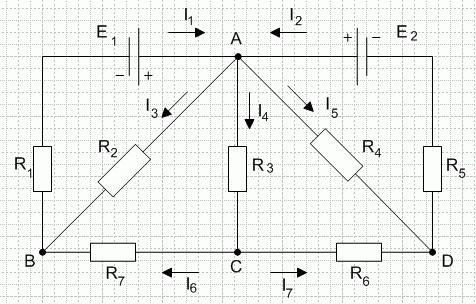
Пользуясь законами Кирхгофа, написать два выражения для тока I0 в ветви с гальванометром (рис. 1.15), приняв известным в одном случае ток I, а в другом напряжение U.
Решение.

На основании законов Кирхгофа напишем для заданной схемы с шестью неизвестными токами уравнения:
Решив совместно эти уравнения, получим выражения для тока I0 при заданном напряжении U
и при заданном токе I
Для полной характеристики электрического состояния цепи надо знать не только токи и напряжения, но также мощности источников и приемников энергии.
В соответствии с законом сохранения энергии развиваемая всеми источниками мощность равна суммарной мощности приемников и мощности потерь в источниках (из-за внутренних сопротивлений)
В левой части (1.25) суммы алгебраические. Это значит, что если при заданных направлениях действия источника ЭДС (см. рис. 1.7) или тока (см. рис. 1.8) для тока I в источнике ЭДС или напряжения U12 на выводах источника тока получится отрицательное численное значение, то этот источник в действительности не разовьет мощность, а получит ее от других источников. Соответствующее слагаемое в левой части (1.25) получится со знаком минус. Если требуется найти необходимую мощность источников питания цепи, то такие слагаемые следует записать с обратным знаком в правой части (1.25).
Закон Кирхгофа
Немецкий ученый Густав Кирхгоф наряду с другими исследованиями сформулировал основной закон, помогающий рассчитывать токи и напряжения в различных видах электрических цепей, который известен, как закон Кирхгофа.
История создания закона Кирхгофа
В середине 19-го века свойства различных электрических цепей активно исследовались с целью их дальнейшего применения на практике. К тому времени уже был совершен переход от простых цепей к более сложным и одним законом Ома было уже не обойтись. Возникла необходимость в расчетах очень сложных и разветвленных цепей.
Именно Кирхгоф сформулировал основные правила, с помощью которых стало возможным рассчитывать цепи практически любой сложности.
Первый закон Кирхгофа
В первом законе рассматривается узел цепи, представляющий собой точку схождения или разветвления трех проводов и более. В этом случае количество поступающего и исходящего электрического тока в общей сумме каждого вида будет одинаково. Таким образом, соблюдается закон сохранения электрического заряда.
Например, при Т-образном узле сумма токов, поступающих по двум проводам, равна току, выходящему по третьему проводу. В противном случае, в узле постоянно происходило бы накопление электрических зарядов, чего, практически, никогда не случается.
Второй закон Кирхгофа
При сложной и разветвленной цепи, она мысленно разбивается на несколько обыкновенных замкнутых контуров. Распределение тока по этим контурам происходит различными путями. В этом случае, достаточно сложно определить маршрут протекания того или иного тока. В каждом контуре у электронов происходит либо приобретение дополнительной энергии, либо ее потеря из-за возникшего сопротивления. Таким образом, общая энергия электронов в каждом замкнутом контуре имеет нулевое значение. В противном случае, с физической точки зрения, происходило бы постоянное возрастание или убывание электрического тока.
Применение законов Кирхгофа
Законы Кирхгофа широко применяются в различных видах цепей, которые могут быть последовательными либо параллельными. Наиболее типичным примером последовательной цепи служит елочная гирлянда, где все лампочки соединяются в последовательную цепь. В такой цепи в соответствии с законом Ома напряжение постепенно падает. В параллельных цепях напряжение остается одинаковым, а сила тока каждого элемента напрямую зависит от его сопротивления. Определение токов, проходящих по каждому узлу таких цепей, производится в соответствии с первым законом Кирхгофа.
Применение законов кирхгофа на практике

Закон Ома
Ток, напряжение и сопротивление связаны напрямую с законом Ома, описывающим отношение напряжения (приложенного к элементу) к заданному сопротивлению, в результате которого протекает ток.
| Помните, что мы всегда обозначаем эти значения следующим образом: U — напряжение, R — сопротивление, I — ток. |
Вы очень часто придется встречаться с этим законом в области электроники. К счастью, вам не нужно учить этот закон наизусть, т.к. в простейшей форме оно выражается тремя простыми формулами, которые для удобства использования обычно записываются в виде треугольника, как на картинке ниже:
| На самом деле это один паттерн (шаблон), трансформируется по мере необходимости. Достаточно запомнить одну из формул (например, U = I * R), чтобы в любой момент преобразовать ее в другую. |
Интерпретация закона Ома
Что касается тока, то закон Ома говорит, что он прямо пропорционален напряжению. Например, если мы увеличим напряжение в 10 раз, ток также возрастет в 10 раз. Это видно из формулы I = U / R (чем выше будет напряжение, тем выше будет ток).
Если сравнить с водой, то на картинке хорошо видно: при повышении уровня воды (повышается напряжение) из плотины вытекает больше воды (увеличивается ток).
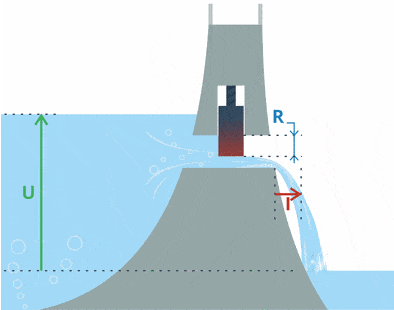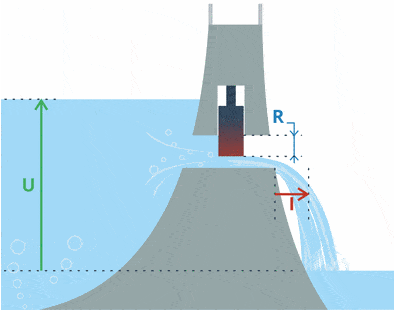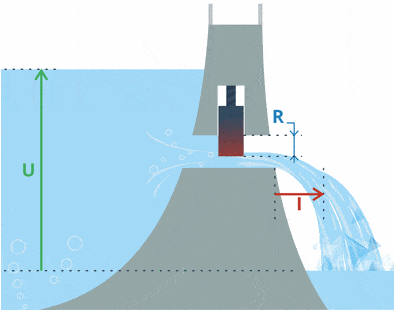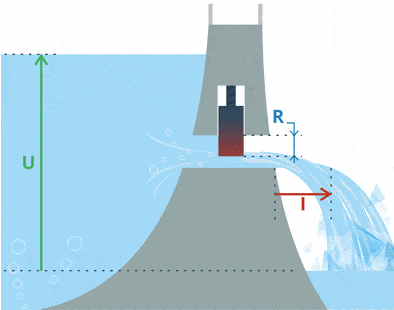
Как видите, есть возрастающее напряжение (уровень воды) с постоянным сопротивлением (положение шлюза в дамбе). Вывод: увеличение напряжения приводит к протеканию большего тока при том же сопротивлении.
U здесь означает, что ток прямо пропорционален напряжению.
Рассмотрим другой пример. На этот раз уровень воды (напряжение) будет постоянным. Изменится только степень открытия шлюза в дамбе (сопротивление):

На этот раз мы можем заметить, что при постоянном напряжении, ток, протекающий через данный элемент, зависит от его сопротивления. Вывод: ток обратно пропорционален сопротивлению (чем меньше сопротивление, тем больше тока будет протекать в цепи).
1 / R здесь означает, что ток обратно пропорционален сопротивлению.
Применим на практике закон Ома
Проверим на практике, действительно ли «работает» закон Ома. Возьмем батарейку или аккумулятор напряжением около 9 вольт. Нам нужно узнать, какой ток будет протекать, если мы замкнем цепь, подключив к ней резистор 10 кОм. Кружок с надписью «mA» на схеме обозначает наш мультиметр (тестер), настроенный на измерение амперов.
Вначале проверяем теоретически. Для этого используем известные нам формулы:
I = U / R = 9 В / 10000 Ом = 0,0009 A = 0,9 мА
| Не забудьте правильно настроить мультиметр при измерении тока! |
 |  |
Первый закон Кирхгофа
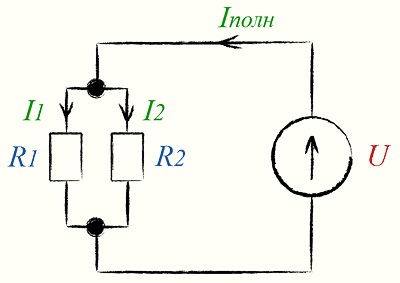
Первый закон гласит, что от узла течет столько тока, сколько и втекает в него. Узел — это место соединения проводов или компонентов в схеме.
| Это означает, что ток будет протекать одинаково через соединенные последовательно компоненты. |
Если использовать опять аналогию с водой, то можно описать такое течение так. Река, впадающая в озеро (узел № 1), разветвляется на две меньшие реки, впадающие во второе озеро (узел № 2). Таким образом мы понимаем, что одинаковое количество воды поступает в каждый узел и одинаковое количество вытекает из них.
Применим первый закон Кирхгофа на практике
Этот закон можно проверить с помощью другого эксперимента. На этот раз рассчитывать нам нечего, поэтому сразу строим схему на макетной плате. Для этого нам нужно соединить два резистора параллельно, а затем измерить ток, потребляемый каждым из них, а затем сложить полученную сумму токов вместе.
Конечно, три мультиметра нам не нужны! На схеме показаны те места, куда мы будем «подлючать» тестер.
На макетной плате такая сборка будет выглядеть следующим образом:
Затем производим соответствующие замеры мультиметром:
 |  |  |
| Измерение тока мультиметром резистора R = 10к. | Измерение тока мультиметром резистора с R = 1к. | Измерение силы тока мультиметром всей цепи. |
При сложении, общая сумма тока 0,94 + 9,08=10,12 мА. Точность до 0,1 мА. Суммируя токи, протекающие через два резистора, мы получаем ток, потребляемый батареей. Узел, в котором суммируются токи отмечен красным кружком на картинке ниже (у него 1 вход и 2 выхода):
Второй закон Кирхгофа
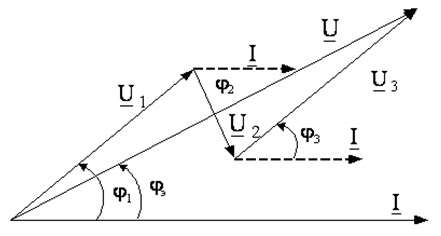
Второй закон Кирхгофа относится к напряжениям отдельных элементов цепи. В нем говорится, что если мы выберем любую замкнутую цепь, сумма напряжений от источников питания будет равна сумме напряжений на других элементах.
Это означает, что компоненты, подключенные параллельно, всегда будут иметь одинаковое напряжение, потому что они подключены к одному источнику питания. Однако для элементов, соединенных последовательно, сумма напряжений (падений напряжения) на отдельных элементах равна напряжению питания.
Этот закон можно сравнить с несколькими небольшими водопадами. Сумма высот вытекающей из них воды, должна быть равна высоте всего каскада водопадов. Это видно на картинке ниже — сумма высот, отмеченных оранжевым цветом, равна высоте, отмеченной желтым цветом:
Лучше всего закон Кирхгофа проверяется на практике. На этот раз подключите последовательно два резистора (1 кОм и 10 кОм) к батарее 9 В. Затем по очереди померяйте напряжение в трех местах:
| Чтобы измерить падение напряжения на данном элементе, один щуп вольтметра должен быть расположен перед элементом, а другой — позади него! |
Схема на макетной плате будет выглядеть так:
Самое главное — поставить щупы мультиметра в нужные места и правильно подключить батарею 9 В. Примеры измерений:
 |  |  |
| Измерение падения напряжения при R = 1k | Измерение падения напряжения при R = 10k | Измерение падения напряжения во всей цепи |
Теперь проверим результаты, суммируя измеренные напряжения: 0,86 + 8,67=9,55. Точность до 0,02 В. Такую погрешность дают: сам мультиметр и используемые компоненты.
Что такое делитель напряжения?
Делитель напряжения — не что иное, как одно из практических применений вышеуказанных законов. На практике все очень просто — последовательно соединяем два резистора и запитываем их.
Напряжение на ножках каждого из них будет пропорционально меньше, но их сумма будет равна напряжению питания. Это не что иное, как иллюстрация действия второго закона Кирхгофа. Другими словами, эта система позволяет разделить напряжение питания, благодаря чему, мы можем получить, например, 6В от батареи 9В.
Это описывается следующей формулой:
Uвход — это напряжение, питающее наш делитель. В числитель ставится номинал резистора, на котором мы хотим узнать падение напряжения. Знаменатель — это сумма обоих сопротивлений. Такое подключение мы уже производили, поэтому повторяться сейчас не будем — самое главное запомнить формулу, которая позволяет рассчитать напряжение, которое должно появиться на резисторе.
Например, посчитаем значение напряжения, которое мы получаем на делителе, состоящем из резисторов 1 кОм и 220 Ом, питаемый от 3 В. Схема будет выглядеть так:
В этом случае расчет напряжения Uвыход будет выглядеть так:
Теперь сделайте свои собственные расчеты для делителя напряжения, состоящего из резисторов 1 кОм и 330 Ом, питаемых батарекой 9 В. Рассчитайте Uвыход на резисторе 1 кОм. Соберите такую схему самостоятельно на макетной плате и измерьте напряжение. В случае проблем вернитесь к примеру выше.
Зачем нужен делитель напряжения?
В мире электроники популярны датчики, с помощью которых, измеряемые физические значения, считываются путем измерения сопротивления датчика, например, сопротивление аналогового датчика температуры зависит от температуры окружающей среды.
Микроконтроллеры (например, используемые в Arduino) не могут измерять изменения сопротивления. Однако они отлично умеют измерять напряжение.
На сегодняшний день такие делители напряжения в электросхемах не используются. Вы конечно можете использовать такой делитель для питания системы, которая требует 5 В от батареи 9 В. Но вы не должны использовать их для питания, например, средних моторов (хотя это иногда и кажется хорошей идеей), ведь от делителей напряжения невозможно получить большую силу тока! Для питания таких схем с моторами лучше использовать стабилизаторы напряжения, о которых будет рассказано в других статьях.
Что такое потенциометры?
Потенциометры представляют собой резисторы с регулируемым значением сопротивления. Поворачивая ручку потенциометра, мы влияем на его сопротивление, измеряемое между средним и крайним выводом. Примеры потенциометров:
Потенциометры на схемах представлены двумя способами (символ не имеет отношения к типу элемента):
В зависимости от исполнения корпуса, выводы или ножки могут быть расположены по-разному, но всегда легко выделить средний вывод, который является наиболее важным:
Потенциометры — это очень умные делители напряжения: ротор, из хорошо проводящего материала, движется по резестивному веществу с постоянным сопротивлением, разделяя его на два резистора. Поэтому схема потенциометра выглядит так:
Сумма сопротивлений двух резисторов, полученная таким образом, является постоянной, но величина резистора, на который подается напряжение, изменяется. Сопротивление между крайними выводами постоянно, средний вывод нашего резистора — переменное сопротивление.
Для облегчения понимания показан современный потенциометр в разборе:
Кроме того, потенциометр можно использовать как резистор с регулируемым сопротивлением — достаточно использовать один из крайних выводов и ручку. Теперь проверим теорию на практике.
Потенциометр — проверяем на практике
Вставьте потенциометр в макетную плату и измерьте сопротивление между центральным выводом и любым другим выводом. После поворота белой ручки (головки) потенциометра сопротивление должно измениться.
 |  |
| Измерения сопротивления потенциометра до поворота ручки. | Измерения сопротивления потенциометра после поворота ручки. |
Теперь проверим, как потенциометр работает, т.е. делит напряжение. Подключите питание аккумулятора к крайним контактам (ножкам) элемента (полярность не имеет значения), а затем измерьте напряжение между средним контактом и любым крайним контактом. Не забудьте правильно настроить мультиметр. Через некоторое время поворачиваем белую головку (ручку) потенциометра и делаем второе измерение. Полученные результаты могут выглядеть так:
 |  |
| Измерение напряжения на потенциометре. | Повторное измерение напряжения. |
Что такое внутреннее сопротивление?
Внутреннее сопротивление — это параметр, который является общим для каждого источника питания, но о нем часто забывают. Любой реальный источник напряжения можно в простейшем случае смоделировать, как последовательную комбинацию идеального источника и определенного сопротивления.
| Проще всего представить, батарейку или аккумулятор, внутри которого, есть резистор. |
Такое сопротивление никому не нужно, но с этим ничего не поделать; производители могут только стараться поддерживать это сопротивление на минимально возможном уровне. Это связано с составом контактных сопротивлений, крышек батарей, выводов и т.д. Кроме того, сопротивление может зависеть от температуры, сроков эксплуатации элементов и других факторов.
Это сопротивление нельзя точно самим рассчитать и не пытайтесь измерить его мультиметром! Такую информацию может предоставить только производитель батареи. К счастью, это для нас сейчас не важно, самое главное — просто знать о существовании внутреннего сопротивления.
Наличие внутреннего сопротивления иллюстрирует очень простой опыт. Давайте измерим напряжение в цепи, при течении тока через резисторы 1 кОм и 10 кОм и без них. Вот очень простая схема измерения:
 |  |  |
| Резистор 1k подключен | Резистор 10 кОм подключен | Без резистора |
Как вы можете видеть в приведенном выше примере, увеличивая ток от батареи, мы получаем более низкое напряжение. Это можно прекрасно объяснить так: чем меньше R1 (который представляет собой нагрузку) по сравнению с R2 (которое представляет собой внутреннее сопротивление), тем большее напряжение подается на R2. Для многих измерение без резистора может вызывать недоумение, потому что они думают, что это означает отсутствие сопротивления — это неправильное мышление.
| Отсутствие резистора следует понимать как бесконечно большое сопротивление. Так как, в цепи не протекает ток и батарея никак не нагружается, поэтому измеренное напряжение является самым высоким. |
Помните, что при зарядке аккумулятора слишком большим током (через резистор с низким сопротивлением), аккумулятор может нагреться и выйти из строя (может произойти утечка электролита)! При потреблении большого тока, используйте источник с достаточно низким внутренним сопротивлением и достаточно большой мощностью.
| Вышеупомянутый феномен беспокоит многих новичков, пытающихся запитать свои проекты небольшими батареями (например, 9 В). Они забывают, что высокое потребление тока (например, моторами) вызывает падение напряжения на батарее. Это может помешать работе всей системы. |
Как работают интегральные схемы стабилизации напряжения?
Наш эксперимент показал, что напряжение источника питания зависит от тока, потребляемого системой. Если потребляемый ток относительно высок, напряжение батареи может значительно упасть. Так как же работают интегральные схемы стабилизации питания, обеспечивающие стабильное значение напряжения независимо от нагрузки?
В случае интегральных схем стабилизации питания ситуация несколько иная: встроенная в них стабилизирующая схема постоянно сравнивает напряжение на выводах с напряжением, запрашиваемым пользователем, и «регулирует» его, если оно слишком низкое. Следовательно, внутреннее сопротивление таких источников питания может быть во много раз ниже, чем у даже больших батарей.
Вывод
Еще одна статья, касающаяся электронных компонентов, позади. Мы смогли изучить несколько эектронных компонентов, и даже успели обсудить важнейшие законы, управляющие миром электроники! Если вам нравятся наши статьи, то оставляйте свои комментарии. Ведь всю информацию, которую выкладываем на этом сайте, мы используем на своих уроках для работы детьми.