коэффициент учитывающий форму зуба

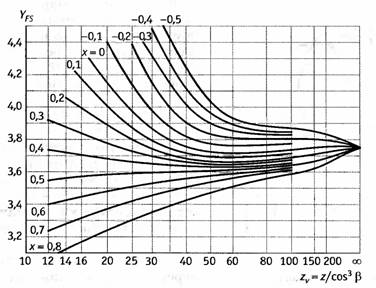
Коэффициент учитывающий форму зуба

ГОСТ 21354-87
(СТ СЭВ 5744-86)

ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР

ПЕРЕДАЧИ ЗУБЧАТЫЕ ЦИЛИНДРИЧЕСКИЕ ЭВОЛЬВЕНТНЫЕ
ВНЕШНЕГО ЗАЦЕПЛЕНИЯ

Расчет на прочность

Cylindrical evolvent gears of external engagement. Strength calculation

Дата введения 1989-01-01

1. РАЗРАБОТАН И ВНЕСЕН Министерством энергетического машиностроения СССР

Д.Э.Голлер, канд. техн. наук (руководитель темы); И.Я.Архипов, канд. техн. наук; А.Е.Мительман; В.Н.Кудрявцев, д-р техн. наук; А.А.Филипенков, канд. техн. наук; Д.Н.Решетов, д-р техн. наук; Р.М.Пратусевич, канд. техн. наук; К.И.Заблонский, д-р техн. наук; С.И.Филипович, канд. техн. наук; В.В.Брагин, д-р техн. наук; Н.М.Шоломов, канд. техн. наук; Э.В.Бабенкова, канд. техн. наук; И.Е.Тескер, канд. техн. наук

2. УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Государственного комитета СССР по стандартам от 27.10.87 N 4020

3. Срок первой проверки 1995 г., периодичность проверки 10 лет

4. Стандарт полностью соответствует СТ СЭВ 5744-86

6. ССЫЛОЧНЫЕ НОРМАТИВНО-ТЕХНИЧЕСКИЕ ДОКУМЕНТЫ

Обозначение НТД, на который дана ссылка

Номер пункта, приложения

Вводная часть, приложение 1

7. ПЕРЕИЗДАНИЕ. Октябрь 1993 г.

Настоящий стандарт распространяется на передачи зубчатые цилиндрические эвольвентные и устанавливает основные расчетные зависимости для определения контактной прочности активных поверхностей зубьев и прочности зубьев при изгибе эвольвентных цилиндрических металлических зубчатых колес внешнего зацепления передач общепромышленного применения с исходным контуром по ГОСТ 13755, модулем мм, работающих со смазкой маслом при окружных скоростях м/с.

Стандарт не распространяется на зубчатые цилиндрические эвольвентные передачи, для которых установлены особые правила расчета.

ОСНОВНЫЕ РАСЧЕТНЫЕ ЗАВИСИМОСТИ

1. РАСЧЕТ ЗУБЬЕВ НА КОНТАКТНУЮ ПРОЧНОСТЬ

При расчете определяют контактное напряжение в полюсе зацепления. При малом числе зубьев (например, ) или неблагоприятных параметрах зацепления можно дополнительно проверить контактное напряжение и в других характерных фазах зацепления.

1.1. Контактное напряжение ( ) в полосе зацепления

, (1)

; (2)

; (3)

— коэффициент, учитывающий механические свойства материалов сопряженных зубчатых колес;

— коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления (влияние радиусов кривизны боковых поверхностей и переход от окружной силы на делительном цилиндре на нормальную на начальном цилиндре);

— коэффициент, учитывающий суммарную длину контактных линий;

— коэффициент, учитывающий наклон зуба (влияние угла наклона, не охваченное другими коэффициентами);

— окружная сила на делительном цилиндре в торцовом сечении;

— рабочая ширина венца зубчатой передачи;

— делительный диаметр шестерни;

— коэффициент, учитывающий внешнюю динамическую нагрузку (не учтенную в циклограмме нагружения);

— коэффициент, учитывающий внутреннюю динамическую нагрузку;

— коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий;

— коэффициент, учитывающий распределение нагрузки между зу

1.2. Допускаемое контактное напряжение ( ), не вызывающее опасной контактной усталости материала

, (4)

где — предел контактной выносливости поверхностей зубьев, соответствующий базовому числу циклов напряжений;

— минимальный коэффициент запаса прочности;

— коэффициент, учитывающий влияние вязкости смазочного материала;

— коэффициент, учитывающий влияние исходной шероховатости сопряженных поверхностей зубьев;

— коэффициент, учитывающий влияние окружной скорости;

— коэффициент, учитывающий влияние перепада твердостей материалов сопряженных поверхностей зубьев;

— коэффициент, учитывающий размер зубчатого колес

1.3. Допускаемое предельное контактное напряжение (), не вызывающее остаточных деформаций или хрупкого разрушения поверхностного слоя

, (5)

— минимальный коэффициент запаса прочности при расчете по максимальным контактным нагрузкам.

1.4. Нагрузочная способность поверхностей зубьев. Нагрузочная способность поверхностей зубьев обеспечивается при выполнении условий любого критерия (табл.1).

Условия нагрузочной способности

,

,

,

Вероятность безотказной работы

,

Источник

Коэффициент учитывающий форму зуба

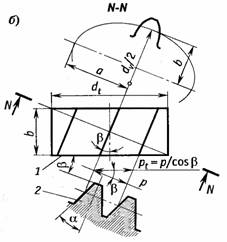
Расчетным является сечение N — N, нормальное к направ­лению зуба. В этом сечении определяют пара­метры эквивалентного колеса, которые используются при рас­чете на прочность. Профиль зуба косозубого колеса соответст­вует профилю эквивалентного прямозубого колеса с радиусом, равным радиусу кривизны эллипса по малой оси . Боль­шая полуось эллипса , малая — , радиус кривизны . Так как диаметр эквива­лентного прямозубого колеса , то эквивалентное число зубьев

,

Где z –число зубьев косозубого колеса. При расчете на прочность косозубые колеса заменяют на прямозубые с эквивалентным числом зубьев. С увеличением угла β эквивалентные параметры возрастают, что способствует повышению прочности передачи.

42. Особенно сти геометрии и условия работы косозубых цилиндрических передач. Длина линии контакта и распределение нагрузки по длине контакта.

Помимо торцевого у косозубых передач есть еще осевое перекрытие , где P_x – осевой шаг, равный расстоянию между одноименными точками двух смежных зубьев измеренному в направлении оси колеса.

Особенности геометрии определяют отличия условий работы косозубой передачи:

1) линия контакта на косозубом колесе расположены || оси вращения под углом θ к полюсной линии

2) в отличие от прямозубой в косозубой передаче зубья входят в зацепление не сразу по все длине, а постепенно. Увеличивается время контакта одной пары зубьев. Чем больше угол наклона линии зуба, тем выше плавность в зацеплении.

3) нагрузка по длине контактной линии распределяется пропорционально суммарной жесткости зубьев шестерни и колеса. При контакте одним из сопряженных зубьев в вершине жесткость меньше и нагрузка меньше.

4) в косозубой передаче в зацеплении участвуют одновременно 2-3 пары зубьев, поэтому суммарная длина контактных линий больше, чем у прямозубых.

5)Соотношение между радиусами кривизны контактирующих зубьев в косозубой передаче более благоприятно .

43. Понятие «приведенное зубчатое колесо» и приведенное число зубьев косозубых цилиндрических колес. Коэффициент, учитывающий форму зуба косозубого цилиндрического зубчатого колеса.

Расчетным является сечение N — N, нормальное к направ­лению зуба. В этом сечении определяют пара­метры эквивалентного колеса, которые используются при рас­чете на прочность. Профиль зуба косозубого колеса соответст­вует профилю эквивалентного прямозубого колеса с радиусом, равным радиусу кривизны эллипса по малой оси . Боль­шая полуось эллипса , малая — , радиус кривизны . Так как диаметр эквива­лентного прямозубого колеса , то эквивалентное число зубьев

,

Где z –число зубьев косозубого колеса. При расчете на прочность косозубые колеса заменяют на прямозубые с эквивалентным числом зубьев. С увеличением угла β эквивалентные параметры возрастают, что способствует повышению прочности передачи.

Источник

Коэффициент учитывающий форму зуба

Классификация передач. По форме различают цилиндрические, конические, реечные, эллиптические, фигурные зубчатые колеса и с неполным числом зубьев. В зависимости от взаимного расположения; зубчатых колес различают зубчатые передачи с внешним и внутренним зацеплением, а также разделяются на открытые и закрытые (рис. 81).

Преимущества. Важнейшие: компактность, высокий КПД, постоянство передаточного числа, большая долговечность и надежность в работе, возможность осуществления передачи практически любых мощностей при практически любых скоростях и передаточных отношениях, простота обслуживания. Высокая технологичность, которая обусловлена высокопроизводительным специальным оборудованием и технологиями.

Недостатки. Высокие требования к качеству изготовления и монтажа. Шум при больших скоростях. Концентрация напряжений в эвольвентных передачах при точечном контакте и чувствительность к ошибкам монтажа в передачах с линейным контактом. Поэтому для реализации преимуществ при изготовлении деталей необходимо применять высококачественные материалы и технологии изготовления.

Сферы применения. 3убчатые передачи нашли самое широкое распространение среди механических передач в машинах различных отраслей. Назначение и конструкции зубчатых передач разнообразны. Их применяют во многих приборах и почти во всех машинах, в том числе и самых тяжелых и мощных для передачи мощностей до 65 тыс.кВТ (65МВт), с диаметром колес от долей миллиметра до 6м и более. Окружная скорость зубьев может достигать 270м/с. Передаточные отношения для открытой передачи принимают 10, а для закрытой 25. КПД одной ступени зубчатой передачи при высоком качестве изготовления и монтажа может достигать 0,99.

Геометрический расчет. Передаточное отношение передачи

, (14.1)

где — число зубьев шестерни и колеса соответственно.

Номинальные значения передаточных чисел и зубчатых редукторов общего назначения, выполненных в виде самостоятельных агрегатов стандартизированы:

1-й ряд 1,00; 1,25; 1,60; 2,00; 2,50; 3,15; 4,0; 5,0; 6,3; 8,0; 10,0;12,5.

2-й рад 1,12; 1,40; 1,80; 2,24; 2,80; 3,55; 4,5; 5,6; 7,1; 9,0; 11,2.

При выборе стандартных параметров первый ряд предпочтительнее второго, а принятые значения передаточных чисел не должны отличаться от расчетных не более чем на 3%.

Расстояние между осями зубчатых колес цилиндрической передачи по межосевой линии называется межосевым расстоянием:

, (14.2)

Стандартизированы номинальные значения межосевых расстояний aw, мм:

1-й ряд 40; 50; 63; 80100; 125; 160; 200; 250; 315; 400; 500; 630; 800

Межосевое расстояние цилиндрической зубчатой передачи, равное полусумме делительных диаметров колеса d2 и шестерни при внешнем зацеплении или полуразности при внутреннем зацеплении, называется делительным межосевым расстоянием:

. (14.3)

Делительные диаметры для зубчатых колес прямозубой передачи

для косозубой и шевронной

. (14.5)

1-й ряд 1,0; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25;

2-й ряд 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14; 18; 22; 28.

Ширина венца цилиндрического зубчатого колеса определяется по одной из формул

, (14.6)

, (14.7)

где — коэффициент ширины зубчатого венца по межосевому расстоянию, а — коэффициент ширины зубчатого венца по диаметру шестерни.

Коэффициенты и связаны зависимостью:

. (14.8)

Значения коэффициентов ширины венца зубчатых колес по межосевому расстоянию выбираются из стандартного ряда: 0,1; 0,125; 0,16; 0,2; 0,250; 0,315; 0,400; 0,500; 0,630; 0,800; 1,000; 1,25 и т. д.

Рис. 82. Обозначения элементов зубчатого зацепления.

Для заданного числа зубьев и , коэффициентов смещения исходного контура и , угла наклона зубьев основные параметры эвольвентных цилиндрических колес внешнего зацепления, показанные на рис 82 в соответствии с ГОСТ 13755-81 определяются по расчетным формулам:

Параметр

Шестерня

Колесо

Диаметр вершин зубьев

Диаметр впадин зубьев

Делительный угол профиля в торцевом сечении

Коэффициент торцевого перекрытия

Рабочая ширина зубчатого венца

Коэффициент осевого перекрытия (при ширине венца )

Основной угол наклона

Кинематический и силовой расчет. Расчетная окружная скорость v цилиндрической передачи:

— шестерни ; (14.9)

— колеса ,

Окружная сила цилиндрической зубчатой передачи Ft

, (14.10)

где — крутящий момент на шестерне.

Сила давления между зубьями в цилиндрической прямозубой передаче

. (14.11)

Радиальная сила в цилиндрической передаче

, (14.12)

Осевая сила, действующая на колесо косозубой цилиндрической передачи

, (14.13)

Критерии работоспособности зубчатых передач. Учитывая виды повреждений критериями работоспособности зубчатых передач являются контактная и изгибная прочность зубьев. Проектный расчет закрытых передач малой и средней твердости выполняется на контактную выносливость. Расчет на изгибную прочность зубьев в этом случае выполняется как проверочный. Для зубчатых колес высокой прочности () размеры передачи определяются из расчета зубьев на изгиб, а проверочный расчет выполняется по контактным напряжениям. Для открытой передачи проектный расчет выполняется из условия предупреждения поломки зуба с учетом износа зубьев, проверочный расчет выполняется из условия обеспечения контактной прочности.

Проектные расчеты зубчатых передач.

Расчет зубьев на контактную прочность выполняют для зацепления в полюсе, так как выкрашивание зубьев начинается у полюсной линии. По зависимости для проектного расчета на контактную прочность зубьев определяется межосевое расстояние

, (14.14)

где — коэффициент для прямозубых передач Ка = 495, а для косозубых Ка= 430, — момент на зубчатом колесе передачи в , — коэффициент неравномерности распределения нагрузки по длине контактных линий в результате погрешностей в зацеплении и деформации зубьев, который определяется по рис. 84; — допускаемое контактное напряжение в МПа.

Рис.84. Коэффициенты неравномерности распределения нагрузки по длине контактных линий для расчета на контактную прочность.

Коэффициент ширины венца по межосевому расстоянию для редукторов принимают равным: для зубчатых колес из улучшенных сталей при несимметричном расположении = 0,315. 0,4; для зубчатых колес из закаленных сталей = 0,25. 0,315; при симметричном расположении зубчатых колес относительно опор = 0,4. 0,5; для передвижных зубчатых колес коробок скоростей = 0,1. 0,2. Принимаются стандартные значения .

Допускаемое контактное напряжение

, (14.15)

При известном межосевом расстоянии ориентировочное значение модуля передачи определяется по зависимости

, (14.27)

где — коэффициент для прямозубой передачи =1400, для косозубой и шевронной =850.

Значение модуля зацепления полученное по формуле (14.27) округляется до ближайшего стандартного значения. После определения значений межосевого расстояния и модуля определяются число зубьев и все геометрические параметры передачи по которым выполняется проверочные расчеты.

Проверочные расчеты зубчатых передач.

Расчет зубьев на контактную прочность выполняется по известным геометрическим параметрам передачи при выбранной степени точности изготовления зубьев колес по зависимости

— для прямозубых передач

; (14.28)

— для косозубых передач

, (14.29)

где , — коэффициент неравномерности распределения нагрузки между зубьями в зависимости от скорости и точности изготовления; — коэффициент динамической нагрузки, возникающей в зацеплении.

Таблица 14.3 Значения коэффициента динамических нагрузок

Степень точности

Твердость поверхностей зубьев

υ, м/с

Коэффициент неравномерности распределения нагрузки для прямозубых передач принят КНа = 1, а для косозубых коэффициент определяются по графикам на рис.87. Коэффициент динамической нагрузки определяют по таблице 14.3.

При действии на зубья кратковременных перегрузок выполняется проверка рабочих поверхностей зубьев на контактную прочность по максимальному контактному напряжению:

, (14.30)

Расчет зубьев на изгибную прочность выполняется по известным геометрическим параметрам передачи при выбранной степени точности изготовления зубьев колес по зависимости

, (14.31)

где — коэффициент учитывающий перекрытие зубьев; — коэффициент наклона зубьев; — коэффициент распределения нагрузки между зубьями; — коэффициент динамической нагрузки, возникающей в зацеплении при работе передачи, — коэффициент ширины венца зубчатого колеса по начальному диаметру шестерни.

При подстановке окружной силы по зависимости (14.10) формула (14.31) преобразуется к виду

.

Коэффициент, учитывающий перекрытие зубьев

.

При приближенных расчетах для для косозубых передач и прямозубых передач принимают .

Коэффициент наклона зубьев для прямозубых передач , для косозубых определяется по зависимости

, (14.32)

при .

Коэффициент неравномерности распределения нагрузки для прямозубых передач принят , а для косозубых коэффициент определяются по графикам на рис.87. Коэффициент динамической нагрузки определяют по таблице 14.4

Таблица 14.4 Значения коэффициента динамических нагрузок

Степень точности

Твердость поверхностей зубьев

Источник