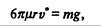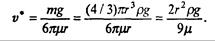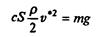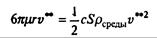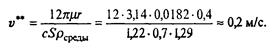Как учитывать сопротивление воздуха
аэродинамическое сопротивление воздуха
При больших скоростях движения автомобиля аэродинамическое сопротивление является преобладающим.
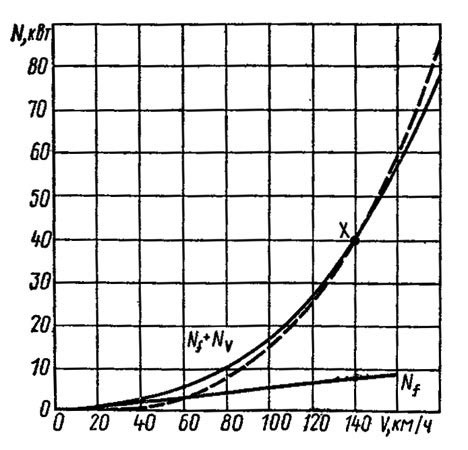
На рисунке ниже показано изменение мощностей, необходимых для преодоления сопротивления качению Nf и аэродинамического сопротивления Nv в зависимости от скорости v для автомобиля среднего класса. При скорости 60 км/ч мощности, необходимые для преодоления сопротивления качению и сопротивления воздуха, равны, что характерно для данного вида автомобилей. По сумме потребляемых мощностей можно убедиться в важности сопротивления воздуха. При скорости 80 км/ч мощность, затрачиваемая на его преодоление, в 4 раза больше, чем при скорости 40 км/ч, а при скорости выше, чем 120 км/ч, общая мощность, необходимая для движения, растет почти пропорционально кубу скорости автомобиля.
При определении мощности двигателя, необходимой для достижения максимальной скорости, большей той, которую обеспечивает номинальная мощность установленного на автомобиле двигателя, можно использовать без значительной ошибки следующее соотношение:
где N2 – требуемая мощность, кВт; N1 – достигнутая максимальная мощность, кВт; v2 – требуемая скорость, км/ч; v1 – достигнутая максимальная скорость, км/ч.
Через точку X – максимальная мощность N1 при максимальной скорости v1 – проведена кривая зависимости мощности от куба скорости. Разница между этой кривой и линией мощности, требуемой для движения при максимальной скорости, незначительна.
Показанная сумма мощностей сопротивления качению Nf и аэродинамического сопротивления Nv представляет собой мощность сопротивления равномерному движению автомобиля по горизонтальному участку дороги при безветрии.
Как зависит сила сопротивления воздуха от формы предмета и его массы
Одним из проявлений силы взаимного тяготения является сила тяжести, т.е. сила притяжения тел к Земле. Если на тело действует только сила тяжести, то оно совершает свободное падение. Следовательно, свободное падение – это падение тел в безвоздушном пространстве под действием притяжения к Земле, начинающееся из состояния покоя.
Впервые это явление изучил Галилей, но из-за отсутствия воздушных насосов он не мог провести опыт в безвоздушном пространстве, поэтому Галилей производил опыты в воздухе. Отбрасывая все второстепенные явления, встречающиеся при движении тел в воздухе, Галилей открыл законы свободного падения тел. (1590г.)
Практически воздух всегда оказывает сопротивление движению падающего тела, причем для данного тела сопротивление воздуха тем больше, чем больше скорость падения. Следовательно, по мере увеличения скорости падения сопротивление воздуха увеличивается, ускорение тела уменьшается и, когда сопротивление воздуха сделается равным силе тяжести, ускорение свободно падающего тела станет равным нулю. В дальнейшем движение тела будет равномерным движением.
Реальное движение тел в земной атмосфере происходит по баллистической траектории, существенно отличающейся от параболической из-за сопротивления воздуха. Например, если выпустить из винтовки пулю со скоростью 830 м/с под углом α = 45о к горизонту и зафиксировать с помощью кинокамеры фактическую траекторию трассирующей пули и место ее падения, то дальность полета окажется равной примерно 3,5 км. А если рассчитать по формуле, то оно окажется 68, 9 км. Разница огромная!
Сопротивление воздуха зависит от четырех факторов: 1) РАЗМЕР движущегося предмета. Большой объект, очевидно, получит большее сопротивление, чем маленький. 2) ФОРМА движущегося тела. Плоская пластина определенной площади будет оказывать гораздо большее сопротивление ветру, чем обтекаемое тело (форма капли), имеющее ту же площадь сечения для такого же ветра, реально в 25 раз большее! Круглый предмет находится где-то посередине. (Это и есть причина, по которой корпуса всех автомобилей, самолетов и парапланов имеют по возможности скругленную или каплевидную форму: она уменьшает сопротивление воздуха и позволяет двигаться быстрее при меньших усилиях на двигатель, а значит, при меньших затратах топлива). 3) ПЛОТНОСТЬ ВОЗДУХА. Нам уже известно, что один кубический метр весит около 1,3 кг на уровне моря, и, чем выше вы поднимаетесь, тем менее плотным становится воздух. Эта разница может играть некоторую практическую роль при взлете только очень с большой высоты. 4) СКОРОСТЬ. Каждый из трех рассмотренных до сих пор факторов дает пропорциональный вклад в воздушное сопротивление: если вы увеличиваете один из них вдвое, сопротивление также удваивается; если вы уменьшаете любой из них в два раза, сопротивление падает наполовину.
СОПРОТИВЛЕНИЕ ВОЗДУХА равно ПОЛОВИНЕ ПЛОТНОСТИ ВОЗДУХА, умноженной на КОЭФФИЦИЕНТ СОПРОТИВЛЕНИЯ, умноженной на ПЛОЩАДЬ СЕЧЕНИЯ и умноженной на КВАДРАТ СКОРОСТИ.
Введем следующие символы: D — сопротивление воздуха; р — плотность воздуха; А — площадь сечения; cd — коэффициент сопротивления; υ — скорость воздуха.
Теперь имеем: D = 1/2 х р х cd x A x υ 2
При падении тела в реальных условиях ускорение тела не будет равно ускорению свободного падения. В этом случае 2 закон Ньютона примет вид ma = mg – Fсопр –Fарх
А чтобы подчеркнуть, что эта сила направлена против вектора скорости.
При наличии атмосферы падающие тела помимо силы тяжести испытывают воздействие сил вязкого трения о воздух. В грубом приближении при малых скоростях силу вязкого трения можно считать пропорциональной скорости движения. В этом случае уравнение движения тела (второй закон Ньютона) имеет вид ma = mg – η υ
Масса же сферического тела постоянной плотности пропорциональна его объему, т.е. кубу радиуса m = ρ V = ρ 4/3π R3
Рассмотрим для примера падение шариков из разного материала. Возьмем два шарика одинакового диаметра, пластмассовый и железный. Примем для наглядности, что плотность железа в 10 раз больше плотности пластмассы, поэтому железный шар будет иметь массу в 10 раз больше, соответственно его инертность будет в 10 раз выше, т.е. под воздействием той же силы он будет ускоряться в 10 раз медленнее.
В вакууме на шарики действует только сила тяжести, на железный в 10 раз больше чем на пластмассовый, соответственно разгоняться они будут с одним и тем же ускорением (в 10 раз большая сила тяжести компенсирует в 10 раз большую инертность железного шарика). При одинаковом ускорении одно и то же расстояние оба шарика пройдут за одно и то же время, т.е. другими словами упадут одновременно.
В воздухе: к действию силы тяжести добавляются сила аэродинамического сопротивления и Архимедова сила. Обе эти силы направлены вверх, против действия силы тяжести, и обе зависят только от размера и скорости движения шариков ( не зависят от их массы) и при равных скоростях движения равны для обоих шариков.
T.о. результирующая трех сил действующих на железный шарик будет уже не в 10 раз превышать аналогичную результирующую деревянного, а в больше чем 10, инертность же железного шарика остается больше инертности деревянного все в те же 10 раз.. Соответственно ускорение железного шарика будет больше, чем пластмассового, и упадет он раньше.
Исследование силы сопротивления воздуха
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 63 СУГЛУБЛЁННЫМ ИЗУЧЕНИЕ ОТДЕЛЬНЫХ ПРЕДМЕТОВ»
Научное общество учащихся
Исследование силы сопротивления воздуха
Выполнил: Павлова Диана
ГЛАВА 1.Теоретические вопросы, связанные с сопротивлением
1.2.Сопротивление воздуха при движение тел……………………….….6
Глава 2. Экспериментальные методы и сложности измерения силы сопротивления…………………………………………………………….…..9
Глава 3. Экспериментальная часть………………………………..………..10
ЗАКЛЮЧЕНИЕ……………………………………………………………. 13
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ………………………. ….14
ПРИЛОЖЕНИЕ…………………………………………………………. 15
Актуальность темы. Мы настолько привыкли к тому, что окружены воздухом, что зачастую не обращаем на это внимания. Несмотря на это сила сопротивления воздуха напоминает о себе практически при любом действии, едем ли мы на автомобиле, летим ли на самолете, даже если просто кидаем камень. Нам показалось интересным изучить, что собой представляет сила сопротивления воздуха на примере таких простых случаев. Поэтому нашей основной задачей является выяснение того, от каких факторов зависит сопротивление воздуха.
Область исследования: Механика
Предмет исследования: Сопротивление воздуха
Проблема. Исходя из того что, сила сопротивления воздуха складывается из двух величин – сопротивления трения поверхности тела и сопротивления формы тела, необходимо добиваться уменьшения силы трения и уменьшения неровностей и шероховатостей на внешних деталях при изготовлении автомобилей и любых иных транспортных средств. Это приводит к уменьшению сопротивления, а значит повышается скорость автомобиля и уменьшается расход топлива при движении.
Цель моей работы ответить на вопрос, что такое сопротивление воздуха и изучить причины возникновения силы сопротивления воздуха, исследовать зависимость силы сопротивления воздуха от внешних факторов.
Задачи данной работы:
1. Изучить причины возникновения силы сопротивления воздуха.
2. Изучить методы измерения силы сопротивления воздуха.
3. Используя доступные методы, измерить сопротивление воздуха.
4. Исследовать зависимость силы сопротивления от формы, массы и скорости тела.
5. Представить в виде таблиц и графиков результаты измерений силы сопротивления воздуха.
Методы исследования: сбор информации, анализ, обобщение, изучение теоретического материала, проведение лабораторной работы.
ГЛАВА 1.Теоретические вопросы, связанные с сопротивлением
Раздел механики сплошных сред, в котором изучаются закономерности движения воздуха и других газов, а также характеристики тел, движущихся в воздухе. К аэродинамическим характеристикам тел относятся подъемная сила и сила сопротивления и их распределения по поверхности, а также тепловые потоки к поверхности тела, вызванные его движением в воздухе. В аэродинамике рассматриваются такие тела, как самолеты, ракеты, воздушно-космические летательные аппараты и автомобили.
В аэродинамике принимаются во внимание такие свойства воздуха, как плотность, давление, температура и молекулярный состав.
- Давление представляет собой силу, действующую на единицу площади. Плотность определяется как масса воздуха, содержащегося в единице объема. Температура воздуха (или какого-либо другого газа) служит мерой средней кинетической энергии молекул (равной половине произведения массы на квадрат скорости), отнесенной к единице массы.
Важной физической характеристикой газа, зависящей только от температуры, является скорость звука. Скорость звука a (м/с) в воздухе можно вычислить, зная абсолютную температуру T (K), по формуле.
Связь между давлением p, плотностью r и абсолютной температурой T дается формулой p = rRT, где R – газовая постоянная величина. Изменение плотности прямо пропорционально изменению давления.
1.2 Сопротивление воздухапри движение тел
Что такое сила сопротивления воздуха? Речь здесь идет, прежде всего, о прикладных технических задачах, при решении которых на первых порах забывается, что существует сила сопротивления воздуха. Она напоминает о себе практически при любом действии. Вы не задумывались, почему автомобили имеют такую обтекаемую форму и ровную поверхность? А ведь все на самом деле очень понятно. Сила сопротивления воздуха складывается из двух величин – из сопротивления трения поверхности тела и сопротивления формы тела. С целью уменьшения силы трения и добиваются уменьшения неровностей и шероховатостей на внешних деталях при изготовлении автомобилей и любых иных транспортных средств. Для этого их грунтуют, окрашивают, полируют и лакируют. Подобная обработка деталей приводит к тому, что сопротивление воздуха, воздействующее на автомобиль, уменьшается, повышается скорость автомобиля и уменьшается расход топлива при движении. Наличие силы сопротивления объясняется тем, что при движении автомобиля воздух сжимается и перед ним создается область местного повышенного давления, а за ним, соответственно, область разрежения. Надо отметить, что при повышенных скоростях движения машины основной вклад в сопротивление вносит форма авто. Сила сопротивления, формула расчета которой приведена ниже, определяет факторы, от которых она зависит.
Сила сопротивления = Сх*S*V2*r/2
Основной вклад вносят два компонента: квадрат скорости и форма автомобиля. Чем более обтекаемым будет автомобиль, тем меньше сопротивление воздуха.
Баллистическая траектория – это траектория, по которой движется тело, обладающее некоторой начальной скоростью, под действием силы тяготения и силы аэродинамического сопротивления воздуха.
Без учёта сопротивления воздуха баллистическая траектория, согласно первому закону Кеплера, представляет собой расположенную над поверхностью Земли часть эллипса, один из фокусов которого совпадает с гравитационным центром Земли. Поскольку большая часть траектории баллистических ракет достаточно большой дальности (более 500 км) проходит в разреженных слоях атмосферы, где сопротивление воздуха практически отсутствует, их траектории на этом участке являются эллиптическими.
Траектория (пули/снаряда) — линия не прямая, а приближающаяся к параболе, которая всё более отклоняется вниз от направления оси вращения пули в момент её вылета из ствола. Вследствие одновременного воздействия на пулю вращательного движения и сопротивления воздуха, стремящегося опрокинуть пулю головной частью назад, ось пули отклоняется от направления полёта в сторону вращения. Происходит это потому, что аэродинамический поток постоянно стремится приподнять головную часть пули. Поэтому она начинает занимать всё более выгодное с точки зрения сопротивления положение, так, чтобы ось вращения максимально совпадала с касательной к траектории. Это уводит её по направлению вращения.
На деривацию в частности, влияют следующие факторы:
ГЛАВА 2. Экспериментальные методы и сложности измерения силы сопротивления.
Полет на высотах в диапазоне высот от 30 км до 130 км, где реализуется свободномолекулярное течение, чрезвычайно трудно проанализировать теоретически. Экспериментальные исследования также осложняются тем, что вследствие низкой плотности потока требуется высокоточная измерительная аппаратура, с помощью которой можно было бы измерить малые подъемную силу и силу сопротивления, действующие на тело.
Для экспериментального исследования законов аэродинамики используется один из двух подходов: либо летательный аппарат, оборудованный соответствующей измерительной аппаратурой, совершает полет, либо неподвижное тело, оборудованное измерительными датчиками, обтекается воздушным потоком. Как отмечалось выше, в отношении явлений обтекания оба случая эквивалентны.
Практически все экспериментальные исследования аэродинамических явлений, связанных с обтеканием самолета, проводятся на маломасштабных моделях.
Выбор метода аэродинамического исследования зависит от его цели, однако наиболее простым, дешевым и надежным средством экспериментальных исследований является аэродинамическая труба. Модель выставляется в искусственно создаваемый воздушный поток таким образом, чтобы можно было измерить действующие на нее силы и моменты сил или исследовать особенности течения около модели.
Еще одним способом, используемым в некоторых специальных исследованиях, является испытание моделей в свободном полете. Модель выстреливается в длинную трубу, в которой давление может изменяться в широком диапазоне.
В этой части моей работы я хотела провести эксперименты, связанные с сопротивлением воздуха. Главные задачи моей работы были: исследовать зависимость силы сопротивления воздуха от материала и формы тела, а также установить зависимость сопротивления воздуха при движении тела.
Для первой работы я слепила из пластилина тела разной обтекаемостью с одинаковой массой. После, подобрала другие детали, но уже из другого материала.
Проведя эксперименты, с данными телами, я высчитала их среднею скорость и занесла все показатели в таблицу.
Высота, с которой я проводила эксперимент, была равна 2,5 м
Как рассчитать время свободного падения тела с учитыванием сопротивления воздуха?
С небольшой высоты не учитывается сопротивление обычно, много хлопот. В школе этого вообще нет, вроде. Только вот границу «небольшой высоты» я назвать не могу. Думаю, с 5км нужно учитывать, хотя кто знает.
Уравнение движения с учётом силы сопротивления выглядит так
Нужно решить это дифференциальное уравнение и найти скорость v. Для решения левую часть уравнения переносим в знаменатель правой, а приращение времени из знаменателя правой переносим в числитель левой. И тогда получаем
В левой части стоит обычный стандартный интеграл, он выражается либо через гиперболический арктангенс, либо через логарифм. Я решал через логарифмы. Не буду выкладывать промежуточные формулы, а сразу даю готовый результат
Ура. Смог проинтегрировать.
Интеграл от произведения скорости v на дифференциал времени dt даёт величину пройденного пути. Интегрируя, получаем
И тогда окончательный алгоритм решения будет немного иной:
1) задаёмся произвольной средней скоростью,
2) по средней скорости находим коэффициент сопротиваления,
3) последовательными приближениями находим время падения из формулы (5),
4) по формуле (4) находим конечную скорость,
5) делим конечную скорость на 2 и это будет новое значение средней скорости,
6) если новое значение средней скорости не совпадает со старым, повторяем расчёт заново на новое значение средней скорости.
СВОБОДНОЕ ПАДЕНИЕ ТЕЛА С УЧЕТОМ СОПРОТИВЛЕНИЯ СРЕДЫ
При реальных физических движениях тел в газовой или жидкостной среде трение накладывает огромный отпечаток на характер движения. Каждый понимает, что предмет, сброшенный с большой высоты (например, парашютист, прыгнувший с самолета), вовсе не движется равноускоренно, так как по мере набора скорости возрастает сила сопротивления среды. Даже эту. относительно несложную, задачу нельзя решить средствами «школьной» физики; таких задач, представляющих практический интерес, очень много. Прежде чем приступать к обсуждению соответствующих моделей, вспомним, что известно о силе сопротивления.
Оценим, при какой скорости для падающего вертикально шара сила сопротивления сравняется с силой тяжести (и движение станет равномерным).
Пусть r = 0,1 м, ρ = 0,8∙10 3 кг/м 3 (дерево). При падении в воздухе v* ≈ 960 м/с, в воде v*≈ 17 м/с, в глицерине v* ≈ 0,012 м/с.
При достижении достаточно большой скорости, когда образующиеся за обтекаемым телом вихри газа или жидкости начинают интенсивно отрываться от тела, значение с в несколько раз уменьшается; для шара оно становится приблизительно равным 0,1. Подробности можно найти в специальной литературе.
Вернемся к указанной выше оценке, исходя из квадратичнойзависимости силысопротивления от скорости.
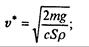
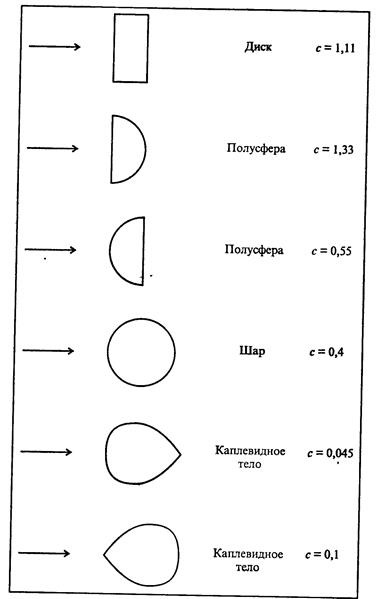
Рис. 7.6. Значения коэффициента лобового сопротивления для некоторых тел, поперечное сечение которых имеет указанную на рисунке форму (см. книгу П.А.Стрелкова)
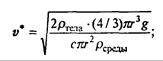
Примем r = 0,1 м, ρ = 0,8∙10 3 кг/м 3 (дерево). Тогда для движения в воздухе (ρвозд= 1,29 кг/м 3 ) получаем v* ≈ 18 м/с, в воде (ρводы ≈ 1∙10 3 кг/м 3 ) v* ≈ 0,65 м/с, в глицерине (ρглицерина = 1,26∙10 3 кг/м 3 ) v* ≈ 0,58 м/с.
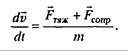
Движение является одномерным; проецируя векторное уравнение на ось, направленную вертикально вниз, получаем
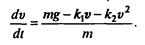
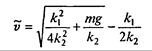
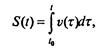
Зависимость перемещения и скорости падения «безпарашютиста» от времени (от 0 до 15 с)
| t(c) | s(m) | v (м/с) | t(с) | S(м) | v (м/с) |
| 0 | 200,1 | 35,6 | |||
| 4,8 | 9,6 | 235,9 | 36,0 | ||
| 18,7 | 17,9 | 272,1 | 36,3 | ||
| 40,1 | 24,4 | 308,5 | 36,4 | ||
| 66,9 | 28,9 | 345,0 | 36,5 | ||
| 97,4 | 31,9 | 381,5 | 36,6 | ||
| 130,3 | 33,8 | 418.1 | 36,6 | ||
| 164,7 | 35,0 | 454,7 | 36,6 |
Кроме таблицы необходимы графики зависимостей v(t) и S(t); по ним хорошо видно, как меняются со временем скорость и перемещение, т.е. приходит качественноепонимание процесса.
Приведем конкретный пример решения задачи о свободно падающем теле. Герой знаменитого фильма «Небесный тихоход» майор Булочкин, упав с высоты 6000 м в реку без парашюта, не только остался жив, но даже смог снова летать. Попробуем понять, возможно ли такое на самом деле или же подобное случается только в кино. Учитывая сказанное выше о математическом характере задачи, выберем путь численного моделирования. Итак, математическая модель выражается системой дифференциальных уравнений
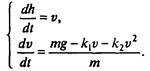
Выясним, при какой скорости сравняются линейная и квадратичная составляющие силы сопротивления. Обозначим эту скорость v**. Тогда
Ясно, что практически с самого начала скорость падения майора Булочкина гораздо больше, и поэтому линейной составляющей силы сопротивления можно пренебречь, оставив лишь квадратичную составляющую.
Отметим, что существует немало программ, моделирующих простые физические процессы типа рассматриваемого. У них реализован, в той или иной мере профессионально, диалоговый интерфейс, позволяющий вводить параметры, получать на экране таблицы, графики, движущиеся изображения. Однако в них, как правило, остаются скрытыми физические законы, определяющие процесс, ограничения модели, возможности ее усовершенствования. Такие программы полезны скорее как сугубо иллюстративные.
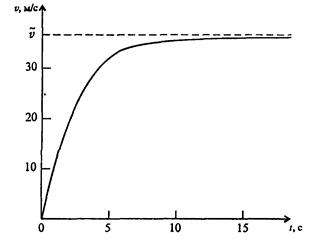
Вычисления производились до тех пор, пока «безпарашютист» не опустилсянаводу. Примерно через 15 с после начала полета скорость стала постоянной и оставалась такой до приземления (рис. 7.7). Отметим, что в рассматриваемой ситуации сопротивление воздуха радикально меняет характер движения; при отказе от его учета график скорости, изображенный на рисунке, заменился бы касательной к нему в начале координат.
Рис. 7.7. График зависимости скорости падения «безпарашютиста» от времени
Кроме того, в ячейках D2, D4, D6 в таблице будем хранить соответственно значения шага вычислений, массы «безпарашютиста», величины mg. Это связано с тем, что все константы также удобно хранить в отдельных ячейках, чтобы в случае их изменения не пришлось переписывать расчетные формулы. Достаточно записать
Фрагмент таблицы, где представлено решение задачи о «безпарашютнсте»
| А | В |
| t | v |
| 0 | |
| =СУММ(АЗ; D2) | =B3+D2/2* ( (D6-D8*B3^2) /D4+(D6-D8*(B3+D2*(D6-D8*B3^2)/D4)^2)/D4) |
| =СУММ(А4; D2) | =B4+D2/2* ( (D6-D8*B4^2) /D4+(D6-D8* (B4+D2* (D6- D8*B4^2)/D4)^2)/D4) |
| =СУММ(А5; D2) | =B5+D2/2*( (D6-D8*B5^2)/D4+(D6-D8*(B5+D2*(D6-D8*B5^2)/D4)^2)/D4) |
| =СУМM(А6; D2) | =B6+D2/2* ( (D6-D8*B6^2) /D4+ (D6-D8* (B6+D2* (D6-D8*B6^2)/D4)^2)/D4) |
| =СУММ(А7; D2) | =B7+D2/2*((D6-D8*B7^2)/D4+(D6-D8*(B7+D2*(D6-D8*B7^2)/D4)^2)/D4) |
формулу правильно один раз, а затем скопировать в остальные ячейки, при этом, как известно, она «настраивается» на соответствующую ячейку.