измерить объем фигуры значит подсчитать сколько в ней помещается

Площадь. Площадь прямоугольника

Фигуры на рисунке 146, а и б равны, так как они совпадают при наложении.

Очевидно, что фигуры на рисунке 146, а и в не равны. Однако каждая из них состоит из семи квадратов со стороной 1 см.

Про такие фигуры говорят, что их площади равны.

С такой величиной, как площадь, вы час

то встречаетесь в повседневной жизни: площадь квартиры, площадь дачного участка, площадь поля и т.п.

Опыт подсказывает вам, что равные земельные участки имеют равные площади, что площадь квартиры равна сумме площадей всех ее помещений (комнат, кухни, прихожей и т.д.). Эти примеры иллюстрируют свойства площади фигуры.

1 ) Равные фигуры имеют равные площади.

2 ) Площадь фигуры равна сумме площадей фигур, из которых она состоит.

Как можно измерить площадь фигуры?

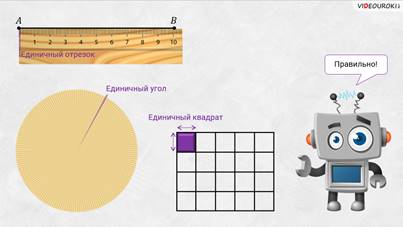
Напомним, что для измерения отрезков мы вводили единичный отрезок, а для измерения углов − единичный угол.

Вообще, когда нужно измерить какую−либо величину, вводят единицу измерения.

За единицу измерения площади выбираю квадрат, сторона которого равна единичному отрезку. Такой квадрат называют единичным.

Площадь квадрата со стороной 1 м называют квадратным метром.

Площадь квадрата со стороной 1 см называют квадратным сантиметром.

Площадь квадрата со стороной 1 мм называют квадратным миллиметром.

Измерить площадь фигуры − значит подсчитать, сколько единичных квадратов в ней помещается.

Если одна сторона прямоугольника равна 6 см, а другая сторона 4 см, то этот прямоугольник можно разделить на 4 * 6 единичных квадратов (рис. 147 ). Поэтому его площадь равна 4 * 6 = 24 (см 2 ).

Площадь прямоугольника равна произведению длин его соседних сторон:

S = ab

Поскольку у квадрата все стороны равны, то его площадь вычисляют по формуле:

S = a 2

где a − длина стороны квадрата. Именно поэтому втору степень числа называют квадратом числа.

Вы знаете, что равные фигуры имеют равные площади. Однако если площади фигур равны, то не обязательно будут равными сами фигуры (см. рис. 146 ).

Для измерения площади земельных участков используют различные единицы измерения. Например: ар, гектар.

В быту 1 ар называют соткой.

Источник

Объём прямоугольного параллелепипеда

Урок 23. Математика 5 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Объём прямоугольного параллелепипеда»

Представим себе такую историю…

– Паша, а ты когда-нибудь собирал кубик Рубика? – спросил Саша.

– Конечно! И не один раз, – ответил Паша. – Кстати, кубик Рубика отличная игрушка-головоломка, которая развивает логическое мышление.

– Да, мне тоже он очень нравится! – продолжил Саша. – Я вот сегодня собрал кубик Рубика за 15 минут. Пока собирал, задумался, а сколько всего маленьких кубиков в нём?

– И в правду, – задумался Паша, – и сколько же их там?

– Не знаю! – ответил Саша. – Сколько ни пытался их пересчитать, всё сбивался. В общем, так и не получилось у меня их сосчитать.

– А давай спросим у Электроши! – предложил Паша. – Он точно знает, как их посчитать.

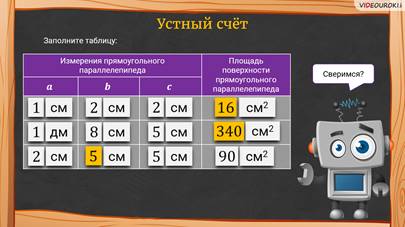
– Ребята, прежде чем я вам расскажу о прямоугольном параллелепипеде, давайте немного разомнёмся и выполним устные задания, – предложил Электроша.

– Давайте сверимся! Посмотрите, что у вас должно было получиться!

– А теперь вернёмся к вашему вопросу, – продолжил Электроша. – Только сначала ответьте мне на вопрос: какую форму имеет кубик Рубика?

– Кубик Рубика имеет форму прямоугольного параллелепипеда, а точнее – форму куба, – ответили мальчишки.

– Молодцы! – похвалил ребят Электроша. – Важным свойством любого геометрического тела является его вместимость, то есть объём фигуры. Величина объёма даёт нам представление о том, какую часть пространства занимает интересующий нас объект.

Кстати, с такой величиной, как объём, мы очень часто встречаемся в нашей жизни. Может, вы сможете привести примеры, когда мы интересуемся объёмом? – спросил у ребят Электроша.

– Например, объём коробки с соком, объём бассейна, объём школьного кабинета, – начал Саша.

– Ещё нам нужно знать объём топливного бака машины, показатели потребления газа или воды на счётчиках, – продолжил Паша.

– Хорошие примеры! – похвалил ребят Электроша. – А как вы думаете, что нужно знать для того, чтобы измерить объём? – спросил у ребят Электроша.

– Наверное, нужно знать единицу измерения объёмов, – предположили мальчишки.

– Правильно! – подтвердил Электроша. – Напомню, что для измерения отрезков мы вводили единичный отрезок, для измерения углов – единичный угол, а для измерения площадей фигур – единичный квадрат.

Для измерения объёмов также вводятся единицы измерения. За единицу измерения объёма выбирают куб, ребро которого равно единичному отрезку. Такой куб называют единичным.

Например, объём куба с ребром 1 миллиметр называют кубическим миллиметром. Пишут так: .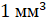

Объём куба с ребром 1 сантиметр называют кубическим сантиметром. Пишут так: .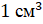

Объём куба с ребром 1 дециметр называют кубическим дециметром. Пишут так: .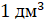

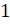
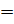
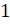
Всем хорошо известна и такая единица объёма, как 1 литр. Пишут так дм 3 л. Это другое название кубического дециметра.

Объём куба с ребром 1 метр называют кубическим метром. Пишут так: .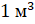

Объём куба с ребром 1 километр называют кубическим километром. Пишут так: .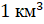

Легко заметить, что название единицы объёма получается из названия единицы длины присоединением прилагательного «кубический».

– Как вы думаете, что значит измерить объём фигуры? – спросил у ребят Электроша.

– Измерить объём фигуры – значит подсчитать, сколько единичных кубов в ней помещается, – сказали мальчишки.

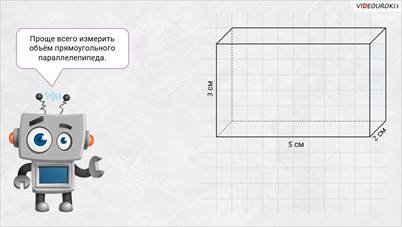
– Молодцы! – похвалил ребят Электроша. – Проще всего измерить объём прямоугольного параллелепипеда. Чем мы сейчас и займёмся.

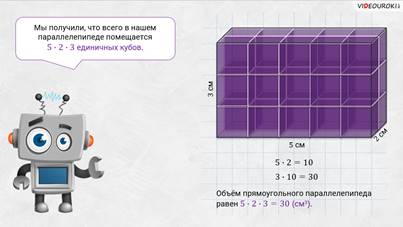
– Посмотрите: на листке бумаги изображён прямоугольный параллелепипед со следующими измерениями: длина 5 сантиметров, ширина 2 сантиметра и высота 3 сантиметра. Давайте посчитаем, сколько единичных кубов может в нём поместиться.

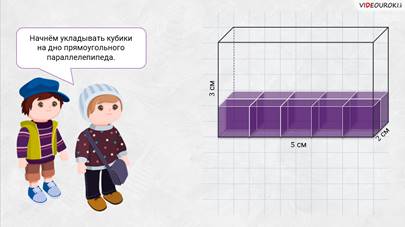
– Начнём укладывать кубики на дно прямоугольного параллелепипеда, – предложили мальчишки. – Итак, сначала положим на дно ряд единичных кубиков со стороной 1 сантиметр вдоль длинной стены. Видим: поместилось 5 таких кубиков. Затем вдоль этих кубиков уложим ещё 1 ряд. Тоже получим ещё пять кубиков.

– Хорошо! – сказал Электроша. – Тогда сколько всего кубиков у вас поместилось на дне прямоугольного параллелепипеда?

– На дне параллелепипеда помещается слой из 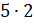единичных кубиков, то есть слой из 10 кубов.

– Молодцы! – похвалил ребят Электроша. – А чтобы заполнить весь прямоугольный параллелепипед, сколько в него нужно вложить таких слоёв?

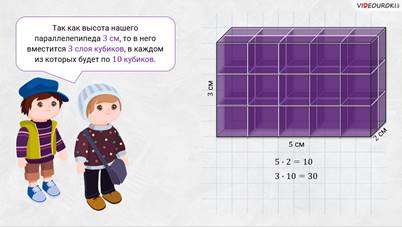
– Так как высота нашего параллелепипеда 3 сантиметра, то в него вместится 3 слоя кубиков, в каждом из которых будет по 10 кубиков. Тогда получается, что весь прямоугольный параллелепипед можно заполнить 30 кубиками.

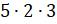
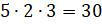
– Всё правильно! – согласился Электроша. – Мы получили, что всего в нашем параллелепипеде помещается единичных кубов. Поэтому объём нашего параллелепипеда равен (см 3 ).

– Электроша, получается, что три измерения прямоугольного параллелепипеда позволяют посчитать, сколько всего кубиков в нём поместится? – спросил Паша.

– Да, – ответил Электроша. – Запомните! Объём прямоугольного параллелепипеда равен произведению трёх его измерений.

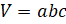
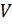
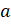
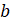
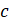
Формулу для вычисления объёма прямоугольного параллелепипеда в буквенном виде можно записать следующим образом: , где – объём, , и – измерения прямоугольного параллелепипеда. При вычислениях обязательно нужно обращать внимание, чтобы все измерения прямоугольного параллелепипеда были выражены в одинаковых единицах.

– А теперь давайте решим одну задачку, – предложил Электроша. – Определите объём блока бумаги, если длина одного листа 20 миллиметров, ширина – 15 миллиметров, а всего в блоке помещается 500 таких листов (считать толщину листа равной 1 миллиметру).

– Сначала вычислим площадь одного листа, – сказал Паша, – она будет равна 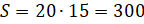(мм 2 ).

– А потом площадь этого листа умножим на количество листов, помещающихся в блоке, – продолжил Саша, – то есть 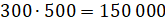(мм 3 ).

– Молодцы! – похвалил ребят Электроша. – Обратите внимание: блок бумаги имеет форму прямоугольного параллелепипеда. Значит, мы с вами сейчас нашли объём параллелепипеда, но с помощью другой формулы. Запомните! Объём прямоугольного параллелепипеда равен произведению площади основания на высоту.

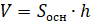
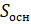
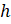
В буквенном виде эту формулу записывают так: , где – площадь основания прямоугольного параллелепипеда, – его высота.

– А теперь давайте всё же вернёмся к вашему первоначальному вопросу, – продолжил Электроша. – Вы хотели выяснить, сколько кубиков содержится в кубике Рубика. Мы с вами уже определили, что эта замечательная игрушка имеет форму прямоугольного параллелепипеда, а если быть точнее, то форму куба. Может, вы уже сможете посчитать количество маленьких кубиков, из которых состоит кубик Рубика?

– Так, – начал рассуждать Саша, – длина нашего кубика Рубика состоит из 3 маленьких кубиков, точно такие же ширина и высота. Значит, в нашем кубике Рубика помещается 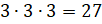маленьких кубиков.

– Всё правильно! – сказал Электроша. – Изначально кубик Рубика состоял из 27 связных между собой разноцветных кубиков, но затем его конструкция упростилась до набора из 26 маленьких кубиков, а вместо внутреннего кубика разместился хитроумный скрепляющий механизм. Кстати, а вы знаете кем, как и когда была придумана эта замечательная игрушка? – спросил Электроша.

– Не знаем, – ответили мальчишки.

– Скажу вам только, что знаменитый кубик Рубика придумал венгерский преподаватель архитектуры Эрно Рубик в 1974 году.

А вот уже историю его создания и усовершенствования вы можете изучить на досуге.

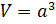
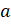
– А теперь смотрите, мы с вами определили, что наш кубик Рубика имеет форму куба. Поскольку у куба все рёбра равны, то его объём вычисляют по формуле: , где – длина ребра куба. Именно поэтому третью степень числа называют кубом числа.

А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.

Задание первое: объём класса 96 кубических метров. Найдите высоту стены, если площадь пола 32 квадратных метра.

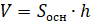
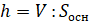
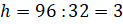
Решение: класс имеет форму прямоугольного параллелепипеда. Нам известна площадь пола, то есть площадь основания прямоугольного параллелепипеда. Значит, можем воспользоваться формулой для вычисления объёма прямоугольного параллелепипеда через площадь основания и высоту: . Выразим из этой формулы высоту: . И подставим в получившуюся формулу объём класса и площадь пола: (м). Получаем, что высота стены равна 3 метрам.

Следующее задание: длина аквариума 80 сантиметров, ширина 45 сантиметров, высота 65 сантиметров. Сколько литров воды нужно налить, чтобы уровень воды был ниже верхнего края аквариума на 5 сантиметров?

Источник

Объем параллелепипеда

Понятие объема

Чтобы без труда вычислить объём любой фигуры, нужно разобраться с определениями.

Объём — это количественная характеристика пространства, занимаемого телом или веществом.

Другими словами, это то, сколько места занимает предмет.

Объём измеряется в единицах измерения размера пространства, занимаемого телом, то есть в кубических метрах, кубических сантиметрах, кубических миллиметрах.

За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (см 3 ), кубический миллиметр (1 мм 3 ), кубический метр (1 м 3 ).

Объём всегда выражается в положительных числах. Это число показывает, какое именно количество единиц измерения есть в теле. Например, сколько воды в бассейне, сока в графине, земли в клумбе.

Два свойства объёма

Любое объемное тело имеет объем. Получается, при желании мы можем вычислить объем кружки, смартфона, вазы, кота — чего угодно.

Объем прямоугольного параллелепипеда

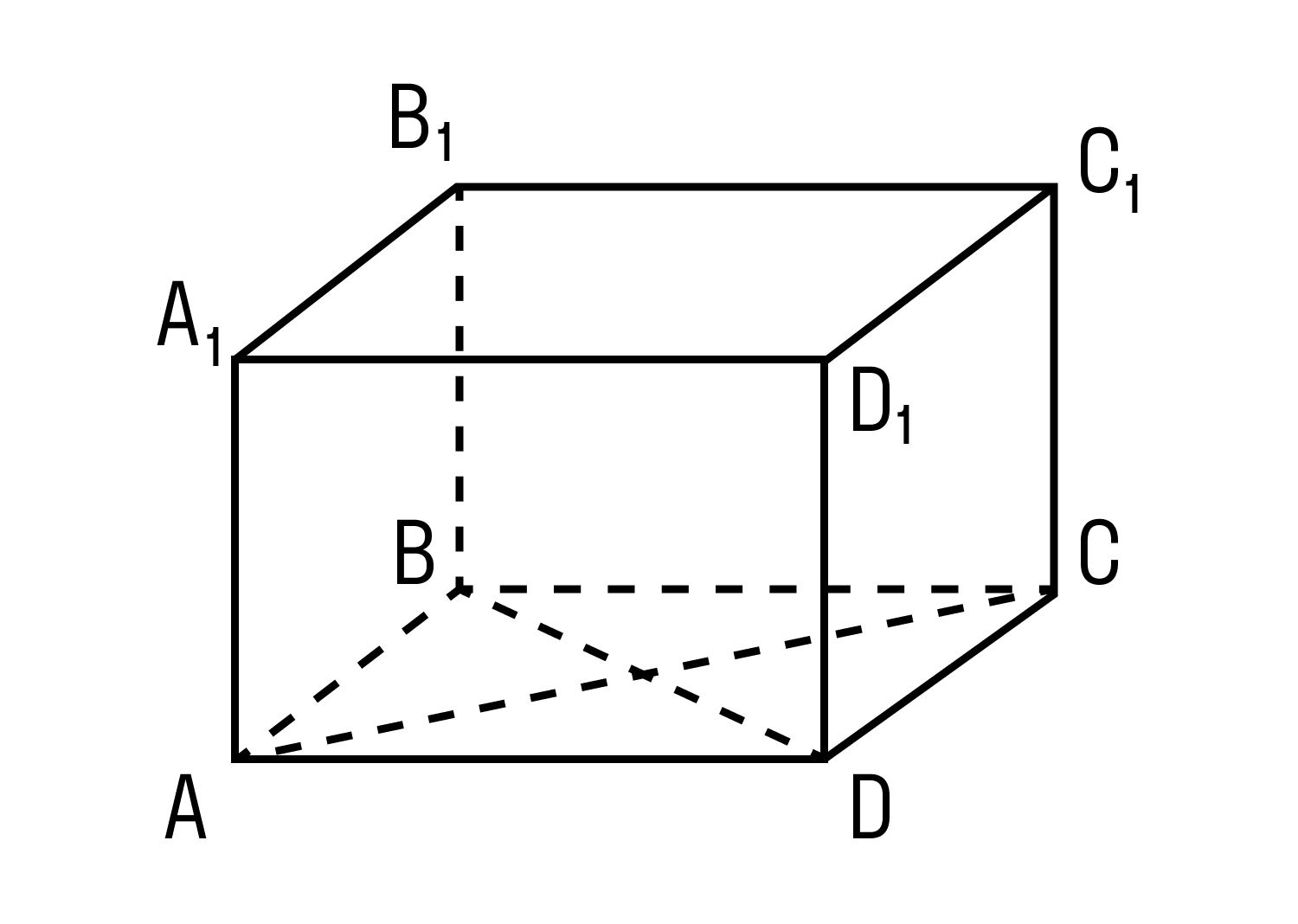
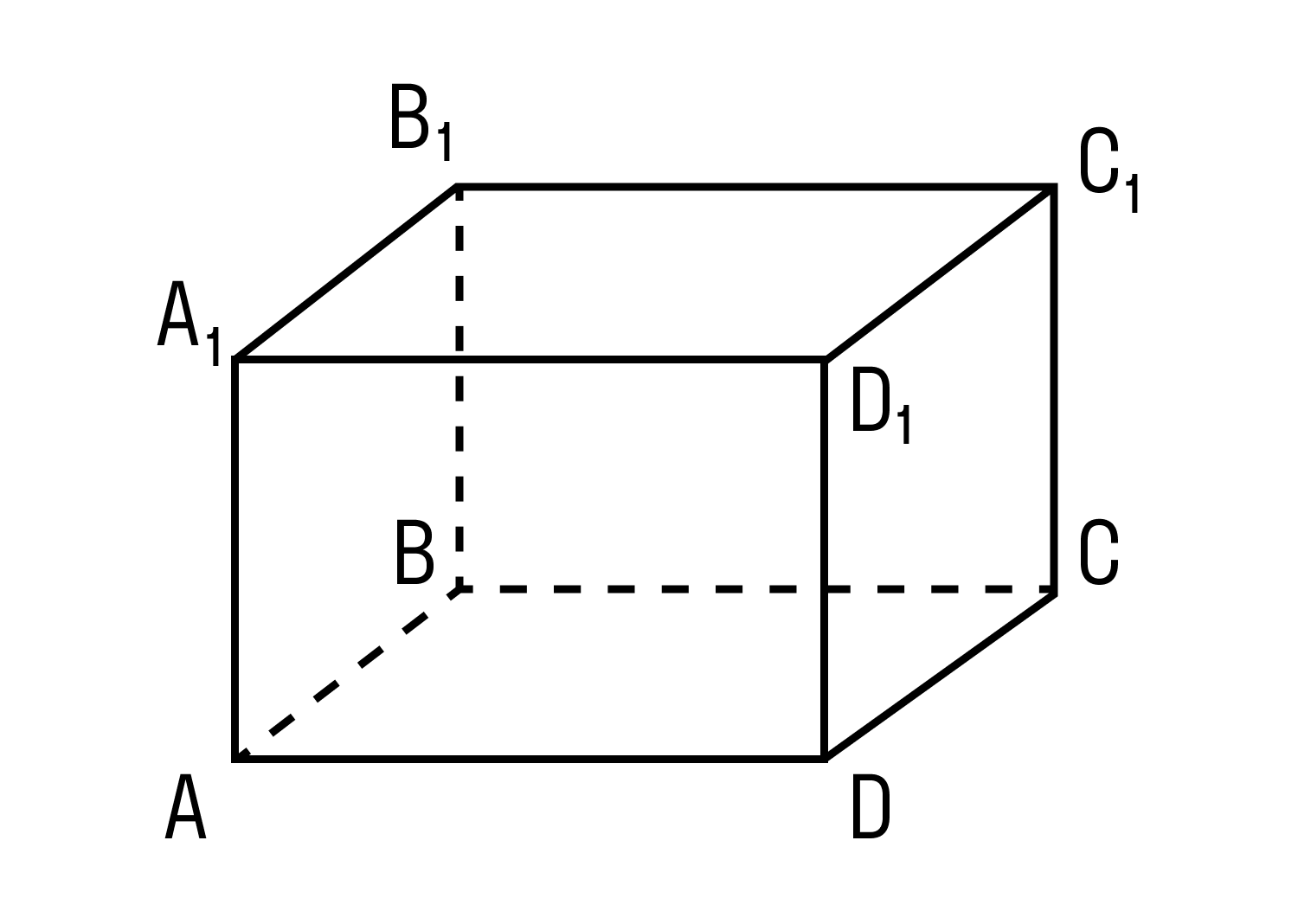
Прямоугольный параллелепипед — это многогранник с шестью гранями, каждая из которых является параллелограммом.

Прямоугольным параллелепипедом называют параллелепипед, у которого основание — прямоугольник, а боковые ребра образуют с основаниями прямые углы.

Формула объема прямоугольного параллелепипеда

Чтобы вычислить объем прямоугольного параллелепипеда, найдите произведение его длины, ширины и высоты:

V = a × b × h

Чтобы не запутаться в формулах, запоминайте табличку с условными обозначениями.

Источник

Вычисление длины, площади и объёма

Урок 12. Наглядная геометрия 5–6 классы ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Вычисление длины, площади и объёма»

Напомним, что измерить отрезок означает подсчитать, сколько единичных отрезков в нём укладывается. Измерить площадь фигуры означает подсчитать, сколько единичных квадратов в ней укладывается. Измерить объём фигуры означает подсчитать, сколько единичных кубов в ней укладывается.

Теперь сформулируем некоторые свойства произвольных фигур.

Итак, каждая плоская фигура или пространственное тело имеют форму и размеры.

Равные фигуры – это фигуры, равные по размерам и имеющие одинаковую форму.

Так, например, следующие прямоугольник и квадрат имеют равные площади (в каждом из них укладывается одинаковое число единичных квадратов), но при этом они не равны, так как имеют разные формы.

Или, например, два круга имеют одну и ту же форму, но очевидно, что их размеры не совпадают. Значит, эти два круга не равны между собой.

А вот два отрезка одинаковой длины являются равными фигурами.

Две фигуры называют равными, если они совпадают при наложении. Посмотрите, на листе бумаги изображены фигуры. Если их вырезать и совместить, то мы увидим, что они совпадают при наложении. А значит, эти фигуры равны.

Если две различные плоские фигуры можно разрезать на одинаковые части, то эти фигуры будут иметь равные площади. Такие фигуры называют равносоставленными.

Давайте возьмём прямоугольник и разрежем его на два треугольника. Сложим из полученных фигур новую фигуру – треугольник. Полученный треугольник и прямоугольник – равносоставленные фигуры, так как состоят из одного и того же набора плоских фигур.

Прямоугольник и треугольник, составленные из частей прямоугольника, имеют одинаковую площадь.

Фигуры, имеющие равные площади, называют равновеликими.

Плоские равновеликие многоугольники также являются равносоставленными.

Таким образом, можно сказать, что многоугольник всегда можно перекроить в любой другой многоугольник с такой же площадью.

Давайте следующий четырёхугольник разделим на три части. Получили два треугольника и квадрат.

Теперь переложим один треугольник вот таким образом…

В результате получим прямоугольник, площадь которого равна площади исходного четырёхугольника.

Объёмные тела, составленные из одинаковых частей, имеют одинаковый объём.

В отличие от многоугольников, два многогранника, имеющие одинаковый объём, не всегда можно разделить на одинаковые части.

Теперь возьмём прямоугольник со сторонами длиной 2 см и 3 см.

. Получается, что площадь прямоугольника увеличилась в 4 раза.

При увеличении длины каждой стороны прямоугольника в 2 раза площадь увеличилась в , то есть в 4 раза.

Таким образом, если, не меняя формы плоской фигуры, увеличить её размеры в раз, то её площадь увеличится в раз.

. Получается, что объём куба увеличился в 8 раз.

При увеличении длины ребра куба в 2 раза объём куба увеличился в , то есть в 8 раз.

Таким образом, если, не меняя формы тела, увеличить его размеры в раз, то его объём увеличится в раз.

Отметим, что площадь фигуры и объём тела не всегда удобно находить так, как мы это делали выше. Так, например, вычислить площадь участка или объём комнаты было бы удобнее с помощью некоторых формул. Ещё в начальной школе мы узнали, что площадь прямоугольника равна произведению его длины и ширины.

Если и – длины соседних сторон прямоугольника (в каких-то единицах), то его площадь равна квадратных единиц.

В буквенном виде формулу для вычисления площади прямоугольника записывают так:

– площадь, , – длины соседних сторон прямоугольника. При вычислениях важно помнить, что длина и ширина прямоугольника должны быть выражены в одних и тех же единицах измерения.

Так, площадь прямоугольника со сторонами 2 см и 3 см равна (см 2 ).

А сейчас посмотрите на следующий рисунок.

На нём изображён квадрат со стороной 4 см. Давайте вычислим его площадь. Так как квадрат – это прямоугольник, у которого все стороны равны, то воспользуемся формулой площади прямоугольника. (см 2 ).

Так как у квадрата все стороны равны, то его площадь находят по формуле:

Теперь познакомимся с формулой для вычисления объёма прямоугольного параллелепипеда.

Если , и – длина, ширина и высота прямоугольного параллелепипеда, то его объём равен кубических единиц.

В буквенном виде формулу для вычисления объёма прямоугольного параллелепипеда записывают так:

– объём, , , – измерения прямоугольного параллелепипеда. Отметим, что при вычислениях важно помнить, что длина, ширина и высота прямоугольного параллелепипеда должны быть выражены в одинаковых единицах измерения.

Куб – это прямоугольный параллелепипед, у которого все рёбра равны между собой, то его объём вычисляют по формуле:

Например, объём куба с длиной ребра 2 см равен (см 3 ).

А теперь давайте с вами решим несколько задач.

Задание первое. Выясните, являются ли квадрат со стороной 6 см и прямоугольник со сторонами 9 см и 4 см равновеликими фигурами?

Задание второе. Найдите площадь фигуры, изображённой на рисунке.

Запомните! Площадь фигуры равна сумме площадей фигур, из которых она состоит.

Задание третье. Найдите объём комнаты, если её длина равна 7 м, ширина равна 4 м, а высота стен равна 3 м.

Источник

• ← измерить матку что значит
• измерить площадь многоугольника это значит →