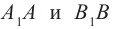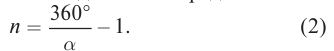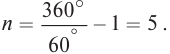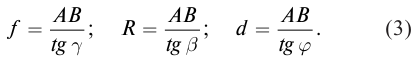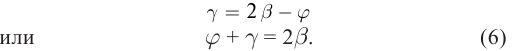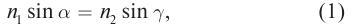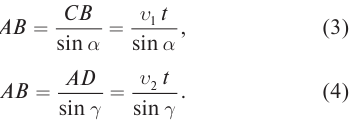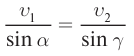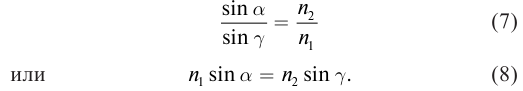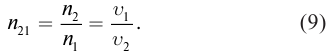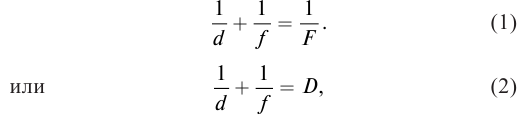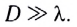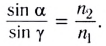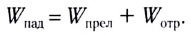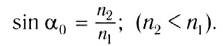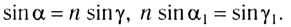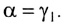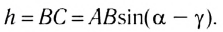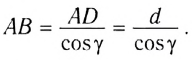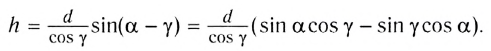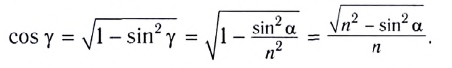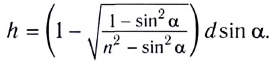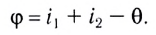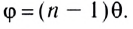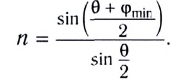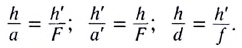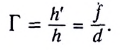Геометрическая оптика что это
Геометрическая оптика
Геометри́ческая о́птика — раздел оптики, изучающий законы распространения света в прозрачных средах и принципы построения изображений при прохождении света в оптических системах без учёта его волновых свойств.
Краеугольным приближением геометрической оптики является понятие светового луча. В этом определении подразумевается, что направление потока лучистой энергии (ход светового луча) не зависит от поперечных размеров пучка света.
В силу того, что свет представляет собой волновое явление, имеет место интерференция, в результате которой ограниченный пучок света распространяется не в каком-то одном направлении, а имеет конечное угловое распределение т.е имеет место дифракция. Однако в тех случаях, когда характерные поперечные размеры пучков света достаточно велики по сравнению с длиной волны, можно пренебречь расходимостью пучка света и считать, что он распространяется в одном единственном направлении: вдоль светового луча.
Кроме отсутствия волновых эффектов, в геометрической оптике пренебрегают также квантовыми эффектами. Как правило, скорость распространения света считается бесконечной (вследствие чего динамическая физическая задача превращается в геометрическую), однако учёт конечной скорости света в рамках геометрической оптики (например, в астрофизических приложениях) не представляет трудности. Кроме того, как правило, не рассматриваются эффекты, связанные с откликом среды на прохождение лучей света. Эффекты такого рода, даже формально лежащие в рамках геометрической оптики, относят к нелинейной оптике. В случае, когда интенсивность светового пучка, распространяющегося в данной среде, достаточно мала для того, чтобы можно было пренебречь нелинейными эффектами, геометрическая оптика базируется на общем для всех разделов оптики фундаментальном законе о независимом распространении лучей. Согласно нему лучи при встрече с другими лучами продолжает распространяться в том же направлении, не изменив амплитуды, частоты, фазы и плоскости поляризации электрического вектора световой волны. В этом смысле лучи света не влияют друг на друга и распространяются независимо. Результирующая картина распределения интенсивности поля излучения во времени и пространстве при взаимодействии лучей может быть объяснена явлением интерференции.
Не учитывает геометрическая оптика также и поперечного характера световой волны. Вследствие этого в геометрической оптике не рассматривается поляризация света и связанные с ней эффекты.
Содержание
Законы геометрической оптики
В основе геометрической оптики лежат несколько простых эмпирических законов:
Поскольку геометрическая оптика не учитывает волновой природы света, в ней действует постулат, согласно которому если в какой-то точке сходятся две (или большее количество) систем лучей, то освещённости, создаваемые ими, складываются.
Однако наиболее последовательным является вывод законов геометрической оптики из волновой оптики в эйкональном приближении. В этом случае, основным уравнением геометрической оптики становится уравнение эйконала, которое допускает также словесную интерпретацию в виде принципа Ферма, из которого и выводятся перечисленные выше законы.
Частным видом геометрической оптики является матричная оптика.
Разделы геометрической оптики
Среди разделов геометрической оптики стоит отметить
История исследований
Евклид в «Оптике» показал прямолинейность распространения света.
Клавдий Птолемей исследовал преломление света на границе воздух—вода и воздух—стекло. Большую роль в развитии оптики, как науки сыграли ученые Востока, такими как ученые Азербайджана Бахманияр аль Азербайджани и Насреддин Туси. Они также имели свой взгляд на природу света и указывали, что свет имеет как свойства волны, так и свойства потока частиц. Арабский учёный Ибн ал-Хайсам (Аль-Гасан) изучал законы преломления и отражения света. Одним из первых высказал мысль о том, что источником световых лучей является не глаз, а светящиеся предметы. Он также в частности доказал, что изображение предмета возникает в хрусталике глаза. Он сумел получить изображения предметов в плоских, выпуклых, вогнутых, цилиндрических стеклах и линзах, а также показал, что выпуклая линза дает увеличенное изображение.
Иоганн Кеплер в трактате «Дополнения к Виттелию» («Оптическая астрономия», 1604) изложил основы геометрической оптики, сформулировал закон об обратно пропорциональной зависимости освещённости и квадрата расстояния от источника.
Геометрическая оптика
Основное понятие геометрической оптики — это световой луч. При этом подразумевается, что направление потока лучистой энергии (ход светового луча) не зависит от поперечных размеров пучка света.
Законы геометрической оптики являются частным предельным случаем более общих законов волновой оптики, в предельном случае стремления длины световых волн к нулю. Так как свет физически является распространением электромагнитной волны, происходит интерференция, в результате которой ограниченный пучок света распространяется не в каком-то одном направлении, а имеет конечное угловое распределение т. е. наблюдается дифракция. Интерференция и дифракция находятся вне предмета изучения оптических свойств оптических систем средствами геометрической оптики. Однако, в тех случаях, когда характерные поперечные размеры пучков света достаточно велики по сравнению с длиной волны, можно пренебречь дифракционной расходимостью пучка света и считать, что лучи света распространяются по отрезкам прямых, до преломления или отражения.
Помимо пренебрежения волновыми эффектами в геометрической оптике также пренебрегают квантовыми явлениями. В геометрической оптике скорость распространения света считается бесконечной (поэтому динамическая физическая задача превращается в чисто геометрическую), однако учёт конечной скорости света в рамках геометрической оптики (например, в астрофизических приложениях) не представляет математической трудности. Кроме того, как правило, не рассматриваются эффекты, связанные с влиянием прохождения света через оптические среды, например, изменения показателя преломления среды под воздействием мощного излучения. Эти эффекты, даже формально лежащие в рамках геометрической оптики, относят к нелинейной оптике. В случае, когда интенсивность светового пучка, распространяющегося в данной среде, достаточно мала для того, чтобы можно было пренебречь нелинейными эффектами, геометрическая оптика базируется на общем для всех разделов оптики фундаментальном законе о независимом распространении лучей (принцип суперпозиции).
Согласно этому принципу, лучи света в среде не взаимодействуют. В геометрической оптике нет таких понятий, как амплитуда, частота, фаза и вид поляризации светового излучения, но и в волновой линейной оптике постулируют принцип суперпозиции. Иными словами, и в волновой линейной оптике, и в геометрической оптике принимается, что лучи света и оптические волны не влияют друг на друга и распространяются независимо.
ГЕОМЕТРИЧЕСКАЯ ОПТИКА
1. Закон прямолинейного распространения света: в однородной среде свет распространяется прямолинейно. Линия, вдоль к-рой переносится световая энергия, наз. лучом. В однородной среде лучи света представляют собой прямые линии.
2. Закон преломления, к-рый устанавливает изменение направления луча при переходе из одной однородной среды в другую: падающий и преломлённый лучи лежат в одной плоскости с нормалью к преломляющей поверхности в точке падения, а направления этих лучей связаны соотношением пsin 


3. Закон отражения, к-рый устанавливает изменение направления луча в результате встречи с отражающей (зеркальной) поверхностью: падающий и отражённый лучи лежат в одной плоскости с нормалью к отражающей поверхности в точке падения, и эта нормаль делит угол между лучами на две равные части. Формально этот закон можно рассматривать как частный случай закона преломления при n‘=- п. Закон отражения впервые упоминается в «Катоптрике» Евклида (примерно 300 до н. э.).
4. Закон независимого распространения лучей: отд. лучи не влияют друг на друга и распространяются независимо. Если в какой-либо точке сходятся две системы лучей, то освещённости, создаваемые ими, складываются.
оптич. оси. Коэф. подобия фигур равен абс. значению линейного увеличения оптич. системы (см. Увеличение оптическое). Осн. понятиями параксиальной оптики, или теории идеальных оптич. систем, являются кардинальные точки оптической системы. Ограниченные поперечные размеры входных отверстий оптич. систем приводят к ограничению как телесного угла пучков лучей, исходящих из отд. точек предмета, так и к ограничению изображаемого пространства. С ограничением пучков лучей в оптич. системах связаны такие понятия Г. о., как апертурная и полевая диафрагмы, входной и выходной зрачки, апертурный и полевой углы, числовая апертура.
Лит.: Тудоровский А. И., Теория оптических приборов, 2 изд., ч. 1, M.- Л., 1948; Слюсарев Г. Г., Методы расчета оптических систем, 2 изд., Л., 1969; Герцбергер M., Современная геометрическая оптика, пер. с англ., M.. 1962; Чуриловский В. H., Теория оптических приборов, M.- Л., 1966; ГОСТ 7427-76. Геометрическая оптика. Термины, определения и буквенные обозначения.
Естествознание. 11 класс
Конспект урока
Естествознание, 11 класс
Урок 15. Геометрическая оптика и оптические приборы
Перечень вопросов, рассматриваемых в теме:
Геометри́ческая о́птика – раздел оптики, изучающий законы распространения света в прозрачных средах, отражения света от зеркально-отражающих поверхностей и принципы построения изображений при прохождении света в оптических системах без учёта его волновых свойств.
Объектив – это система, состоящая из нескольких линз.
Все параллельные лучи, перпендикулярные плоскости линзы объектива после прохождения объектива сводятся в одну точку на определенном расстоянии от задней части объектива. Эта точка называется фокусом (точкой фокусировки), а расстояние от фокуса до линзы (системы линз) называется фокусным расстоянием. Лучи, идущие от некоторого точечного источника света, после прохождения объектива также сходятся в одной точке, положение которой определяется правилами построения изображения в линзе. Точка, в которой сходятся лучи, называется изображением исходной точки. Построение изображения любого протяженного объекта получается как построение отдельных точек, на которые можно разбить объект.
Проектор – приборы, увеличивающие изображение и демонстрирующие на экран.
Способность изменять фокусное расстояние называется аккомодацией.
Лупа – оптическая система, состоящая из линзы или нескольких линз, предназначенная для увеличения и наблюдения мелких предметов, расположенных на конечном расстоянии.
Окуляр – элемент оптической системы, обращённый к глазу наблюдателя, часть оптического прибора (видоискателя, дальномера, бинокля, микроскопа, телескопа и так далее), предназначенная для рассматривания изображения, формируемого объективом или главным зеркалом прибора.
Основная и дополнительная литература по теме урока:
Теоретический материал для самостоятельного изучения
Сейчас трудно себе представить жизнь без оптических приборов, позволяющих проникнуть вглубь тел и раскрыть тайны мироздания, а также ввысь, рассматривая удаленные небесные тела и любуясь стереоизображениями. На каких принципах основаны эти приборы? Как они помогают человеку в современном мире?
Например, микроско́п (греч.Μικρός «маленький» + σκοπέω «смотрю») — прибор, предназначенный для получения увеличенных изображений, а также измерения объектов или деталей структуры, невидимых или плохо видимых невооружённым глазом, появление которого относят к 1590г. Трудно теперь представить жизнь без его существования.
Являясь электромагнитной волной, свет долгое время не был изучен по причине малой длины волны видимого излучения.
Поэтому такие волновые явления как интерференция и дифракция в обычных условиях практически не проявляются.
И даже Ньютон предполагал, что свет представляет собой поток частиц. Предполагалось, что эти частицы двигаются от одного предмета до другого по прямой линии, а потоки этих частиц образуют лучи, которые можно наблюдать, пропустив свет через маленькое отверстие. Такое рассмотрение получило название геометрическая оптика, в отличие от волновой оптики, где свет рассматривается как волна.
Геометрическая оптика позволила обосновать законы отражения света и преломления света на границе между различными прозрачными веществами. В результате были объяснены свойства линз, которые вы изучали в курсе физики. Именно с изобретения линз началось практическое использование достижений оптики.
В основе геометрической оптики лежат четыре основных
1. Закон независимости световых лучей.
2. Закон прямолинейного распространения света.
3. Закон отражения света.
4. Закон преломления света.
Построение изображения в собирающей линзе:
Расстояние от источника до линзы d связано с расстоянием от изображения до линзы d′ соотношением: 1/d + 1/d′ = 1/f, где f – фокусное расстояние, то есть расстояние от фокуса линзы до линзы. Изображение объекта может быть как уменьшенным, так и увеличенным. Коэффициент увеличения (уменьшения) несложно получить, исходя из Рис. 1 и свойств подобия треугольников: Г = d′/d. Из двух последних формул можно вывести следующее свойство: изображение получается уменьшенным, если d>2f (в этом случае f 2f). Если необходимо значительно увеличить изображение, тогда объект нужно поместить на расстоянии от линзы чуть дальше фокуса, изображение будет отстоять на большом расстоянии от линзы. Напротив, если нужно значительно уменьшить изображение, то объект помещают на большом расстоянии от линзы, а его изображение будет находиться чуть дальше, чем фокус от линзы. В качестве объективов в телескопах используются также вогнутые зеркала. Свойства вогнутого зеркала во многом подобны свойствам собирающей линзы, только изображение создается не за зеркалом, а перед зеркалом (Рис. 2). Это как бы отражение изображения, полученного линзой.
Описанное свойство линз используется в различных приборах, где собирающие линзы применяются в качестве объективов. Строго говоря, любой качественный объектив состоит из системы линз, однако его действие такое же, как у одной собирающей линзы.
Приборы, увеличивающее изображение называются проекторами. Проекторы используются, например, в кинотеатрах, где изображение на пленке с размерами в несколько сантиметров увеличивается до размеров экрана в несколько метров. Другой тип проекторов – мультимедийные проекторы. В них сигнал, поступающий с компьютера, видеомагнитофона, устройства записи изображения на видеодисках формирует малое изображение, которое через объектив проектируется на большой экран.
Часто необходимо уменьшить, а не увеличить изображение. Для этого служат объективы в фотоаппаратах и видеокамерах. Изображение в несколько метров, например, изображение человека, уменьшается до размеров в несколько сантиметров или в несколько миллиметров. Приемником, куда проецируется изображение, является фотопленка или специальная матрица из полупроводниковых датчиков (ПЗС-матрица), преобразующая видеоизображение в электрический сигнал.
Уменьшение изображения позволяют производить микросхемы, применяемые в электронных устройствах, в частности в компьютерах. Элементы микросхем – полупроводниковые приборы, соединительные провода и др. имеют размеры в несколько микрометров, а их число на кремниевой пластинке с размерами порядка сантиметра достигает нескольких миллионов. Естественно, нарисовать столько элементов такого масштаба без уменьшения при помощи объектива невозможно.
Наш глаз также содержит в своем составе объектив – хрусталик, уменьшающий видимые нами объекты до размеров сетчатки глаза – несколько миллиметров
Чтобы изображение было резким, специальные мышцы изменяют фокусное расстояние хрусталика, увеличивая его при приближении объекта и уменьшая при удалении. Способность изменять фокусное расстояние называется аккомодацией. Нормальный глаз способен фокусировать изображение для объектов, находящихся далее 12 см от глаза. Если мышцы не способны уменьшить фокусное расстояние хрусталика до требуемой величины, человек не видит близкие предметы, то есть страдает дальнозоркостью. Исправить положение можно, поместив перед глазом собирающую линзу (очки), действие которой эквивалентно уменьшению фокусного расстояния хрусталика. Исправление противоположного дефекта зрения – близорукости происходит при помощи рассеивающей линзы в очках.
При помощи глаза мы можем оценить только угловые размеры объекта. Например, булавочной головкой мы можем закрыть изображение Луны, то есть угловые размеры Луны и булавочной головки можно сделать одинаковыми. Добиться визуального увеличения можно либо приблизив объект к глазу, либо каким-то способом увеличив его на том же расстоянии от глаза.
Стараясь рассмотреть какой-то мелкий объект, мы приближаем его к глазу. Однако при очень сильном приближении наш хрусталик не справляется с работой, фокусное расстояние не может уменьшиться так, чтобы мы могли рассмотреть объект, например, с расстояния 5 см. Исправить положение можно так же, как и при дальнозоркости, поместив перед глазом собирающую линзу. Использующая с этой целью линза называется лупой. Расстояние, с которого нормальному глазу удобно рассматривать мелкий объект называется расстояние наилучшего зрения. Обычно это расстояние принимается равным 25 см. Если лупа позволяет рассмотреть объект например, с расстояния 5 см., то достигается визуальное увеличение в 25/5=5 раз.
А как получить визуальное увеличение, например, Луны? При помощи объектива нужно создать уменьшенное, но приближенное к глазу изображение Луны, а затем рассмотреть это изображение в лупу, которая в данном случае называется окуляр. Именно так работает труба Кеплера. Недостаток трубы Кеплера, заключающийся в том, что в ней изображение оказывается перевернутым, отсутствует в изобретенном Галилеем телескопе (труба Галилея). В качестве окуляра в трубе Галилея в отличие от трубы Кеплера используется рассеивающая линза.
Визуальное увеличение, например, клетки растения или животного получается другим образом. Объектив создает увеличенное изображение объекта, близкое к глазу, которое рассматривается в окуляр. Именно так работает микроскоп.
Примеры и разбор решения заданий тренировочного модуля:
Варианты ответов: электромагнитные, 0,4; 0,8; магнитные, 0,2; 1,2.
Правильный вариант: Свет – это электромагнитные волны, вызывающие зрительное ощущение. Их длина лежит в пределах от 0,4 до 0,8 мкм.
Задание 2. Добавьте подпись названий для каждой модели оптического устройства.
Правильный вариант: Объектив – Рис.1, Проектор – Рис.2, Лупа – Рис.3
Содержание:
Геометрическая оптика – это раздел оптики, в котором изучаются законы распространения световой энергии в прозрачных средах на основе представления о световом луче. Световой луч – это линия, имеющая направление, вдоль которого распространяется энергия световых волн.
Закон отражения света с точки зрения корпускулярной и волновой теории
Если луч света состоит из частиц, как утверждал И. Ньютон, то можно полагать, что они отражаются от поверхности, как упругие мячи (рис. 149) в соответствии с законом отражения, изученным в геометрической оптике.
К такому же выводу приводит и волновая теория, основанная на принципе Х. Гюйгенса: каждая точка среды, до которой дошло возмущение, является источником вторичных волн. Огибающая фронты вторичных волн является фронтом результирующей волны (§ 11).
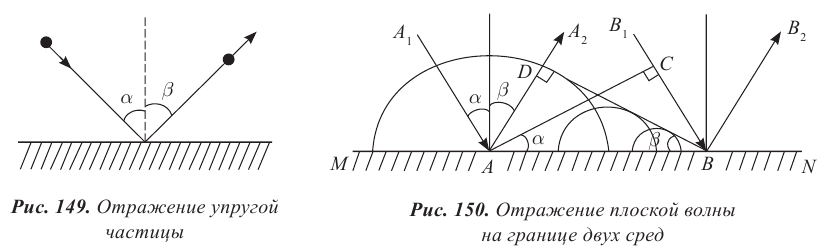
Рассмотрим отражение плоской волны от поверхности MN (рис. 150). Лучи
Поскольку рассматриваемые треугольники равны, то углы 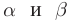
Запомните! Закон отражения: Угол падения равен углу отражения 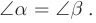
На основе волновой теории можно объяснить, почему свет почти не отражается от поверхности толстого стекла и практически полностью отражается от тончайшей металлической фольги. Стекло – диэлектрик, в нем нет свободных заряженных частиц, он прозрачен для электромагнитных волн. В металлах свободные электроны под действием световой волны совершают колебательные движения, созданное ими поле отражает световую волну.
Применение закона отражения
Закон отражения получил применение в различных устройствах и аттракционах.
На транспорте применяется угловой отражатель – катафот, изготовленный из стекла или пластмассы. Сзади велосипеда укрепляют красный, впереди – белый, на спицах колес – оранжевый. Светоотражатель направляет луч света обратно к освещающему его источнику независимо от угла падения света на поверхность. Ими оборудуются все транспортные средства и опасные участки дорог. Светосигнальные приборы европейского образца появились на автодорогах республиканского значения, их установили на участках «Алматы – Ташкент – Термез», «Новый обход перевала Куюк» в Жамбылской области (рис. 151). Приборы заряжаются солнечными лучами, и они освещают осевую линию дороги в темное время суток. Установлены сигнальные столбики с надписью «Kazautozhol» на автомобильных дорогах, где нет искусственного освещения.
Светоотражающие материалы используются для пошива спецодежды – костюмов для работников пожарных, медицинских, военных и других видов служб. Существует два вида светоотражателей: на текстильной и основе ПВХ. Светоотражатели на текстильной основе производят с использованием стеклянных микрошариков с алюминиевым слоем отражателя, которые наносятся на рабочую поверхность материал полимерным клеем. Светоотражатели на основе ПВХ производят с использованием микропирамидок. Они превосходят светоотражатели на текстильной основе в износостойкости, поскольку микропирамидки находятся изнутри пленки.
Формула плоского зеркала
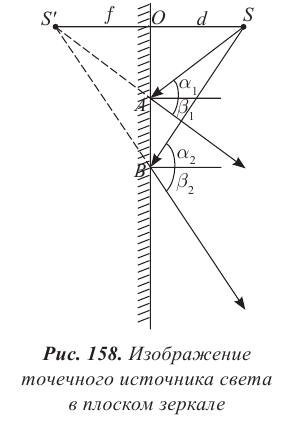
Запишем формулу плоского зеркала в соответствии с изображением, полученным на рисунке 158:
где d − расстояние от предмета до зеркала; 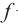
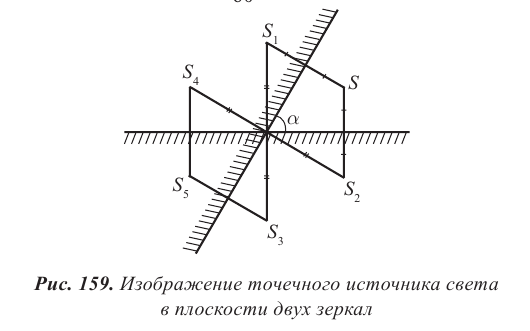
Изображение в двух плоских зеркалах
С помощью двух плоских зеркал можно получить несколько изображений, число которых определяется углом между отражающими поверхностями зеркал 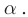
Например, при 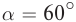
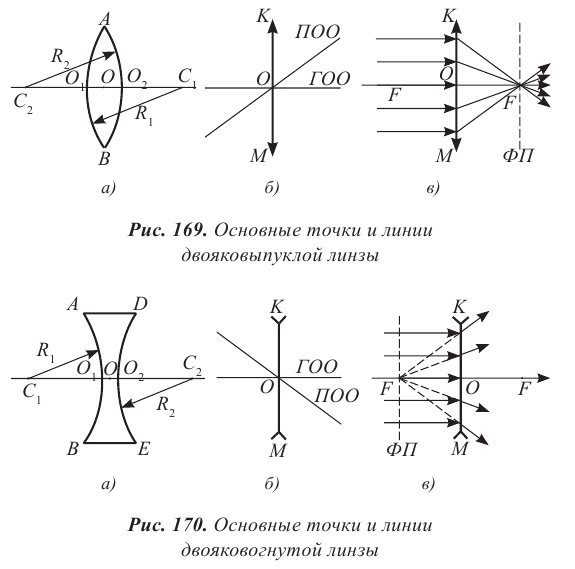
Сферические зеркала. Основные точки и линии зеркал
Зеркала, отражающая поверхность которых представляет собой часть сферы, называют сферическими.
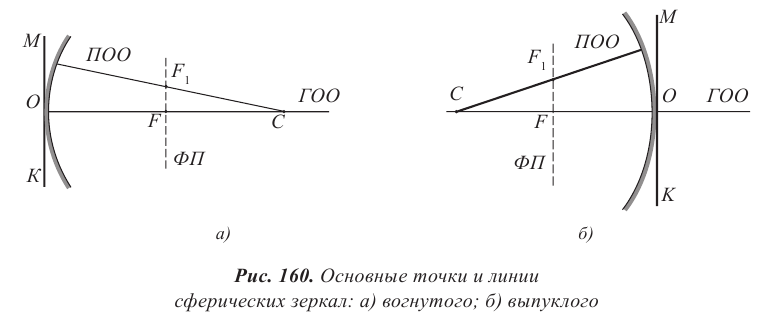
Основные точки и линии зеркал: вершина зеркала – точка O; центр кривизны – точка C; главная оптическая ось (ГОО) − прямая, проходящая через вершину и центр зеркала; фокус зеркала – точка F, в которой фокусируются все лучи, падающие на плоскость зеркала параллельно ГОО (рис. 160). Фокус выпуклого зеркала мнимый, он находится за плоскостью зеркала.
Введем еще несколько основных точек и линий для сферических зеркал. Побочная оптическая ось (ПОО) – прямая, проходящая через центр кривизны зеркала С. Фокус побочной оптической оси F1 находится в точке пересечения ПОО с фокальной плоскостью (ФП). Через эту точку проходят лучи, параллельные ПОО. Фокальная плоскость – это плоскость, перпендикулярная главной оптической оси и проходящая через ее фокус. МК – главная плоскость сферического зеркала – это плоскость, перпендикулярная ГОО и проходящая через вершину зеркала.
Формула вогнутого сферического зеркала
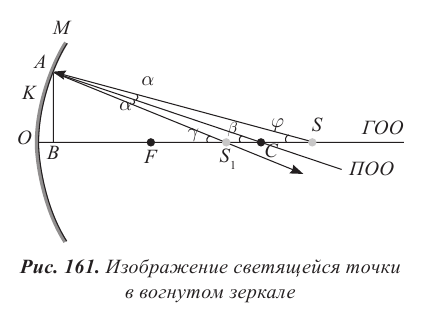
Формула вогнутого сферического зеркала справедлива для параксиальных лучей, которые составляют с главной оптической осью малые углы. При таком условии фокальная плоскость перпендикулярна главной оптической оси. На рисунке 161 изображен луч источника света S, он отражается от точки A поверхности вогнутого зеркала.
KM − касательная в точке А, перпендикулярная радиусу AC или побочной оптической оси. Для параксиальных лучей можно считать, что: 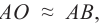
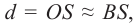
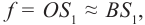
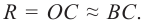
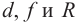
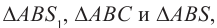
Установим связь между углами треугольников. Угол 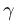
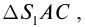
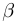
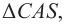
Из (5) выразим 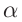
Тангенсы малых углов равны значениям углов в радианной мере. Выразим тангенсы из уравнений (3) и, подставив в уравнение (6), получим формулу сферического зеркала:
Построение изображения предмета в сферическом зеркале
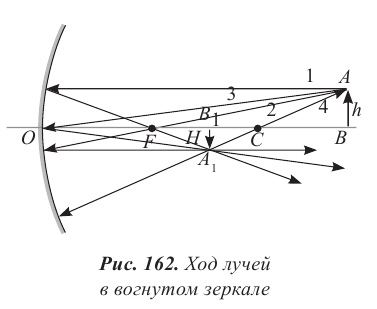
Для построения изображения в сферическом зеркале достаточно использовать два луча из тех, ход которых известен (рис. 162):
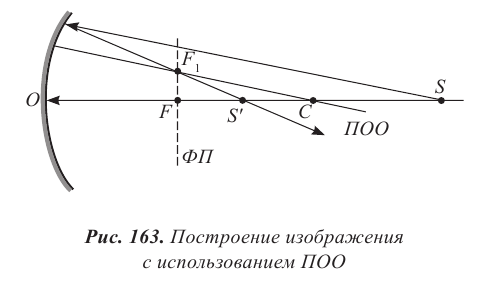
Алгоритм построения изображения точечного источника света
1. Провести ПОО, указать в точке пересечения с ФП фокус проведенной оси (рис. 163).
2. От источника света S построить луч, параллельный ПОО, до главной плоскости зеркала. Провести отраженный луч через фокус побочной оси.
3. Указать в точке пересечения с лучом, направленным вдоль ГОО, полученное изображение
Вспомните! Изображение мнимое, если пересекаются не сами отраженные лучи, а их продолжения. Изображение предмета действительное, если пересекаются лучи.
Линейное увеличение
Рассчитать изменение линейных размеров тела можно из подобия треугольников 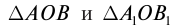
где H − высота изображения; h − высота предмета; 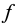
Физическую величину, равную отношению высоты изображения к высоте предмета, называют линейным увеличением зеркала.
Если 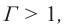
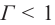
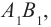
Закон преломления света с точки зрения волновой теории
Закон преломления света открыт экспериментально голландским математиком В. Снеллиусом в начале XVII в.
Произведение абсолютного показателя преломления на синус угла падения остается постоянной величиной, являясь «оптическим инвариантом» при переходе света из одной среды в другую.
где 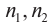
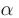
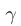
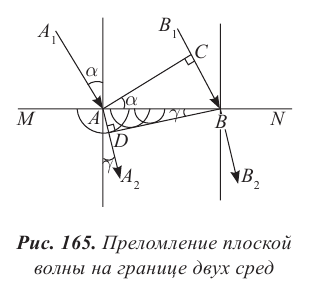
Рассмотрим преломление двух лучей 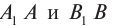
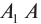
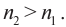
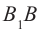
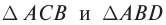
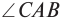
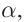
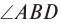
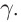
Из формул (3) и (4) следует, что:
Выразим скорость света в средах через абсолютный показатель преломления:
Вспомните! Абсолютный показатель преломления – это физическая величина, показывающая, во сколько раз скорость распространения света в вакууме больше скорости распространения света в данной среде: 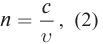
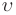
Подставив формулы (6) в (5), получим:
На основе волновой теории Гюйгенса получен закон преломления Снеллиуса.
Вспомните! Относительный показатель преломления – это физическая величина, которая показывает во сколько раз скорость распространения света в первой среде больше скорости распространения света во второй среде.
Заменим в уравнении (7) отношение абсолютных показателей преломления относительным показателем, получим:
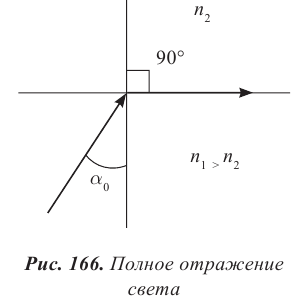
Полное внутреннее отражение света
Если направить луч света из оптически более плотной среды в менее плотную среду, то угол преломления больше угла падения. Наибольшему значению угла преломления, равному 90º, соответствует угол падения 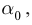
При падении луча на границу сред под углом, превышающим предельный угол полного внутреннего отражения 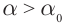
Закон преломления для предельного угла примет вид:
Из полученного равенства следует, что предельный угол полного отражения определяется показателем преломления среды в том случае, если второй средой является вакуум или воздух:
Запомните! Закон преломления света:
Отношение синуса угла падения к синусу угла преломления для двух сред есть величина постоянная. Она равна относительному показателю преломления второй среды относительно первой.
Луч падающий, луч преломленный и перпендикуляр восстановленный в точку падения луча к границе раздела двух сред, лежат в одной плоскости.
Преимущества оптоволоконной технологии при передаче световых сигналов
Простейшая оптоволоконная система передачи информации между двумя точками состоит из трех основных элементов: оптического передатчика, оптоволоконного кабеля и оптического приемника.
Оптический передатчик преобразует электрический сигнал в модулированный световой поток, предназначенный для передачи по оптоволокну. В качестве источника света используются светодиоды и полупроводниковые лазеры. Длина волны излучения выбрана с учетом максимальной прозрачности материала волокна и наивысшей чувствительности фотодиодов. Оптические передатчики работают в диапазоне инфракрасных лучей с длиной волны 850, 1300 и 1550 нм.
Оптический приемник преобразует световой сигнал в копию исходного электрического сигнала. В качестве чувствительного элемента оптического приемника используется фотодиод.
Световод (оптоволоконный кабель) − закрытое устройство для направленной передачи света.
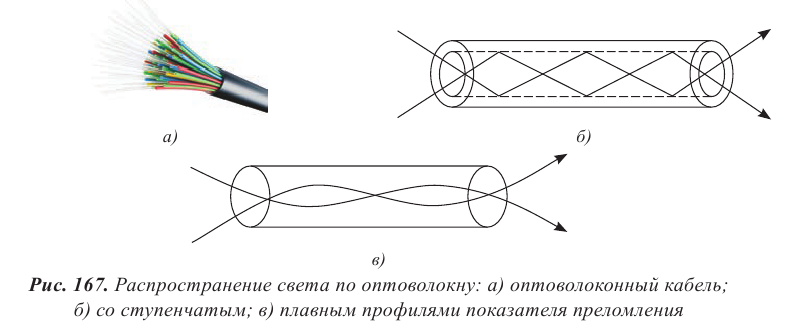
Оптоволоконный кабель состоит из одного или нескольких стеклянных волокон со ступенчатым или плавным изменением показателя преломления вдоль радиуса (рис. 167 а). Волокно со ступенчатым профилем показателя преломления состоит из сердцевины, изготовленной из стекла с малыми оптическими потерями, окруженной стеклянной оболочкой с более низким показателем преломления (рис. 167 б). Оптоволокно с плавным профилем состоит из стекла только одного сорта, но оно обработано так, что его показатель преломления плавно уменьшается от центра к поверхности волокна. Такой световод постоянно отклоняет распространяющийся по нему свет к центру (рис. 167 в).
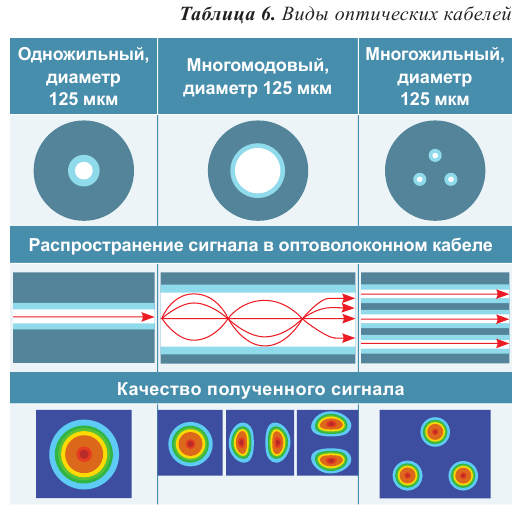
В зависимости от числа волокон различают кабели одножильные, многожильные и многомодовые, которые позволяют распространяться световым волнам по нескольким различным путям, которые называют модами.
В многомодовых волокнах каждая световая волна распространяются под своим углом. Волны по-разному отражаются от оболочки и поступают в приемник в разное время. В одном многомодовом кабеле может быть порядка 80–100 мод. В многожильных кабелях возможно использование нескольких отдельных волокон, диаметр которых колеблется от 8 мкм до 10 мкм, соответствует диаметру одножильных кабелей. Многомодовые и многожильные кабели в сравнении с одножильными кабелями обеспечивают большую пропускную способность на малые расстояния, около 2 метров, на больших дистанциях возникают помехи. Одножильное оптоволокно чаще всего применяется в телекоммуникационных системах большой протяженности.
Оптические кабели имеют ряд преимуществ над обычными проводами и кабелями:
Интересно знать! В настоящее время используются оптоволоконные кабели, позволяющие передавать данные на большие расстояния с пропускной способностью до 100 Гбит/с. Максимальная пропускная способность оптоволоконного кабеля со спектральным уплотнением каналов WDM достигает 9,6 Тбит/с, так как он способен передать данные одновременно по 96 каналам.
Построение изображения в системе линз. Формула тонкой линзы
I. Собирающая и рассеивающая линзы
Линза представляет собой прозрачное тело, ограниченное с двух сторон сферическими поверхностями: 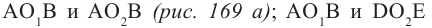
Обратите внимание! Если показатель преломления линзы больше показателя преломления среды, то выпуклые линзы фокусируют падающие на них лучи, вогнутые линзы – рассеивают.
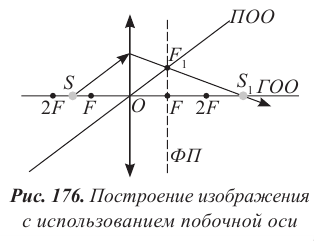
II. Ход лучей в собирающей и рассеивающей линзах
Луч 1, параллельный главной оптической оси, проходит через задний фокус линзы (рис. 171);
Луч 2, прошедший через центр линзы, не преломляется (рис. 171);
Луч 3, прошедший через передний фокус линзы, становится параллельным главной оптической оси (рис. 171);
Луч 4, прошедший через центр кривизны одной из сферической поверхностей, проходит через центр кривизны другой поверхности (рис. 171).
Обратите внимание! Зеркала дают изображение в отраженных лучах, а линзы – в проходящих.
III. Побочные оси. Построение лучей с использование побочных осей
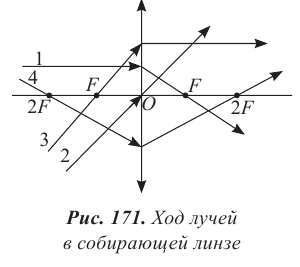
Фокусы побочных оптических осей F1 также принадлежат фокальной плоскости и находятся в точках пересечения ПОО с ФП (рис. 175 а). Лучи, падающие на собирающую линзу параллельно побочной оси, проходят через фокус ПОО (рис. 175 б). В рассеивающей линзе в фокусе побочной оси пересекаются продолжения лучей (рис. 175 в).
В том случае, когда предмет представляет собой точечный источник света, находящийся на главной оптической оси, для построения изображения используют побочную ось. На рисунке 176 изображен ход лучей при условии 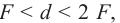
Запомните! Побочную ось необходимо ввести для лучей, падающих на линзу под произвольным углом. Она проводится параллельно падающему лучу. В этом случае преломленный луч пройдет через задний фокус побочной оси собирающей линзы (рис. 176). Для рассеивающей линзы необходимо провести преломленный луч таким образом, чтобы его продолжение прошло через передний фокус побочной оси.
IV. Формула тонкой линзы. Оптическая сила линзы. Увеличение линзы
Формула тонкой линзы вам известна из курса физики 8 класса:
где D – оптическая сила линзы. Для собирающей линзы фокус линзы положительный F > 0, для рассеивающей линзы – отрицательный F 1, если изображение уменьшенное, то Г 0, для мнимого предмета d D), т. е. проявляется волновой характер светового излучения. Следует отметить, что дифракция будет наблюдаться на очень больших расстояниях от экрана 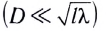
Таким образом, луч — чисто геометрическое понятие. Луч указывает направление, перпендикулярное фронту волны, в котором опа переносит энергию.
Лучи, выходящие из одной точки, называют расходящимися, а собирающиеся в одной точке — сходящимися. Примером расходящихся лучей может служить любой точечный источник света, а примером сходящихся — совокупность лучей, попадающих в зрачок нашего глаза от различных предметов.
Пересекающиеся световые лучи не взаимодействуют друг с другом в рамках геометрической оптики, т. е. «исказить» изображение с помощью других лучей невозможно. Факт независимости распространения световых лучей от наличия (или отсутствия) других лучей устанавливается в следующем законе геометрической оптики.
Закон независимости световых лучей:
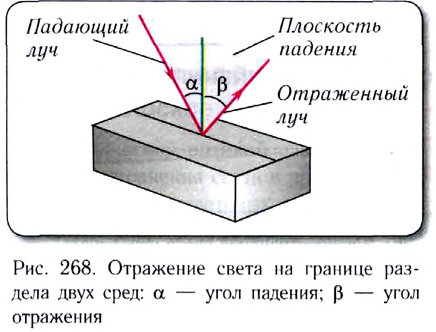
Целый ряд оптических явлений (отражение облаков в воде, отражение предметов в зеркальной или любой полированной поверхности и т. д.) способствовали открытию следующего закона геометрической оптики — закона отражения света (рис. 268):
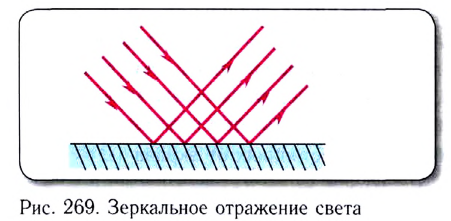
Эксперименты показывают, что существуют два вида отражения света: зеркальное и рассеянное. Поверхность, размеры неровностей которой меньше длины световой волны, называют зеркальной. Лучи света, падающие на такую плоскую поверхность параллельным пучком, после отражения остаются параллельными. Такое отражение называют зеркальным (рис. 269).
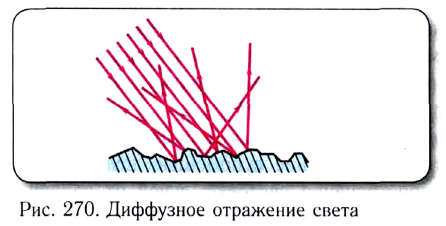
Поверхность, размеры неровностей которой больше длины световой волны, отражает лучи света по всевозможным направлениям и называется шероховатой, а отраженный свет — рассеянным или диффузным (рис. 270).
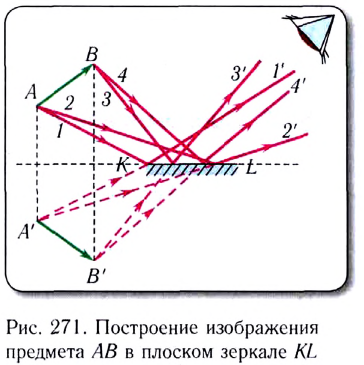
Используя закон отражения света, можно построить изображение предмета АВ в плоском зеркале (рис. 271), представляющем собой плоскую отражающую поверхность. Построив ход лучей 1 и 2 от точки А после отражения от зеркала KL, продолжим их до пересечения в точке А’. Аналогичные построения
сделаем для точки В, найдем ее изображение — точку В’. Глазу наблюдателя будет казаться, что лучи вышли из точек А’ и В’, т. е. оттуда, где будет находиться мнимое изображение А’В’ предмета АВ.
В оптике изображение называется действительным, если оно образовано самими лучами (т. е. в данную точку поступает световая энергия), если же изображение образовано не самими лучами, а их продолжениями, то говорят, что изображение мнимое (световая энергия не поступает в данную точку).
Изображение называется прямым, если верх и низ изображения ориентированы аналогично самому предмету. Если же изображение перевернуто, то его называют обратным или перевернутым.
Таким образом, изображение предмета в плоском зеркале — мнимое прямое, в натуральную величину. Оно симметрично предмету относительно плоскости зеркала и находится на таком же расстоянии за плоскостью зеркала, как и сам предмет (см. рис. 271).
Преломление света
Изменение направления распространения луча света при прохождении через границу раздела двух сред называется преломлением света.
Для наблюдения данного явления достаточно поместить карандаш в стакан с водой и посмотреть на него со стороны — карандаш будет казаться «надломленным» (преломленным) (рис. 273), оставаясь при этом совершенно целым.
Первые упоминания о преломлении света в воде и стекле встречаются в труде Клавдия Птолемея «Оптика», вышедшего в свет во II в. нашей эры.
Закон преломления света был экспериментально установлен в 1621 г. голландским ученым Виллебродом Снеллиусом и независимо от него теоретически обоснован в 1637 г. Рене Декартом.
Закон преломления световых лучей:
Здесь 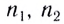
Рассмотрим луч, падающий на плоскую границу раздела двух прозрачных сред под некоторым углом 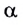
При этом наряду с отраженным лучом будет существовать и преломленный луч. Он распространяется во второй среде под некоторым углом у в соответствии с законом преломления.
Принцип Ферма
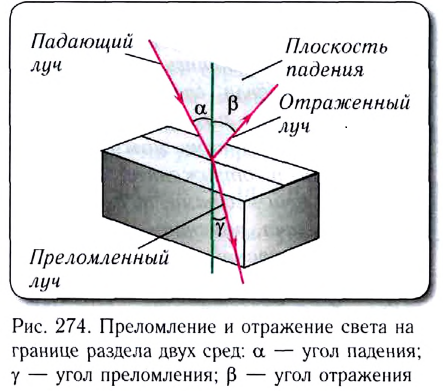
Хотя законы геометрической оптики были открыты экспериментально, однако все они (за исключением закона независимости световых лучей) являются следствием принципа «кратчайшего пути» или «минимального времени», сформулированного в 1679 г. французским математиком Пьером Ферма:
распространение света из одной точки среды в другую происходит по траектории, которой соответствует минимальное время по сравнению с другими возможными траекториями.
При помощи этого принципа Ферма вывел закон преломления света. Из этого принципа также следуют законы прямолинейного распространения и отражения света, т. е. принцип Ферма является наиболее общим принципом геометрической оптики.
Действительно, в однородной прозрачной среде, где скорость света постоянна 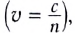
При отражении от плоского зеркала в силу симметрии можем сказать, что сумма |АВ| + |ВС| (рис. 275) будет минимальна в случае, когда 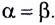
Впервые данный факт геометрически доказал Герон Александрийский (II в. н. э.) задолго до появления принципа Ферма.
Анализируя время распространения луча между двумя точками при преломлении света, можно показать, что принцип Ферма выполняется и в этом случае, т. е. при движении по «траектории» преломления свету потребуется наименьшее время но сравнению с любой другой возможной «траекторией».
Для законов отражения и преломления выполняется принцип обратимости световых лучей:
На границе раздела двух прозрачных сред обычно одновременно с преломлением наблюдается отражение волн.
Согласно закону сохранения энергии сумма энергий отраженной 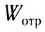
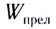
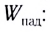
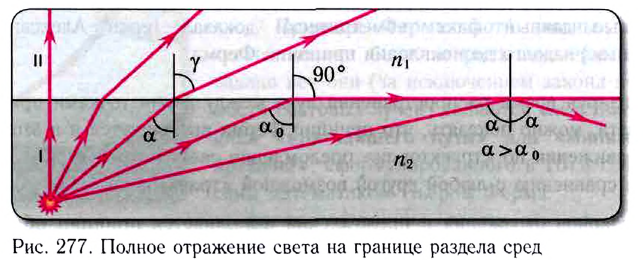
Примерный баланс энергий между отраженной и преломленной волнами приведен на рисунке 276.
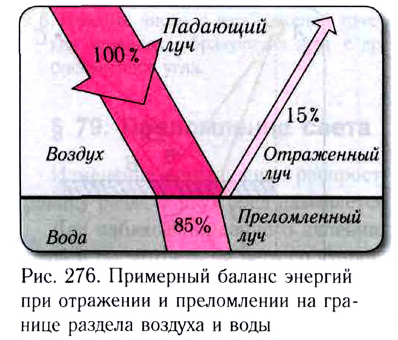
Как следует из закона преломления, при переходе света из оптически более плотной среды I (с большим абсолютным показателем преломления 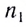
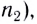
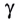
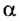
По мере увеличения угла падения, при некотором его значении 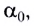
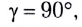
Энергия преломленной волны при этом станет равной нулю, а энергия отраженной волны будет равна энергии падающей. Следовательно, начиная с этого угла падения вся световая энергия отражается от границы раздела этих сред в среду I.
Это явление называется полным отражением (см. рис. 277). Угол 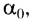
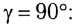
Таким образом, при углах падения, больших 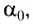
Закон преломления света позволяет определять ход лучей в различных оптических системах.
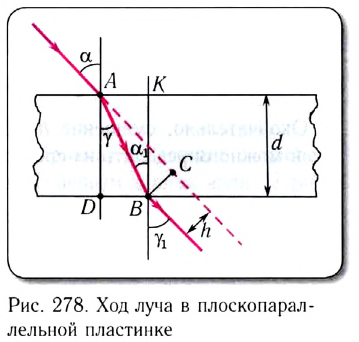
На рисунке 278 показан ход светового луча в плоскопараллельной пластинке толщиной d, находящейся в воздухе. Согласно закону преломления на первой и второй границах раздела для луча, падающего под углом 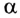
Здесь 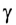
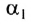
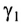
Накрест лежащие углы 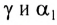
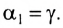
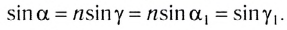
Таким образом, луч света, проходя через плоскопараллельную пластинку, с обеих сторон которой находится одна и та же среда, смещается параллельно своему начальному направлению. Поэтому все предметы, если смотреть на них сквозь прозрачную плоскопараллельную пластинку под углом, не равным нулю, будут казаться смещенными на некоторое расстояние h. Найдем, от каких параметров пластинки зависит это смещение.
Из треугольника АВС следует, что
Из треугольника ABD находим
Из этих двух соотношений получаем
С учетом закона преломления 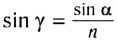
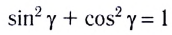
Окончательно, смещение h между направлениями входящего и выходящего лучей можно определить из соотношения
Откуда видно, что h при данном угле падения 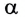
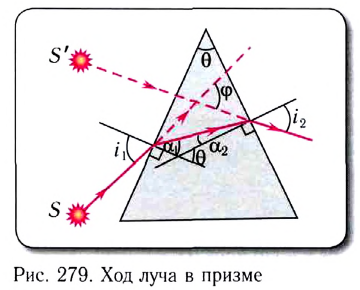
На рисунке 279 показан ход луча через стеклянную призму, находящуюся в воздухе. Грани, через которые проходит луч, называются преломляющими гранями; их ребро — преломляющим ребром, а угол 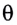
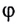
Если угол падения 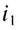
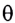
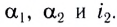
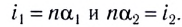
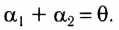
Из последнего равенства следует, что, во-первых, чем больше преломляющий угол 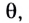
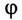
Знание наименьшего угла отклонения лучей призмой 
Направив пучок лучей белого света на призму, мы обнаружим его сложную структуру: на экране за призмой появится радужная полоска — спектр (рис. 280).
Образование спектра обусловлено тем, что призма, вследствие дисперсии, по-разному преломляет лучи, соответствующие различным длинам волн. Порядок следования лучей в спектре легко запомнить с помощью известной фразы:
Явление дисперсии совместно с полным отражением приводит к образованию радуги, вследствие преломления солнечных лучей на мельчайших водяных капельках во время дождя, к нежелательному «окрашиванию» изображений в оптических системах (хроматическая аберрация) и т. д.
Линза. Построение изображения в линзах
Линза называется собирающей, если после преломления в ней параллель-ный пучок становится сходящимся. Если же после преломления в линзе параллельный пучок становится расходящимся, то линза называется рассеивающей.
Как известно, плоское зеркало даст мнимое изображение предмета в натуральную величину. Однако для практических нужд чаще необходимы изображения увеличенные или уменьшенные. Эта задача решается с помощью линз (или криволинейных зеркал).
Линза представляет собой прозрачное тело, ограниченное с двух сторон криволинейными поверхностями. Чаще всего применяются линзы с поверхностями, имеющими сферическую форму (сферические сегменты).
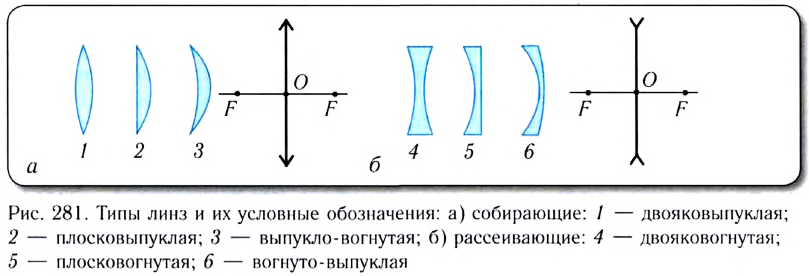
По форме ограничивающих поверхностей различают шесть типов линз. На рисунке 281, а. б показаны условные обозначения линз и типы линз.
Отметим условия, при одновременном выполнении которых линза является собирающей:
При невыполнении (или выполнении) только одного из этих условий линза является рассеивающей.
Линза считается тонкой, если ее толщина в центре намного меньше радиусов ограничивающих ее поверхностей. Тонкая линза дает неискаженное изображение только в том случае, если свет монохроматический и предмет достаточно мал, следовательно, лучи распространяются вблизи главной оптической оси. Такие лучи получили название параксиальных.
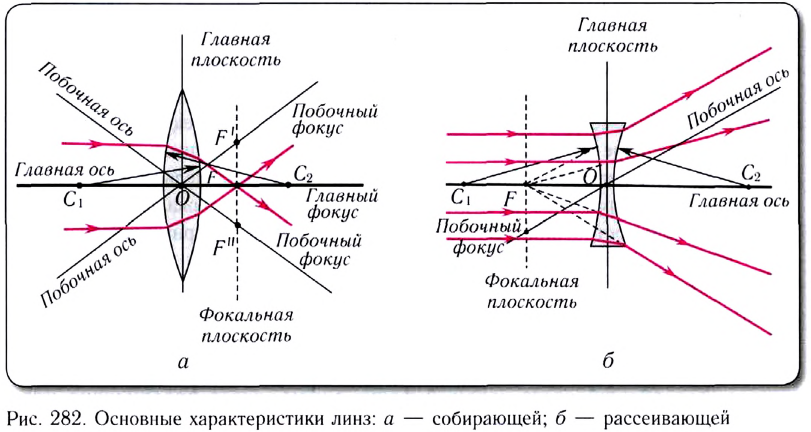
Рассмотрим основные характеристики линзы (рис. 282, а, б).
Прямая линия, на которой лежат центры 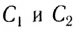
Точка О линзы, проходя через которую луч не преломляется, называется оптическим центром.
Прямая линия, проходящая через оптический центр линзы, не совпадающая с главной оптической осью, называется побочной оптической осью. Каждая линза имеет только одну главную оптическую ось и бесконечно много побочных осей.
Плоскость, проходящая через оптический центр тонкой линзы перпендикулярно главной оптической оси, называют главной плоскостью линзы.
Точка, в которую собирается параксиальный пучок света после преломления в линзе, распространяющийся параллельно главной оптической оси, называется главным фокусом F линзы. Расстояние OF от оптического центра линзы до се главного фокуса называется фокусным расстоянием линзы.
Плоскость, проходящая через главный фокус перпендикулярно главной оптической оси, называется фокальной плоскостью. Фокальная плоскость собирающей линзы является геометрическим местом точек, в которых пересекаются параллельные лучи, падающие на линзу под любым углом к главной оптической оси.
Пучок света, направленный на собирающую линзу параллельно побочной оптической оси, собирается в побочном фокусе, лежащем в фокальной плоскости.
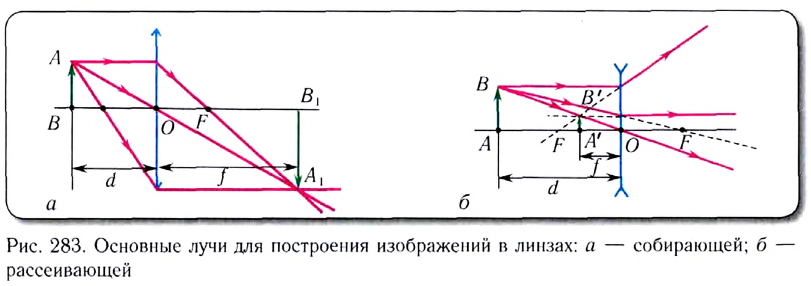
Обычно для построений в линзах используют три характерных (стандартных) луча (рис. 283, а, б):
Для построения изображения в линзе достаточно построить ход двух лучей от каждой точки предмета. Изображение находится в месте пересечения лучей после преломления на поверхностях линзы (действительное изображение) или в месте пересечения продолжений лучей (мнимое изображение).
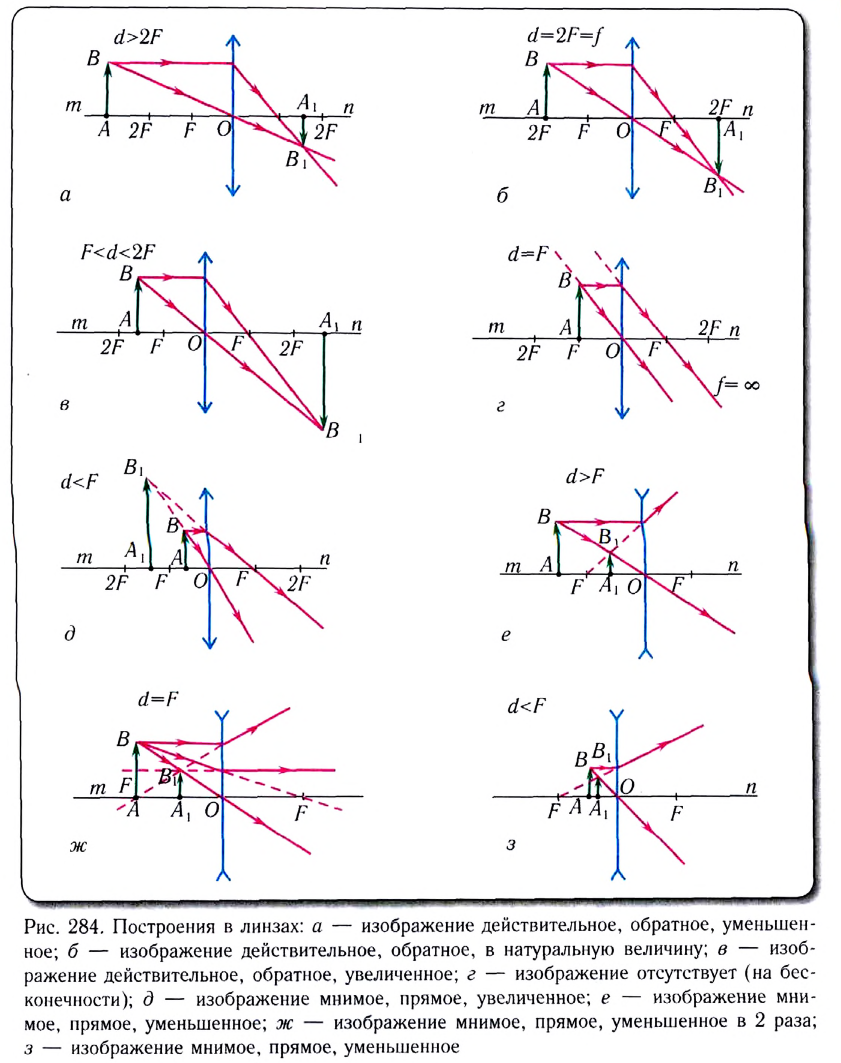
В зависимости от типа линзы и расстояния до нее можно получать изображения: увеличенные и уменьшенные, прямые и обратные (перевернутые), действительные и мнимые (рис. 284).
Все приведенные примеры построений относились к предметам, которые имели определенные размеры. А как найти построением положение изображения точечного источника света, находящегося на главной оптической оси?
Для этого необходимы два любых луча, один из которых — самый простой, — проходящий не преломляясь через оптический центр линзы. Для построения хода другого пользуются побочной оптической осью. Рассмотрим точечный источник, находящийся на главной оптической оси собирающей линзы (рис. 285). Проведем из точки S произвольный луч SA. Для того чтобы найти ход луча после преломления в линзе, проведем побочную оптическую ось 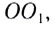
Точка пересечения побочной оптической оси 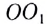
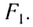
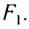
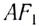
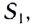
Положение изображения точечного источника, находящегося на главной оптической оси рассеивающей линзы, найдите построением самостоятельно.
Формула тонкой линзы
Между расстояниями от предмета до линзы и от линзы до изображения существует определенная зависимость от фокусного расстояния линзы, называемая формулой линзы.
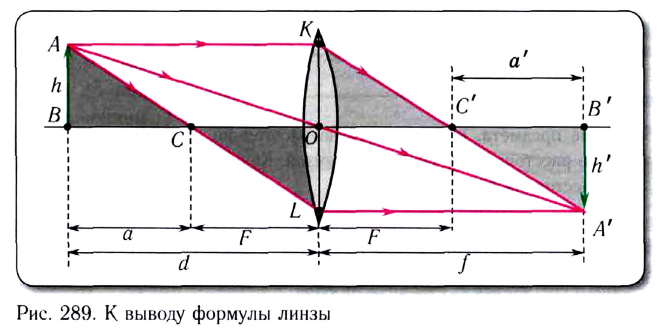
Выведем формулу тонкой линзы из геометрических соображений, рассматривая ход характерных лучей (рис. 289).
Пусть расстояние от предмета АВ до линзы d, расстояние от линзы до изображения АВ f, фокусное расстояние линзы F, расстояние от предмета до левого фокуса а, расстояние от изображения до правого фокуса а’.
Из рисунка видно, что 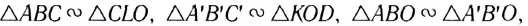
Поперечным увеличением Г называется отношение линейного размера изображения h’ к линейному размеру предмета h:

Из соотношения (I) следует формула Ньютона: 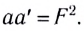
С учетом того, что 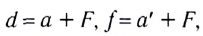
В 1604 г. в исследовании «Дополнения к Вителло» Кеплер изучал прелом-ление света в линзах различной конфигурации и для малых углов падения пришел к формуле линзы.
Для практического использования формулы линзы следует твердо запомнить правило знаков:
в случае собирающей линзы действительных источника и изображения величины F, d, f считают положительными; в случае рассеивающей линзы мнимых источника и изображения величины F, d, f считают отрицательными.
Заметим, что предмет или источник является мнимым только в том случае, если на линзу падает пучок сходящихся лучей.
Таким образом, линза с F>0 является собирающей (положительной), а с F 40 не применяются из-за сильных искажений изображения или малости обзора.
Мультимедийный (лазерный) проектор (рис. 292) — оптическое устройство, с помощью которого на экране получают действительное (прямое или обратное) увеличенное изображение, «снятое» с экрана компьютера, телевизора или других источников видеосигнала.
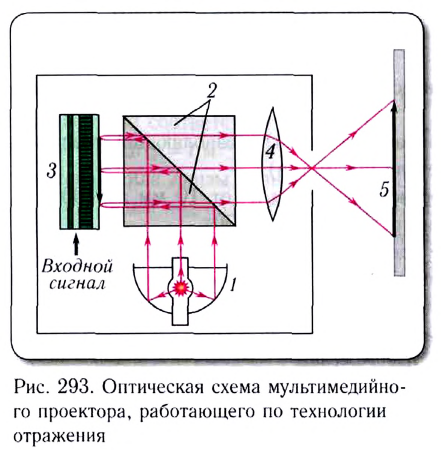
Для формирования изображения в мультимедиа-проекторах используются различные базовые технологии: жидкокристаллическая технология, технология цифровой обработки света или технология формирования цифровых изображений методом отражения.
При формировании цифрового изображения методом отражения источник света 1 при помощи разделяющих призм 2 освещает оптическую матрицу с изображением 3 и при помощи системы проекционных линз 4 передает увеличенное изображение на экран 5 (рис. 293).
Популярность мультимедийных проекторов обусловлен их универсальностью, поскольку помимо компьютерного изображения они поддерживают практически вес существующие стандарты видеозаписей, а также полностью совместимы с форматом телевидения высокой четкости.
Мультимедиа-проекторы активно работают на научных конференциях, вы-
семинарах и т. д., поскольку по размерам изображения и по возможностям его настройки с ними не способны конкурировать ни телевизоры, ни плазменные панели.
Так, например, мультимедиа-проекторы позволяют осуществить обратную проекцию или проекцию изображения на просветный экран, при которой зрители и проекционное оборудование находятся по разные стороны экрана. При такой установке проектора докладчик может находиться непосредственно перед экраном, не заслоняя собой проекцию, а освещение в помещении не так сильно влияет на качество изображения.
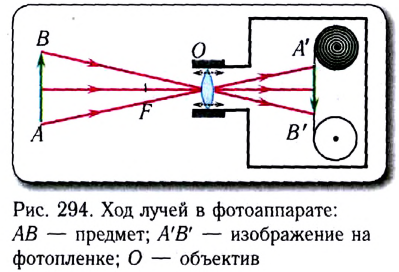
Фотоаппарат (рис. 294) — прибор, предназначенный для получения действительных уменьшенных обратных изображений предметов на фотопленке. При этом предметы могут быть расположены на различном удалении от точки съемки.
Фотоаппарат состоит из закрытой светонепроницаемой камеры и системы линз, называемых объективом (О). С помощью перемещения объектива добиваются наводки на резкость, при которой изображение предмета АВ формируется на фотопленке. В противном случае изображение А’В’ получается нечетким (размытым). Количество световой энергии, поступающей на пленку, определяется размерами диафрагмы и временем открытия затвора (выдержкой).
Сегодня на смену пленочным приходят электронные (цифровые) фотокамеры, в которых изображение записывается не на фотопленку, а на специальный чувствительный элемент (матрицу), с которого информация считывается и хранится в электронном (цифровом) виде, как в памяти компьютера. К достоинствам электронных камер можно отнести возможность «мгновенного» просмотра сделанной фотографии, восстановление ресурсов памяти после переписывания информации в компьютер, высокий темп съемки (10 и более кадров в секунду).
Зрение человека не в состоянии фиксировать очень быстрые и очень медленные изменения положения объекта. Фотоаппарат благодаря возможности фотографировать с различными выдержками от тысячных долей секунды до нескольких секунд позволяет хронометрировать события, визуально «неулавливаемые».
Глаз, очки
Основную часть информации (примерно 90 %) об окружающем мире мы получаем с помощью органов зрения.
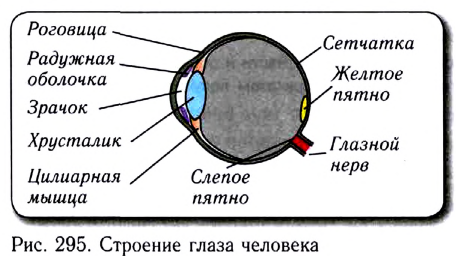
Глаз представляет собой сложную оптическую систему, подобную фотоаппарату (рис. 295).
Преломляющая система глаза подобна объективу фотоаппарата, а сетчатка — фоточувствительному слою фотопленки.
У глаза имеется радужная оболочка (окрашенная часть глаза), которая играет роль диафрагмы и автоматически регулирует количество попадающего в глаз света. Зрачок — отверстие в радужной оболочке, через которое проходит свет.
Сетчатка играет роль светочувствительной пленки, находится на задней поверхности глаза. Она состоит из «палочек» (нервные волокна) и «колбочек»
(рецепторы), которые преобразуют световую энергию в электрические сигналы, распространяющиеся по нервным волокнам. Днем свет воспринимается колбочками, а ночью — палочками. Днем мы отчетливо видим мелкие предметы и различаем их цвет. Слабо освещенные предметы (например, ночью) мы видим только в черно-белых тонах (бесцветными). Недаром говорят, что «ночью все кошки серы». Желтое пятно — область диаметром около 0,25 мм — находится в центре сетчатой оболочки, в которой достигается особая острота зрения и наиболее четко различаются цвета. Слепое пятно — место входа глазного нерва — это область сетчатки, которая не участвует в формировании изображения. Роговица — служит предохранительным покрытием и является первой поверхностью, преломляющей свет. Хрусталик — это эластичное линзоподобное тело, которое осуществляет настройку нашего зрения на различные расстояния. В оптической системе глаза фокусировка изображения на сетчатку называется аккомодацией (от латинского слова commodus — удобный). У человека аккомодация происходит за счет увеличения или уменьшения выпуклости хрусталика, которое осуществляется с помощью цилиарных мышц. При этом изменяется оптическая сила глаза.
Точка, видимая глазом при расслабленной цилиарной мышце, называется дальней точкой, а точка, видимая при максимальном напряжении этой мышцы, — ближней точкой.
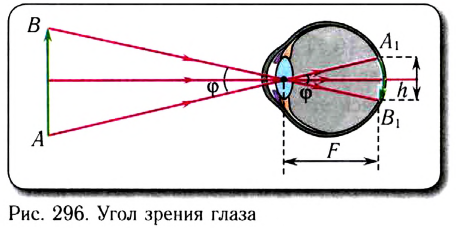
Расстояние наилучшего зрения — это расстояние от предмета до глаза, при котором глаз не устает и угол зрения достаточно велик. Размер изображения на сетчатке (рис. 296) определяется углом зрения 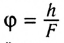
От бесконечно удаленного предмета в глаз попадает пучок параллельных лучей. В этом случае 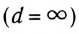
Оптическую силу аккомодационной добавки или аккомодации найдем из условия
Зрение человека с нормальным зрением характеризуется понятием «нормальный глаз», т. е. расстояние наилучшего зрения около 25 см, а предел зрения (дальняя точка) находится на бесконечности.
Для нормального глаза преломляющая сила хрусталика без аккомодации D= 19,11 дптр, а при максимальной аккомодации — 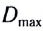
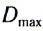
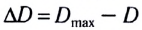
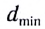
С возрастом возможность аккомодации быстро уменьшается в основном из-за уплотнения хрусталика, теряющего способность достаточно сжиматься. Пожилой человек не может отчетливо видеть близкие предметы, а также различать буквы в газетах и книгах. К пятидесяти годам расстояние наилучшего зрения увеличивается в среднем до 50 см.
С возрастом, по болезни или при несоблюдении гигиены могут появиться дефекты зрения. Два наиболее распространенных дефекта — близорукость и дальнозоркость.
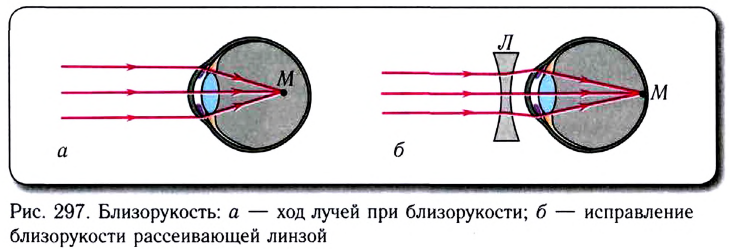
Близорукость (миопия) — дефект зрения, при котором глаз видит удаленные предметы не резко, а расплывчато (предел зрения не равен бесконечности). Изображения предметов при этом не попадают на сетчатку глаза, а фокусируются перед ней (точка М на рис. 297, а). Для исправления этого дефекта зрения используют очки с рассеивающими линзами (рис. 297, б). Поскольку оптическая сила этих линз отрицательна, то в повседневной жизни такие очки называют отрицательными.
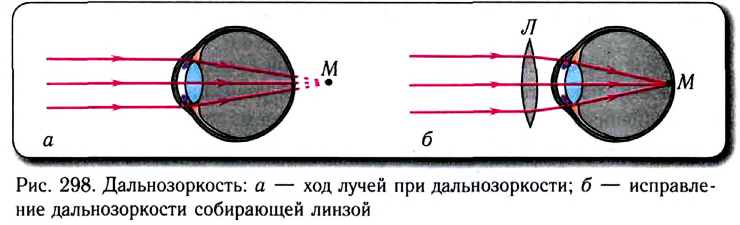
Дальнозоркость (гиперопия) — дефект зрения, при котором глаз не в состоянии видеть резко близкие объекты, хотя удаленные предметы он видит хорошо. Изображения предметов при дальнозоркости получаются за сетчаткой (точка Р на рис. 298, а), и для коррекции зрения необходимо применять собирающие линзы (рис. 298, б), оптическая сила которых положительна (положительные очки).
Оптические явления в атмосфере
Атмосфера нашей планеты представляет собой достаточно интересную оптическую систему, показатель преломления которой уменьшается с высотой вследствие уменьшения плотности воздуха. Таким образом, земную атмосферу можно рассматривать как «линзу» гигантских размеров, повторяющую форму Земли и имеющую монотонно изменяющийся показатель преломления.
Это обстоятельство приводит к появлению целого ряда оптических явлений в атмосфере, обусловленных преломлением (рефракцией) и отражением (реф-лекцией) лучей в ней.
Рассмотрим некоторые наиболее существенные оптические явления в атмосфере.
Атмосферная рефракция — явление искривления световых лучей при прохождении света через атмосферу.
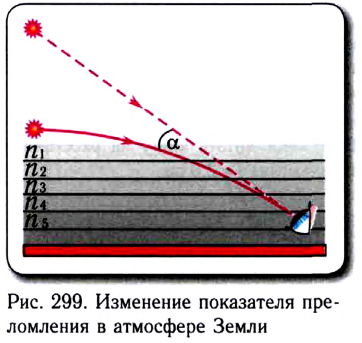
С высотой плотность воздуха (значит, и показатель преломления) убывает. Представим себе, что атмосфера состоит из оптически однородных горизонтальных слоев, показатель преломления в которых меняется от слоя к слою (рис. 299).
При распространении светового луча в такой системе он будет в соответствии с законом преломления «прижиматься» к перпендикуляру к границе слоя. Но плотность атмосферы уменьшается не скачками, а непрерывно, что приводит к плавному искривлению и повороту луча на угол а при прохождении атмосферы.
В результате атмосферной рефракции мы видим Луну, Солнце и другие звезды несколько выше того места, где они находятся на самом деле.
По этой же причине увеличивается продолжительность дня (в наших широтах на 10—12 мин), сжимаются диски Луны и Солнца у горизонта. Интересно, что максимальный угол рефракции составляет 35′ (для объектов у линии горизонта), что превышает видимый угловой размер Солнца (32′).
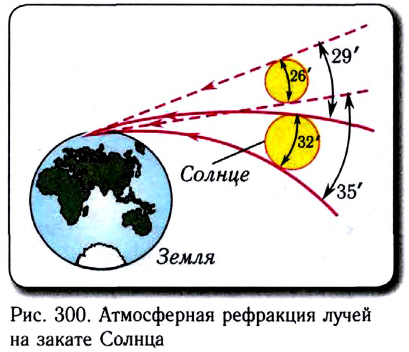
Из этого факта следует: в тот момент, когда мы видим, что нижний край светила коснулся линии горизонта, на самом деле солнечный диск находится уже под горизонтом (рис. 300).
Мерцание звезд также связано с астрономической рефракцией света. Давно было подмечено, что мерцание наиболее заметно у звезд, находящихся вблизи линии горизонта. Воздушные потоки в атмосфере изменяют плотность воздуха с течением времени, что приводит к кажущемуся мерцанию небесного светила. Космонавты, находящиеся на орбите, никакого мерцания не наблюдают.
В жарких пустынных или степных районах и в полярных областях сильный прогрев или охлаждение воздуха у земной поверхности приводит к появлению миражей: благодаря искривлению лучей становятся видимыми и кажутся близко расположенными предметы, которые на самом деле расположены далеко за горизонтом.
Иногда подобное явление называется земной рефракцией. Возникновение миражей объясняется зависимостью показателя преломления воздуха от температуры. Различают нижние и верхние миражи.
Нижние миражи можно увидеть в жаркий летний день на хорошо прогретой асфальтовой дороге: нам кажется, что впереди на ней есть лужи, которых на самом деле нет. В данном случае мы принимаем за «лужи» зеркальное отражение лучей от неоднородно разогретых слоев воздуха, находящихся в непосредственной близости от «раскаленного» асфальта.
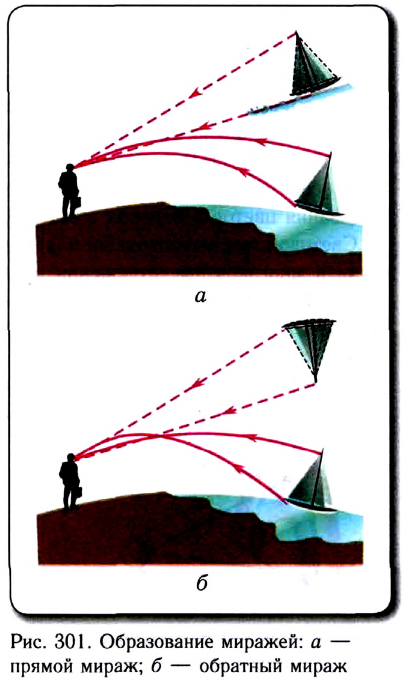
Верхние миражи отличаются значительным разнообразием: в одних случаях они дают прямое изображение (рис. 301, а), в других — перевернутое (рис. 301, б), могут быть двойными и даже тройными. Эти особенности связаны с различными зависимостями температуры воздуха и показателя преломления от высоты.
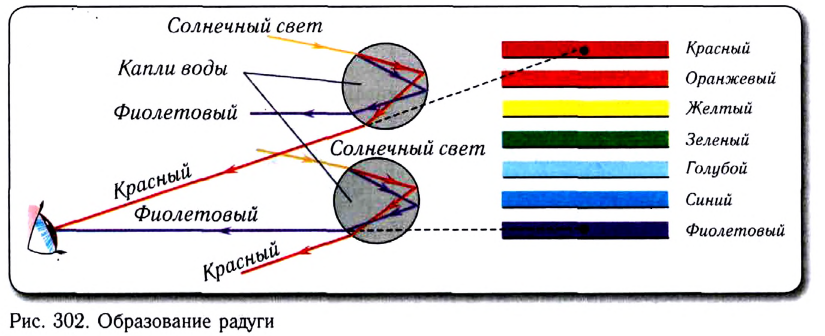
Атмосферные осадки приводят к появлению в атмосфере эффектных оптических явлений. Так, во время дождя удивительным и незабываемым зрелищем является образование радуги, которое объясняется явлением различного преломления (дисперсии) и отражения солнечных лучей на мельчайших капельках в атмосфере (рис. 302).
В особо удачных случаях мы можем увидеть сразу несколько радуг, порядок следования цветов в которых взаимообратен.
Световой луч, участвующий в формировании радуги, испытывает два преломления и многократные отражения в каждой дождевой капле. В данном случае, несколько упрощая механизм образования радуги, можем сказать, что сферические дождевые капельки играют роль призмы в опыте Ньютона по разложению света в спектр.
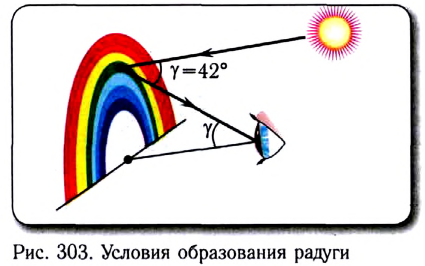
Вследствие пространственной симметрии радуга видна в виде полуокружности с углом раствора около 42°, при этом наблюдатель (рис. 303) должен находиться между Солнцем и каплями дождя, спиной к Солнцу.
Преломление света в кристалликах льда, сопровождающееся разложением в спектр, приводит к появлению сравнительно редкого и не менее красивого оптического явления гало (рис. 304).
Гало проявляется в виде кругов (иногда столбов, крестов) вокруг Солнца и Луны. Для появления яркого гало необходимо достаточное количество ледяных кристаллов правильной формы.
Разнообразие цветов в атмосфере объясняется закономерностями рассеяния света на частичках различных размеров. Вследствие того, что синий цвет рассеивается сильнее, чем красный, — днем, когда Солнце находится высоко над горизонтом, мы видим небо голубым. По этой же причине вблизи линии горизонта становится красным и не таким ярким, как в зените. Появление цветных облаков также связано с рассеянием света на частичках различных размеров в облаке.
Основные формулы в геометрической оптике
Предельный угол полного отражения: 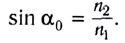
Формула тонкой линзы:
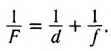
Оптическая сила линзы:
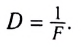
Поперечное увеличение:
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.