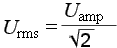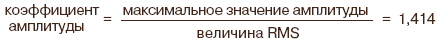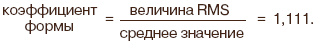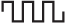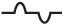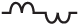что такое rms в электрике

Среднеквадратичное значение

Например, для чисел 2,3 и 6 среднеквадратичным значением будет квадратный корень из (2²+3²+6²)/3. √(49/3) = 4.04

Среднеквадратичным значением двух или нескольких чисел является квадратный корень из среднеарифметического значения квадратов этих чисел.

Среднеквадратичное значение применяется в расчётах, где существует пропорциональная зависимость не самих переменных значений, а их квадратов.

Действующее значение напряжения и тока

В качестве примера можно рассмотреть квадратичную зависимость мощности или работы электрического тока от значений тока или напряжения.

P = I²R; A = I²Rt; P = U²/R; A = U²t/R

Величина постоянного напряжения или тока является его среднеквадратичным значением.
Среднеквадратичное значение переменного тока равно величине постоянного тока, действие которого произведёт такую же работу в активной (резистивной) нагрузке за время периода.
Определяющим фактором здесь является среднее (среднеарифметическое) значение мощности P avg или работы A avg, пропорциональное квадрату значения тока.
Так же среднеквадратичное значение переменного напряжения за период равносильно по своему воздействию на активную нагрузку такому же значению постоянного напряжения.

Среднеквадратичное значение переменного напряжения или тока часто называют действующим или эффективным.

Примечание:
Электромагнитные приборы используют для измерения переменного тока и напряжения в промышленных установках. Усилие, создаваемое измерительной катушкой в электромагнитном приборе, пропорционально квадрату тока, поэтому не меняется по направлению.
Угол отклонения стрелки определится некоторым средним усилием F, которое будет пропорционально среднеквадратичному значению тока.

Расчёт действующего значения

В качестве примера рассчитаем среднеквадратичное значение синусоидального напряжения.

Запишем выражение U rms с применением интеграла функции U = U ampsin(t) для одного периода 2π :

Вынесем U amp из под знака радикала. Воспользуемся табличным интегралом , перепишем и решим последнее выражение с применением формулы Ньютона-Лейбница:

Так как sin(2π), sin(4π) и sin(0) равны нулю, вычисляем RMS синусоиды следующим образом:

В результате решения в итоге получим:

Расчёт RMS для напряжения или тока треугольной и пилообразной формы можно рассмотреть на примере одного периода T для функции , представленной на рисунке:

Выразим U rms искомой функции с помощью определённого интеграла:

Используя табличный интеграл и формулу Ньютона-Лейбница, получаем:

В итоге преобразований получим:

Для вариантов однополярного или двуполярного напряжения пилообразной и треугольной формы в периоде 2T или 4T, представленных на рисунке ниже, T и U amp имеют те же расчётные величины, что и в рассмотренном случае c функцией , а интегралы, определённые в интервалах, равных T, для квадратов используемых функций , будут иметь одно и то же значение

Следовательно, вышеуказанные варианты однополярного или двуполярного напряжения пилообразной и треугольной формы будут иметь среднеквадратичное значение .

В результате получаем значение RMS, равное произведению амплитуды импульсов U amp на квадратный корень из коэффициента заполнения (T i / T).

В качестве дополнительного материала предлагаем рассмотреть расчёт средеквадратичного значения напряжения накала кинескопа цветного телевизора, исходя из амплитуды и формы напряжения.

Замечания и предложения принимаются и приветствуются!

Источник

Важность использования RMS измерений для описания факторов, влияющих на качество электрической энергии

Каждый из нас слышал, что занятие письмом под шум прибоя может оказывать лечебный эффект.

Морские волны подобны синусоидальной волне переменного напряжения, которая используется в качестве эталонной при при определении качества питания. Отклонения от чисто синусоидальной формы волны могут быть обусловлены гармоническими составляющими, некратными гармониками, а также импульсными или колебательными переходными процессами. Изменения амплитуды синусоидального сигнала можно классифицировать следующим образом: падения, всплески и продолжительное перенапряжение либо пониженное напряжение. В то время как изменения в частоте питающего напряжения сравнительно редки и возникают при серьезных неполадках оборудования, чаще имеет место сдвиг фаз при провалах и всплесках. Для того чтобы охарактеризовать или описать синусоидальный сигнал, находящийся под воздействием описанных факторов, влияющих на качество электроэнергии, используются измерения истинных среднеквадратичных значений (Root Mean Squared — RMS). Являющиеся полезными во многих ситуациях, в ряде случаев такие измерения могут оказаться неадекватными либо вводить в заблуждение.

Что же представляют собой RMS?

Среднеквадратичные значения получаются в результате математической процедуры, используемой для расчета единичного значения по последовательности отсчетов. Это позволяет сравнивать один цикл с другим, или одну фазу с другой. RMS-напряжение является эффективным значением изменяющегося или переменного напряжения. Это значение должно соответствовать такой же мощности, как и в случае постоянного напряжения, приложенного к чистому сопротивлению. В нынешнем мире дискретных волновых сигналов, вырабатываемых кристаллами процессоров цифровой обработки сигнала (ЦОС), такие измерения являются одними из наиболее легко реализуемых. Каждое значение данных в течение предопределенного периода (обычно это один цикл) умножается само на себя (возведение в квадрат), а затем все такие значения в течение периода усредняются (суммируются с последующим делением на общее количество) и из полученного значения извлекается квадратный корень.

Для стабильного постоянного сигнала каждый отсчет имеет одно и то же значение, следовательно, любой из них может служить эквивалентом RMS-значения. В случае же синусоидальной волны значения нарастают в пределах первой четверти цикла, затем уменьшаются до нуля и переходят в область отрицательных значений вплоть до минимального значения в пределах второй четверти цикла (см. рис. 1).

Рисунок 1. Форма волны на нагрузке однофазного источника питания с полноволновым измерителем.

RMS-значение чистого синусоидального сигнала составляет примерно 70,7% пикового значения. При искаженной форме волны это не верно, что является ответом на вопрос, почему приборы, измеряющие не в терминах истинных среднеквадратичных значений, могут выдавать совершенно различные результаты при различных степенях искажений и, следовательно, не могут использоваться при наличии гармоник. Те приборы, которые лишь вычисляют 71% от пикового значения будут давать неверный результат для формы тока, показанного на рис. 1. На рисунке изображена классическая форма токового сигнала однофазного источника питания с выпрямлением полной волны, присутствующего во многих электронных устройствах. Эта форма волны с гармоническими искажениями (THD) на уровне 108% имела пиковое значение 3,6 А и истинное среднеквадратичное значение 1,4 А, что не совпадает с рассчитанной величиной 0,707×3,6=2,55 А.

Невысокого качества анализаторы электроэнергии, которые настроены на RMS-значения, могут пропускать некоторые данные. Ряд приборов рассчитывают RMS-значения в ходе нескольких циклов. Весьма вероятно, что эти мониторы не зафиксируют многофазовый провал в течение одного цикла, изображенный на рис. 2.

Рисунок 2. Провал в течение одного цикла в двух фазах.

Такое искажение сигнала типично для случая, когда неполадка устраняется с помощью защитного предохранителя. На рис. 3 провал в течение одного цикла, возникший вследствие пробоя при пиковом напряжении (возможно из-за неисправности изоляции или удара молнии) будет давать различные RMS-значения на каждом из трех циклов.

Рисунок 3. Однофазный провал при пробое пиковым напряжением.

В зависимости от механизма включения триггера и пороговых значений, возможно необнаружение провала вплоть до третьего цикла, поскольку RMS-значение неисправных циклов может превышать порог срабатывания триггера. Неисправность, выражающаяся в сдвиге фаз, может иметь идентичные значения от одного цикла к следующему, несмотря на изменения амплитуды волны. Это происходит, когда используются электроанализаторы со многими механизмами включения триггера, например при переходных процессах или искажениях формы волны. Следует помнить, что хотя прибор не замечает таких неисправностей, это не значит, что они не существуют.

Справка

Консультативно-торговая компания «Энергометрика» поставляет компоненты автоматизации для: АСУ ТП, «интеллектуальное» здание, шкаф электрический, конденсаторная установка, системы учета параметров электроэнергии. SCADA системы.

Источник

Истинное RМS – единственно правильное измерение

Во многих коммерческих и промышленных установках происходят постоянные отключения защитных систем. Зачастую отключения кажутся случайными и необъяснимыми, но, конечно, причина существует, а в нашем случае их две. Первая возможная причина – это противотоки, которые возникают при включении некоторых видов нагрузки, например персональных компьютеров (этот вопрос будет рассмотрен в одной из будущих публикаций данного руководства). Второй возможной причиной является то, что реальный ток, протекающий по цепи, был недоизмерен, т. е. реальные значения тока выше измеренного.

Один ток – два значения. На фото показано измерение цепи с нелинейной нагрузкой с гармоническими искажениями. Показания измерителя истинного RMS (слева) правильны, а измерителя усредненных значений (справа) – на 32 % ниже.

Занижение значений измерения случается очень часто в современных установках. Но почему это происходит, если современные цифровые измерительные приборы так точны и надежны? Ответ заключается в том, что многие инструменты не подходят для измерения искаженных токов, а большинство токов в наши дни являются таковыми.

Искажения происходят из-за гармонических токов, производимых нелинейными нагрузками, особенно электронным оборудованием, таким как персональные компьютеры, флуоресцентными лампами с электронным балластом и регулируемым приводом. Процесс возникновения гармоник, а также их воздействие на электрические системы будет описываться в одной из будущих публикаций руководства (раздел 3.1). На рис. 3 изображена типичная кривая тока, потребляемого персональным компьютером. Очевидно, что это не синусоида, а стало быть все обычные синусоидные измерительные приборы и методы вычисления больше не применимы. Это означает, что при ремонте или анализе работы системы электроснабжения необходимо использовать приборы, которые могут измерять несинусоидальные токи и напряжения.

На рис. 1 изображены два измеряющих прибора (токовые клещи) на одной и той же цепи. Оба прибора работают правильно и откалиброваны по спецификациям производителя. Ключевое различие заключается в том, как измеряют данные инструменты.

Левый прибор является устройством измерения истинного RMS, а правый – это калиброванный прибор, измеряющий усредненный RMS. Для того чтобы оценить разницу, необходимо понять, что означает RMS.

Что такое RMS?

Среднеквадратичная величина (RMS) переменного тока – это величина, эквивалентная значению постоянного тока, который производил бы такое же количество теплоты при фиксированной нагрузке. Количество теплоты, производимой в резисторе переменным током, пропорционально квадрату тока, усредненного по полному циклу кривой. Другими словами, производимая теплота пропорциональна среднему значению квадрата, и, таким образом, величина тока пропорциональна корню среднеквадратичного значения (полярность не имеет значения, т. к. квадрат всегда положителен).

Типичная кривая тока, потребляемого персональным компьютером

Для правильной синусоиды (рис. 2) величина RMS составляет 0,707 от максимального значения, или максимальное значение равно √2, или 1,414, от значения RMS. То есть максимальное значение 1-амперного RMS тока чистой синусоиды будет равно 1,414 А. Если амплитуда синусоиды усредняется (с преобразованием отрицательной половины цикла), среднее значение будет равно 0,636 от максимального или 0,9 от значения RMS. На рис. 2 показаны две важных пропорции:

При измерении правильной синусоиды (и только для правильной синусоиды) правомерно делать простое измерение среднего значения (0,636 х максимум) и умножать результат на коэффициент формы, равный 1,111 (что составит 0,707 от максимума), и назвать его RMS-величиной. Подобный подход используется в аналоговых измерительных приборах, где усреднение осуществляется путем инерции и гашения колебаний в катушке индуктивности, а также во всех старых и более современных цифровых универсальных измерительных приборах. Метод описывается как измерение, усредненное, RMS-калиброванное.

Проблема заключается в том, что этот метод работает только для правильных синусоид, которые не существуют в реальных электроустановках. Кривая на рис. 3 – это типичная кривая тока, потребляемого персональным компьютером. Точное RMS-значение все еще равно 1 А, но максимальное значение гораздо выше – 2,6 А, а среднее значение гораздо ниже – 0,55 А.

Если эта кривая измеряется усредняющим RMS-прибором, то она будет читаться как 0,61 А, в то время как реальная величина равна 1 А (т. е. почти на 40 % меньше). В таблице приведены некоторые примеры того, как два различных типа измерителей реагируют на различные формы волн.

В измерителе истинного RMS берется квадрат моментальной величины входящего тока, усредняется по времени, а затем на дисплее показывается квадратный корень от этого среднего значения. При идеальных условиях применения показания абсолютно точны, какая бы ни была кривая. Однако применение никогда не бывает идеальным, и следует принимать во внимание два ограничивающих фактора: частотную характеристику и коэффициент амплитуды.

Для функционирования систем электроснабжения обычно достаточно произвести измерения до 50-й гармоники, т. е. до частоты приблизительно в 2 500 Гц. Максимальное значение амплитуды, пропорция между максимальным значением и RMS-значением очень важны. Более высокие значения максимальной амплитуды требуют приборы с более широким динамическим диапазоном, а следовательно, более высокой точности в преобразовании диаграммы.

Несмотря на то что приборы дают различные показания при измерени искаженных кривых, показания обоих приборов совпадут при измерении правильной синусоиды. Это условие, при котором они калибруются, т. е. каждый тип измерительного прибора может быть сертифицирован как калиброванный, но только для использования на синусоидах.

Счетчики истинного RMS появились по крайней мере 30 лет назад, но они были специализированными и относительно дорогими приборами. Достижения в электронике привели к тому, что функции истинного RMS-измерения встраиваются во многие переносные мультиметры. К сожалению, эта техническая характеристика встречается только в наиболее современных продуктах большинства производителей, но при этом они не так дороги, как раньше, и стали доступными инструментами для использования в повседневной деятельности.

Таблица Сравнение реакций на различные формы волн измерителей усредненного и истинного RMS

Тип измерения мультиметра Реакция на синусоиду Реакция на прямоуголь- ное колебание Реакция на однофазный диодный выпрямитель Реакция на трехфазный диодный выпрямитель Усредненное RMS Правильная На 10 % выше На 40 % ниже На 5–30 % ниже Истинное RMS Правильная Правильная Правильная Правильная

Последствия заниженного замера

Эксплуатационные ограничения большинства элементов электрической цепи определяются количеством тепла, которое может быть рассеяно с тем, чтобы элемент или компонент не перегрелся.

Номиналы допустимых значений тока для кабелей, к примеру, приводятся для определенных условий эксплуатации (фактор, определяющий, насколько быстро может происходить отвод тепла) и максимальной допустимой рабочей температуры. Так как гармонически загрязненные токи имеют большее значение RMS, чем то, которое замеряется счетчиком усредненного RMS, примененные провода и кабели могут иметь недостаточные номиналы и будут работать более нагретыми, чем ожидалось. Результатом будет разрушение изоляции, преждевременный износ и опасность пожара.

Размерность шины измеряется путем подсчета соотношения скорости охлаждения конвекцией и излучения, а также скорости нагрева из-за потерь сопротивления. Температура, при которой эти скорости равны, является рабочей температурой шины, или она спроектирована так, чтобы рабочая температура была достаточно низкой для избежания преждевременного износа изоляционных и опорных материалов. Как и в случае с кабелями, ошибки при измерении истинного RMS-значения приведут к более высоким рабочим температурам. Вследствие того что шины обычно имеют значительные размеры, поверхностный эффект более очевиден, чем в маленьких проводниках.

Это приводит к еще большему увеличению температуры.

Другие компоненты электрической системы, такие как плавкие предохранители и тепловые элементы автоматов отключения оцениваются в токе RMS, потому что их характеристики имеют отношение к рассеиванию теплоты. Это является основной причиной раздражающих псевдоаварийных отключений – сила тока выше ожидаемой, поэтому автомат отключения функционирует в температурном режиме, при котором отключения будут происходить неминуемо. Как при любом перерыве в подаче электроэнергии, стоимость сбоя из-за аварийного отключения может быть довольно высокой и повлечь за собой потерю данных в компьютерных системах, сбои в работе систем управления технологическими процессами и т. д. Эти вопросы будут обсуждаться в будущих публикациях руководства (раздел 2)

Таким образом, только с помощью инструментов измерения истинного RMS возможен точный выбор номиналов кабелей, шин, фидеров и защитной аппаратуры. Важным является вопрос, является ли данное устройство прибором измерения истинного RMS? Обычно, если счетчик является измерителем истинного RMS, это указывается в спецификации продукта. Практически ответ может быть получен путем сравнения показаний известного усредняющего измерителя (как правило, самого дешевого, который может быть в распоряжении) и предполагаемого измерителя истинного RMS при замере тока в нелинейной нагрузке, например, тока от персонального компьютера с током лампы накаливания. Оба измерителя покажут одинаковую силу тока для нагрузки лампы накаливания. Если один из приборов имеет значительно более высокие показатели (скажем на 20 % выше) для нагрузки персонального компьютера, чем для другой нагрузки, тогда, вероятно, он является прибором истинного RMS, а если показания одинаковы – приборы относятся к одному и тому же типу.

Заключение

RMS-замеры важны для любой установки, в которой имеется значительное число нелинейных нагрузок (персональные компьютеры, электронные балласты, компактные флуоресцентные лампы и т. д.). Усредняющие RMS-измерители дают недомер до 40 %, что приводит к недооценке номиналов кабелей и защитных устройств. Это грозит сбоями в их работе, аварийными отключениями и преждевременным износом.

Нелишне помнить и о том, что при функционировании в режимах нерасчетной электрической и, главное, тепловой нагрузки, вызванной недооценкой истинных значений токов в результате недомера, снижается общая энергоэффективность электроустановки.

Перепечатано с сокращениями из издания Европейского института меди

«Прикладное руководство по качеству электроэнергии»

Источник

Бюджетный вариант измерения TrueRMS

Измерение trueRMS переменного напряжения — задача не совсем простая, не такая, какой она кажется с первого взгляда. Прежде всего потому, что чаще всего приходится измерять не чисто синусоидальное напряжение, а нечто более сложное, усложнённое наличием гармоник шумов.

Поэтому соблазнительно простое решение с детектором среднего значения с пересчётом в ср.кв. значения не работает там, где форма сигнала сильно отличается от синусоидальной или просто неизвестна.

Профессиональные вольтметры ср. кв. значения — это достаточно сложные устройства как по схемотехнике, так и по алгоритмам [1,2]. В большинстве измерителей, которые носят вспомогательный характер и служат для контроля функционирования, такие сложности и точности не требуются.

Также требуется, чтобы измеритель мог быть собран на самом простом 8-битном микроконтроллере.

Общий принцип измерения

Пусть имеется некое переменное напряжение вида, изображённого на рис. 1.

Квазисинусоидальное напряжение имеет некий квазипериод T.

Преимущество измерения среднеквадратичного значения напряжения в том, что в общем случае время измерения не играет большой роли, оно влияет только на частотную полосу измерения. Большее время даёт большее усреднение, меньшее даёт возможность увидеть кратковременные изменения.

Базовое определение ср. кв. значения выглядит вот таким образом:

где u(t) — мгновенное значение напряжения
T — период измерения

Таким образом, время измерения может быть, вообще говоря, любым.

Для реального измерения реальной аппаратурой для вычисления подинтегрального выражения необходимо проквантовать сигнал с некоторой частотой, заведомо превосходящей не менее, чем в 10 раз частоту квазисинусоиды. При измерении сигналов с частотами в пределах 20 кГц это не представляет проблемы даже для 8-битных микроконтроллеров.

Другое дело, что все стандартные контроллеры имеют однополярное питание. Поэтому измерить мгновенное переменное напряжение в момент отрицательной полуволны не представляется возможным.

В работе [3] предложено довольно остроумное решение, как внести постоянную составляющую в сигнал. Вместе с тем в том решении определение момента, когда стоит начать или закончить процесс вычисления ср. кв. значения представляется довольно громоздким.

В данной работе предлагается метод преодоления этого недостатка, а также вычисление интеграла с большей точностью, что позволяет снизить число точек выборки до минимума.

Особенности аналоговой части измерителя

На рис. 2 показано ядро схемы предварительной аналоговой обработки сигнала.

Сигнал поступает через конденсатор C1 на усилитель-формирователь, собранный на операционном усилителе DA1. Сигнал переменного напряжения замешивается на неинвертирующем входе усилителя с половиной опорного напряжения, которое используется в АЦП. Напряжение выбрано 2.048 В, поскольку в компактных устройствах часто используется напряжение питания +3.6 В и менее. В иных случаях удобно использовать 4.048 В, как в [3].

С выхода усилителя-формирователя через интегрирующую цепочку R3-C2 сигнал поступает на вход АЦП, который служит для измерения постоянной составляющей сигнала (U0). C усилителя-формирователя сигнал U’ — это измеряемый сигнал, сдвинутый на половину опорного напряжения. Таким образом, чтобы получить переменную составляющую, достаточно вычислить разность U’-U0.
Сигнал U0 используется также в качестве опорного для компаратора DA2. При переходе U’ через значение U0 компаратор вырабатывает перепад, который используется для формирования процедуры прерывания для сбора измерительных отсчётов.

Важно, что во многие современные микроконтроллеры встроены как операционные усилители, так и компараторы, не упоминая АЦП.

На рис. 3 дан базовый алгоритм для случая измерения величины переменного напряжения с основной частотой 50 Гц.

Запуск измерения может осуществляться по любому внешнему событию вплоть до кнопки, нажимаемой вручную.

После запуска в первую очередь измеряется постоянная составляющая во входном сигнале АЦП, а затем контроллер переходит в ожидание положительного перепада на выходе компаратора. Как только прерывание по перепаду наступает, контроллер делает выборку из 20 точек с временным шагом, соответствующим 1/20 квазипериода.

В алгоритме написано X мс, поскольку низкобюджетный контроллер имеет собственное время задержки. Чтобы измерение происходило в правильные моменты времени, необхоимо учитывать эту задержку. Поэтому реальная задержка будет меньше 1 мс.

В данном примере задержка соответствует измерениям квазисинусоид в диапазоне 50 Гц, но может быть любой в зависимости от квазипериода измеряемого сигнала в пределах быстродействия конкретного контроллера.

При измерениях ср.кв. значения напряжения произвольного квазипериодического сигнала, если априори неизвестно, что это за сигнал, целесообразно измерить его период, используя встроенный в контроллер таймер и тот же выход компаратора. И уже на основании этого замера устанавливать задержку при осуществлении выборки.

Вычисление среднеквадратичного значения

После того, как АЦП создал выборку, имеем массив значений U'[i], всего 21 значение, включая значение U0. Теперь, если применить формулу Симпсона (точнее, Котеса) для численного интергрирования, как наиболее точную для данного применения, то получим следующее выражение:

где h — шаг измерения, а нулевой компонент формулы отсутствует, поскольку он равег 0 по определению.

В результате вычисления мы получим значение интеграла в чистом виде в формате отсчётов АЦП. Для перевода в реальные значения полученное значение нужно промасштабировать с учётом величины опорного напряжения и поделить на интервал времени интегрирования.

где Uоп — опорное напряжение АЦП.

Если всё пересчитать в мВ, K приблизительно равняется просто 2. Масштабный коэффициент относится к разностям в квадратных скобках. После пересчёта и вычисления S делим на интервал измерения. С учётом множителя h фактически получаем деление на целое число вместо умножения на h с последующим делением на интервал времени измерения.

И в финале извлекаем квадратный корень.

И вот тут самое интересное и сложное наступает. Можно, разумеется, использовать плавающую точку для вычислений, поскольку язык C это допускает даже для 8-битных контроллеров, и производить вычисления непосредственно по приведённым формулам. Однако скорость расчёта упадёт существенно. Также можно выйти за пределы весьма небольшого ОЗУ микроконтроллера.

Чтобы такого не было, нужно, как верно указано в [3], использовать фиксированную точку и оперировать максимум 16-битными словами.

Автору эту проблему удалось решить и измерять напряжение с погрешностью Uоп/1024, т.е. для приведённого примера с точностью 2 мВ при общем диапазоне измерения ±500 мВ при напряжении питания +3.3 В, что достаточно для многих задач мониторинга процессов.

Программная хитрость состоит в том, чтобы все процессы деления, по возможности, делать до процессов умножения или возведения в степень, чтобы промежуточный результат операций не превышал 65535 (или 32768 для действий со знаком).

Конкретное программное решение выходит за рамки данной статьи.

В данной статье рассмотрены особенности измерения среднеквадратичных значений напряжения с помощью 8-битных микроконтроллеров, показан вариант схемной реализации и основной алгоритм получения отсчётов квантования реального квазисинусоидального сигнала.

Источник