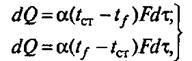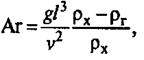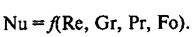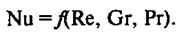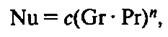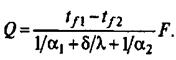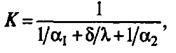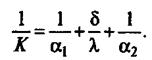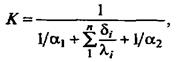что собой представляет коэффициент теплоотдачи

Что собой представляет коэффициент теплоотдачи

Коэффициент теплопередачи является количественной расчет ной величиной и зависит от коэффициентов теплоотдачи, термического сопротивления стенки и загрязнений.

Для плоской стенки

, (9.28)

где – коэффициент теплоотдачи от горячего теплоносителя, Вт/(м град); – толщина теплопередающей стенки аппарата, м; — коэффициент теплопроводности материала стенки, Вт/(м град); — коэффициент теплоотдачи от стенки к холодному теплоносителю, Вт/(м град); – термическое сопротивление загрязнения стенки, м 2 град/Вт.

Если теплопроводность слоя загрязнения неизвестна, подсчитывают К для чистой стенки, а влияние загрязнения стенки учитывают при помощи коэффициента использования поверхности теплообмена j

, (9.29)

Коэффициенты теплоотдачи a определяются в основном из формул

или

где Nu – безразмерный критерий подобия Нуссельта; l – коэффициент теплопроводности теплоносителя (для которого определяется коэффициент теплоотдачи), Вт/(м град); l – определяющий геометрический размер, м; – эквивалентный диаметр, м.

(9.31)

где F – площадь поперечного сечения потока, м 2 ; П – смоченный периметр, м.

Критерий Нуссельта в зависимости от состояния и характера движения сред определяется по различным критериальным уравнениям.

Для подсчета a ₁ и a ₂ критериальное уравнение выбирается по справочникам так, чтобы оно возможно точно совпадало с условиями расчета.

Для устойчивого турбулентного режима движения жидкостей внутри труб ( Re > 10000) рекомендуется следующее критериальное уравнение:

, (9.32)

где – критерий Рейнольдса; – критерий Прандтля; — средняя скорость теплоносителя, м/с; l – определяющий геометрический размер, м; r – плотность теплоносителя, кг/м; m – вязкость теплоносителя, Н с/м 2 ; – массовая скорость теплоносителя, кг/(м ₂ с); – эквивалентный диаметр, м; c – удельная теплоемкость теплоносителя, Дж/(кг град); l – теплопроводность теплоносителя, Вт/(м град).

Здесь за определяющую температуру принята , а за определяющий размер эквивалентный диаметр . Уравнение (8.32) применяется при , 100 > Pr > 0,6; для труб – при условии , где l – длина трубы, м; d – диаметр трубы, м.

, (9.33)

Для ламинарного движения ( Re

, (9.34)

где a – множитель (для горизонтальных труб d = 0,74; для вертикальных труб a= 0,85), – критерий Грасгофа; g = 9,81 ускорение свободного падения, м/с 2 ; r – плотность теплоносителя, кг/м ; b – коэффициент объемного расширения теплоносителя, град –1 ; – частный температурный напор, град.

Если теплоноситель перемещается в межтрубном пространстве (при наличии перегородок), то критерий Нуссельта определяется по уравнению

, (9.35)

Источник

Коэффициент теплоотдачи поверхность — воздух

В статье рассмотрен расчет мощности теплового потока от горизонтальных и вертикальных плоских поверхностей тела, помещенного в «безразмерное» воздушное пространство при принудительной и естественной конвекции с учетом радиационной составляющей теплоотдачи.

Зная коэффициент теплоотдачи на поверхности (α), разделяющей твердое тело и окружающее это тело воздушное пространство, очень просто определить мощность теплового потока (Q) по известной разности температур (Δt).

Q=α*A*Δt, Вт – мощность теплового потока от или к поверхности тела.

Основная сложность расчета заключается в определении коэффициента конвективной теплоотдачи (α_к)! Автоматизировать в первую очередь решение этой трудоемкой задачи поможет Excel.

Нестабильность процесса естественной конвекции у поверхностей различной формы и расположения в пространстве породила большое разнообразие эмпирических формул для вычисления коэффициента конвективной теплоотдачи (α_к). Неизбежные погрешности экспериментальных данных привели к тому, что результаты вычислений для одних и тех же поверхностей и условий по формулам разных авторов отличаются друг от друга на 20% и более.

После тщательного детального ознакомления с материалами современных западных изданий по теплообмену (список литературы – в конце статьи) были выбраны формулы, рекомендованные к применению большинством авторов, для использования в представленной далее программе в Excel.

Схемы теплообмена:

На представленных ниже рисунках показаны 8 вариантов схем, для которых программа может выполнить вычисления.

Розовый цвет пластин свидетельствует о том, что они горячее окружающего воздуха. Голубой цвет – пластины холоднее воздуха.

На схемах 1а и 1б воздух принудительно движется (вентилятор, ветер) вдоль поверхности пластины независимо от её ориентации в пространстве. На всех остальных схемах окружающий воздух находится в спокойном состоянии (помещение, полный штиль), а положение пластин сориентировано в пространстве.

Расчет в Excel:

Формулы алгоритма программы:

t₀=(t_в+t_п)/2

l₀=L – для схем 1а и 1б

l₀=(B*L)/(2*(B+L)) – для схем 2а, 2б, 3а, 3б, 4а, 4б

Re=w*l₀/ν

Gr=g*β*|t_п— t_в|*l₀ 3 /ν 2

Ra=Gr*Pr

α_к=Nu*λ/l₀

α_р=ε*0,00000005670367*((t_п+273,15) 4 — (t_в+273,15) 4 )/(t_п-t_в)) – при t_в *) α_р=0 – при t_в>t_п

α=α_к+α_р

q=α*(t_п-t_в)

Q=q*B*L

*) Нагрев поверхностей Солнцем или иными источниками теплового излучения программой игнорируется.

Вычисление теплофизических параметров воздуха и числа Нуссельта, как видно из вышеприведенных формул, являются ключевыми и самыми трудоемкими при определении конвективного коэффициента теплоотдачи.

Тестирование программы проводилось на примерах из книг, представленных в конце статьи. Отклонения результатов в основном не выходили за пределы ±5%.

Замечание:

В отечественной теплотехнической литературе для решения рассмотренных задач широко используются формулы второй половины прошлого века М.А. Михеева и В.П. Исаченко, которые в современной западной литературе не упоминаются. Беглый сравнительный анализ результатов расчетов по формулам разных авторов дал противоречивые и неоднозначные ответы. Если при принудительной конвекции результаты фактически идентичны, то при естественной конвекции отличаются порой на 30% и более, но иногда почти совпадают…

Литература:

Прошу уважающих труд автора скачать файл с программой после подписки на анонсы статей!

P. S. (01.11.2020)

Дополнение по естественной конвекции у вертикальной поверхности:

Если построить графики по вышеприведенным формулам Черчилля и Чу для числа Нуссельта при естественной конвекции у вертикальной изотермической поверхности (схемы 2а и 2б), то можно увидеть, что при Ra=10 9 кривые не совпадают!

Еще один нюанс, который встретился только у Линхардов в [1]: «свойства флюида следует оценивать при t₀=(t_в+t_п)/2 за одним исключением, если флюид – газ, то коэффициент объемного расширения β следует определять при t₀=t_в». Но сами авторы зависимостей Черчилль и Чу о таком условии ничего не пишут. По этому поводу в их статье [7], говорится, что «для больших температурных перепадов, когда физические свойства существенно различаются, Ид рекомендует оценивать физические свойства как средние значения температуры поверхности и объема, а Уайли дает более подробные теоретические указания для режима ламинарного пограничного слоя».

Правы Линхарды или множество других авторов, рассчитывающих все свойства флюидов при одном значении определяющей температуры t₀=(t_в+t_п)/2? Однозначного ответа у меня нет.

(По материалам Обри Джаффера [8].)

Эмпирические уравнения для суммарного коэффициента теплоотдачи:

В инженерных расчетах для быстрого приближенного определения суммарного коэффициента теплоотдачи, учитывающего и конвекцию, и излучение на границе поверхность тела – среда, можно использовать более простые зависимости, приведенные в [9].

При расчете тепловых потерь через наружные поверхности тел, которые находятся в спокойном воздухе закрытых помещений, можно применить нижеприведенные формулы. Результаты вычислений по этим формулам достаточно близки к результатам более точных расчетов.

α=9,74+0,07*(t_п-t_в), Вт/(м2*°C) при t_п On-line калькуляторы для расчетов коэффициентов конвективной теплоотдачи от плоских, цилиндрических и сферических поверхностей:

Инструменты представлены Группой исследований теплопередачи (HTRG). Группа была создана в 2014 году преподавателями Лаборатории теплотехники и жидкостей факультета машиностроения инженерной школы Сан-Карлоса (EESC) Университета Сан-Паулу (USP) для проведения передовых, качественных фундаментальных и прикладных исследований по вопросам теплопередачи для многофазных и однофазных систем.

Точность результатов вычислений не проверял.

Источник

ВОПРОС № 1 Теоретические основы теплоотдачи

Конвективный теплообмен

1. Г.Д. Кавецкий, В.П. Касьяненко «Процессы и аппараты пищевой технологии».- М., КолосС, 2008.-591 с.: ил.

1. Теоретические основы теплоотдачи.

2. Связь коэффициента теплопередачи с коэффициентами теплоотдачи.

1. Дайте определения и краткую характеристику существа процесса теплоотдачи?

2. В чем сущность основного закона теплоотдачи – закона Ньютона?

3. Какие критерии, характеризующие процесс теплоотдачи Вам известны?

4. Что каждый из них характеризует?

ВОПРОС № 1 Теоретические основы теплоотдачи

Теплоотдачей называется процесс теплообмена между поверх­ностью тела и окружающей средой.

Интенсивность теплоотдачи характеризуется коэффициентом теплоотдачи, равным отношению плотности теплового потока на поверхности раздела к температурному напору между поверхностью теплообмена и средой (теплоносителем).

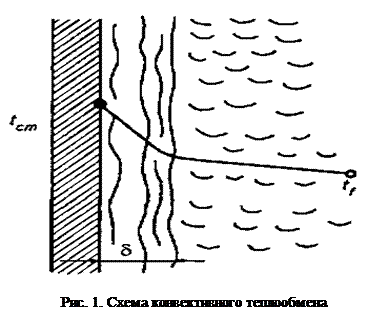
При конвективном теплообмене теплота распространяется в потоке жидкости или газа от поверхности твердого тела или к его поверхности одновременно конвекцией и тепло­проводностью. От поверхности твер­дого тела к потоку жидкости она рас­пространяется через пограничный слой за счет теплопроводности, от по­граничного слоя к ядру потока жидко­сти или газа — в основном конвекци­ей. На интенсивность теплоотдачи су­щественное влияние оказывает характер движения потока жидкости или газа. Схема конвективного теплообмена приведена на рис. 1. Различают теплоотдачу при свободной и вынужденной конвек­ции. Под свободной, или естественной, конвекцией понимают перемещение частиц жидкости или газа в объеме аппарата или теплообменных устройств вследствие разности плотностей нагре­тых и холодных частиц жидкости или газа.

Скорость естественной конвекции определяется физическими свойствами жидкости или газа, разностью температур между горячими и холодными части­цами и объемом, в котором протекает процесс.

Вынужденная, или принудительная, конвекция возникает под действием насоса или вентилятора и определяется физическими свойствами среды, скоростью ее движения, формой и размерами канала, в котором движется поток.

При вынужденной конвекции теплообмен происходит значи­тельно интенсивнее, чем при естественной.

Основной закон теплоотдачи — закон Ньютона гласит: количе­ство теплоты dQ, переданное от поверхности теплообмена к пото­ку жидкости (газа) или от потока к поверхности теплообмена, прямо пропорционально площади поверхности теплообмена F, разности температур поверхности t_ст и ядра потока t_f (или наобо­рот) и продолжительности процесса dτ:

Единицу измерения коэффициента теплоотдачи можно получить, решив уравнения (1):

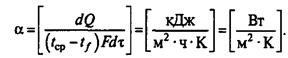
Если коэффициент теплоотдачи имеет постоянное значение вдоль всей поверхности теплообмена (а = const), уравнения (1) принимают вид

(3)

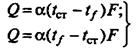
в зависимости от того, передается теплота от стенки омывающему стенку потоку или наоборот.

Значение коэффициента теплоотдачи, который определяет скорость конвективного теплообмена, зависит от многих факто­ров: режима движения жидкости (газа), физических параметров жидкости (газа), формы и размера поверхности теплообмена и др.

Коэффициент теплоотдачи рассчитывают по критериальных уравнениям, которые получают методами теории подобия из диф­ференциального уравнения конвективного теплообмена, допол­ненного уравнениями, характеризующими условие на границе раздела потока и стенки аппарата.

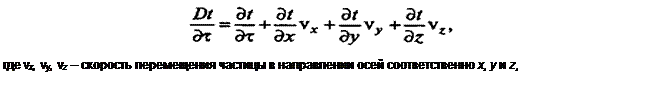Дифференциальное уравнение конвективного теплообмена (урав­нение Фурье—Кирхгофа) получают, приравняв субстанциональную производную * (4)

к уравнению (6):

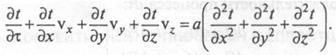
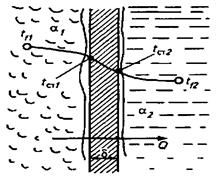
Для полного математического описания процесса последнее уравнение требуется дополнить условиями на границе раздела по­тока и стенки аппарата. Для этого рассмотрим процесс конвектив­ного теплообмена между стенкой аппарата и потоком жидкости (см. рис. 1). В данном случае поток жидкости можно рассмат­ривать как двухслойную систему, состоящую из пограничного слоя толщиной δ и ядра потока, в котором происходит интенсив­ное перемешивание частиц жидкости при турбулентном режиме.

Теплота от стенки аппарата через пограничный слой распростра­няется теплопроводностью, которая описывается законом Фурье [уравнение (5)]. Это же количество теплоты, описываемое зако­ном Ньютона, распространяется в ядре пото­ка. Приравнивая эти уравнения, получим уравнение, характеризу­ющее условия на границе,

(6)

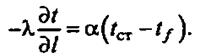
* Субстанциональная производная выражает изменение температуры элемента одновременно во времени и в пространстве, связанное с перемещением элемента из одной точки в другую.

Дифференциальные уравнения, однако, можно привести к рас­четному виду только в простейших случаях. Во всех остальных случаях расчетные уравнения получают, используя методы теории подобия, из общих дифференциальных уравнений, приводя их при помощи экспериментальных данных к конкретному виду.

Критерий Нуссельта, характеризующий условия на границе, можно получить методами теории подобия из уравнения (6). Для этого делят обе части уравнения (6) на его левую часть и получают безразмерный комплекс

(7)

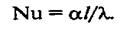
откуда после несложных преобразований — критерий Нуссельта

(8)

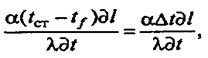
Критерий Фурье выводят из дифференциального уравнения конвективного теплообмена (5):

(9)

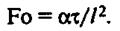
Критерий Фурье характеризует связь между скоростью измене­ния температурного поля, размерами канала, в котором происхо­дит теплообмен, и физическими свойствами среды в нестационар­ных условиях.

Критерий Пекле

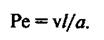
Критерий Пекле показывает соотношение между количеством теплоты, распространяемой в потоке жидкости или газа конвек­цией, и теплопроводностью.

Легко видеть, что критерий Пекле представляет собой произве­дение критериев Рейнольдса и Прандтля

Ре = Vl/a = (Vl/v)(v/a) = RePr, (11)

где υ – кинематическая вязкость, м 2 /с.

Критерий Прандтля характеризует поле теплофизических вели­чин потока жидкости или газа

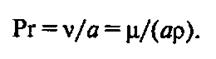
Учитывая, что коэффициент температуропроводности а = λ/сρ, критерий Прандтля записывается в виде Рг=μс/λ

При теплообмене в условиях естественной конвекции в крите­риальные уравнения вводят критерии Грасгофа

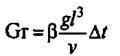
Из приведенных критериев подобия только критерий Нуссель­та содержит искомый коэффициент теплоотдачи, не входящий в условия однозначности, поэтому он является определяемым кри­терием подобия.

Критериальное уравнение конвективного теплообмена в общем виде

При стационарном процесса теплообмена из критериального уравнения (15) исключает критерий Фурье.

При вынужденной конвекции из критериального уравнения исключают критерий Грасгофа

При естественной конвекции из критериального уравнения ис­ключают критерий Рейнольдса

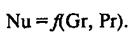
К расчетному виду уравнения (15), (17) и (18) приводят на основании экспериментальных данных, полученных в конкрет­ной гидродинамической и геометрической обстановке.

Коэффициент теплоотдачи определяют по найденному из кри­териальных уравнений критерию Нуссельта.

Коэффициент теплоотдачи при естественной конвекции рассчи­тывают на основе критериального уравнения.

в котором числовые значения сипвыбирают в зависимости от произведения GrPr:

Определяющей температурой в критерии Грасгофа является средняя температура пограничного слоя t= 0,5(t_cт + t_f),а Δt= t_cт – t.

Коэффициент теплоотдачи при вынужденной конвекции теплоно­сителя в трубе определяют по следующим уравнениям:

для турбулентного режима (Re > 10 000)

(20)

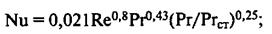
для ламинарного режима (Re ≤ 2320)

При поперечном обтекании трубы теплоносителем при Rе = (10÷2)∙10 5 используют уравнение

(22)

В котором числовые значения с и п находят в зависимости от значения критерия Рейнольдса:

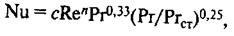
Определяющим размером в этих уравнениях служит эквивалент­ный диаметр канала.

Физические параметры в критериях Nu, Re и Рr определены при средней температуре жидкости, а в критерии Рr_ст — при тем­пературе стенки.

(Рr/Рr_ст) 0,25 учитывает влияние на теплоотдачу направления теплового потока и температурного перепада.

При расчете коэффициента теплоотдачи в змеевиках значение α, полученное по формуле (20), умножают на коэффициент χ, учитывающий размеры змеевика:

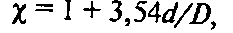
где d, D – соответственно внутренний диаметр трубы змеевика и диаметр витка змеевика, м.

Для воздуха формула (20) имеет вид

(24)

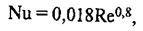
так как в этом случае Pr\Pr_ст=1.

Когда теплота распространяется одновременно конвекцией и лучеиспусканием, в расчётное уравнение вводят общий коэффициент теплоотдачи α_общ= α_к+ α_изл, где α_к – конвективный коэффициент теплоотдачи; α_изл – коэффициент теплоотдачи излучением:

(25)

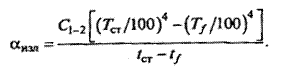
Для определения общего коэффициента теплоотдачи [Вт/(м 2 · К)] при расчете тепловых потерь аппаратуры, находящейся в закрытых помещениях, можно пользоваться приближенным уравнением

(26)

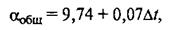
где Δt – разность температур поверхности стенки аппарата и окружающей среды.

ВОПРОС № 2 Связь коэффициента теплопередачи с коэффициентами теплоотдачи

Коэффициент теплопередачи рассчитывают на основании коэффициентов теплоотдачи, вычисленных по критериальным уравнениям.

Рис. 2. К расчету процесса теплопередачи

При установившемся процессе количество теплоты Q, передаваемое в единицу времени через площадку F от ядра потока горячего тепло­носителя стенке, равно количеству теплоты, передаваемому через стенку теплопроводностью и от стенки ядру потока холодного теплоносителя. Это количество теплоты можно определить:

Из этих уравнений получают разности температур или частные температурные напоры.

Складывая, левые и правые части этих уравнений, получают разность температур теплоносителей, или общий температурный напор

Из сопоставления уравнений и (40) получают

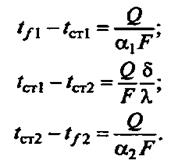
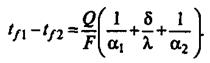
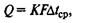
Величина 1/К, обратная коэффициенту теплопередачи, называ­ется общим термическим сопротивлением теплопередачи и обо­значается R(R= r₁+ + r_ст + r₂).

Величины l/α₁ и 1/α₂ называются частными термическими со­противлениями r₁ и r₂, а δ/λ — термическим сопротивлением стен­ки r_ст. Из уравнения (42) следует, что общее термическое со­противление теплопередаче равно сумме частных термических со­противлений теплоотдаче теплоносителей и стенки.

В случае многослойной стенки в уравнение (42) вместо δ/λ подставляют сумму термических сопротивлений каждого слоя стенки. Тогда

где п — число слоев стенки; і—порядковый номер слоя.

Отметим, что коэффициент теплопередачи всегда меньше ми­нимального коэффициента теплоотдачи.

Источник